补码的乘法-布斯乘法

前言

本篇文章讲解如何通过逻辑门的形式来实现补码的乘法操作

布斯乘法

A.D.Booth提出了一种补码相乘算法,可以将符号位与数值位合在一起参与运算，直接得出用补码表示的乘积，且正数和负数同等对待。这种算法被称之为Booth (布斯)乘法
下面有两个变量值$X$、$Y$
$Y$用二进制表示为
$Y=y_{n?1}{y}_{n?2}\dots y_2{y}_1{y}_0$
因为Y是用补码表示的，所以Y的值可以通过下面的公式计算：
$$\begin{array}{rl}Y& =?y_{n?1}{2}^{n?1}+y_{n?2}{2}^{n?2}+\dots +y_1{2}^1+y_0{2}^0\\ & =?y_{n?1}{2}^{n?1}+\sum _{i=0}^{n?2}{y}_i{2}^i\\ & =?y_{n?1}{2}^{n?1}+y_{n?2}{2}^{n?1}?y_{n?2}{2}^{n?2}+\dots +y_1{2}^2?y_1{2}^1+y_0{2}^1?y_0\\ & =(y_{n?2}?y_{n?1})2^{n?1}+(y_{n?3}?y_{n?2})2^{n?2}+\dots +(y_0?y_1)2^1+(0?y_0)\\ & =\sum _{i=0}^{n?1}(y_{i?1}?y_i)2^i\end{array}$$
因为$X$、$Y$都是n位数据，所以$X\times Y$可能占用2n位。
我们先假设$Y$乘以$2^{?n}$
$$\begin{array}{rl}X\times Y\times 2^{?n}& =X\times \sum _{i=0}^{n?1}(y_{i?1}?y_i)2^i\times 2^{?n}\\ & =X\times \sum _{i=0}^{n?1}(y_{i?1}?y_i)2^{?(n?i)}\\ & =P_n\end{array}$$
即然我们假设这个值等于$P_n$了，那么我们可以推测$P_{n?1}$的值
$$P_{n?1}=X\times \sum _{i=0}^{n?2}(y_{i?1}?y_i)2^{?(n?1?i)}$$
然后我们能得出两个挨着的一般性公式$P_i$和$P_{i?1}$的关系
$$P_i=2^{?1}(P_{i?1}+(y_{i?2}?y_{i?1})X)，i=1,2\dots ,n?1$$

根据上面的公式，我们发现，可以先计算$P_0$，然后通过$P_0$计算$P_1$，然后通过$P_1$计算$P_2$，然后就可以依次往后计算出$P_n$，如果计算$X\times Y$，我们可以按照下面的步骤进行：

1. 假设$P_0=0$，假设$y_{?1}=0$
2. 从y的最右侧位开始，先比较$y_0$和$y_{?1}$
3. 如果$y_0{y}_{?1}==00$，$P_0$右移一位
4. 如果$y_0{y}_{?1}==01$，$P_0+X$然后，右移一位
5. 如果$y_0{y}_{?1}==10$，$P_0?X$然后，右移一位
6. 如果$y_0{y}_{?1}==11$，$P_0$右移一位
7. 右移后得到$P_1$，比较位向左移动一位，如果没有超过最大位，跳转到2
8. 如果超过最高位了，$P_n$就是结果

注意：在此之前，其实$P_n=X\times Y\times 2^{?n}$，并且我们发现在上述步骤中结果一直在向右移，所以，我们可以把初始结果放在高n位上，这样向右移动不会丢失数据，并且也相当于乘了$2^n$，结果刚好是想要的值。

通过上面的步骤可以看出，乘法被分解成一系列加减和移位操作的顺序集合，我们之前已经实现了串行进位加法器和并行进位加法器，并且实现了一个桶形移位器

下面看一个实际的例子：
假设X = 100，Y = 120；
用二进制表示为X = 01100100，Y= 01111000，即然8位能够放下数据，为了书写方便，我们假设XY都为8位，结果为16位数据，假设结果为R = 0；

1. 比较$y_0$与$y_{?1}$,$y_0{y}_{?1}=00$，R=00000000 00000000，右移后值不变
2. 比较$y_1$与$y_0$,$y_1{y}_0=00$，R=00000000 00000000，右移后值不变
3. 比较$y_2$与$y_1$,$y_2{y}_1=00$，R=00000000 00000000，右移后值不变
4. 比较$y_3$与$y_2$,$y_3{y}_2=10$，R=00000000 00000000，R-X后右移
   R-X = R(高位) + (~X) + 1= 10011100 00000000，右移后为11001110 00000000
   注意：是在R的高位上操作，并且右移为算数右移，补符号位
5. 比较$y_4$与$y_3$,$y_4{y}_3=11$，R=11001110 00000000，右移后为11100111 00000000
6. 比较$y_5$与$y_4$,$y_5{y}_4=11$，R=11100111 00000000，右移后为11110011 10000000
7. 比较$y_6$与$y_5$,$y_6{y}_5=11$，R=11110011 10000000，右移后为11111001 11000000
8. 比较$y_7$与$y_6$,$y_7{y}_6=01$，R=11111001 11000000，R+X后右移，R+X = 01011101 11000000， 右移后为00101110 11100000

计算完成，00101110 11100000 = 12000，与结果相符

布斯乘法在电路的实现

我们在前面讲述算法执行过程的时候，把结果数据放在了高n位，这样有两个好处：

• 正好抵消了之前公式中乘的$2^{?n}$
• 在算法执行过程中结果数据总要右移，把结果数据放在高位，右移的时候不会丢失数据

并且每一步我们都会从右往左比较Y的位值，相当于我们每步都右移Y，然后比较Y的最低两位，但是第一步的时候我们还有一个$y_{?1}=0$，所以我们可以这么设计：

• 假设Y有n位，我们设计的电路有n+1根线，Y的值放在$n～1$位，$y_{?1}$的值放在0位
• 这样，每一步的比较操作我们只需要右移电路一位，然后比较最低的两位值即可

即然结果数据和Y的值都右移，并且每步骤都右移1位，那么我们可以设计一个通用的电路：

• 假设Y有n位，我们设计的电路有2n+1位，数据结果保存到$2n～n+1$位，Y的值放在$n～1$位，$y_{?1}$的值放在0位
• 最终的结果就是高2n位的数据

下面给出电路图：

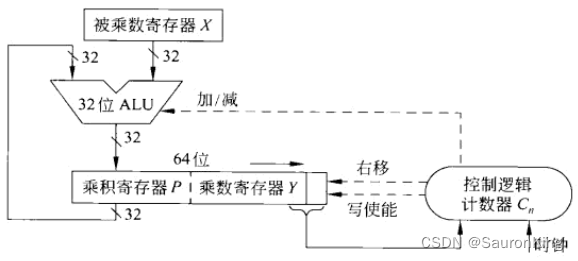
图中表示的是32位的布斯乘法电路图，电路的执行步骤如下：

• 我们假设乘积寄存器P+乘数寄存器Y+最右边保存$y_{?1}$的值统称为R。
• 默认乘积寄存器P的值为0，最右边保存$y_{?1}$的值为0，乘数寄存器Y的值和被乘数寄存器X的值被输入，计数器为0，时钟用来增加计数器的值
• 每一步时钟，检查R的第两位，根据值的不同执行不同的电路逻辑
  • 00或者11，R右移，执行下一步
  • 01，执行加法操作，结果保存到乘积寄存器P，R右移，执行下一步
  • 10，执行减法操作，结果保存到乘积寄存器P，R右移，执行下一步
• 计数器等于32，输出结果乘积寄存器P+乘数寄存器Y，结束

算术一位右移

虽然我们实现了桶形移位器，但是在当前的乘法运算中，有点大材小用，如果我们仅仅实现一个一位的右移操作，电路将变得很简单，我们直接给出C语言描述git地址

/**
 * 单位右移操作，为了实现布斯乘法专门定义的右移电路，支持129位
 * in_1：128～65位，用于存放乘积寄存器P
 * in_2：64～1位，用于存放乘数寄存器Y
 * in_1：0位，用于存放临时比较的值
 * isLogic：是否是逻辑右移
 */
extern void alu_shift_right_1(long* in_1,long*  in_2,long*  in_3,long isLogic);

void alu_shift_right_1(long* in_1,long* in_2,long*  in_3,long isLogic)
{
    // 先赋值最低位
    *in_3 = (*in_2)&1;
    // in_1的最低位给in_2的最高位
    unsigned long a = *in_2;
    *in_2 = (a>>1)| ((*in_1)&1)<<(sizeof(long)*8-1);
    // in_1右移1位
    if(isLogic)
    {
        unsigned long b = *in_1;
        *in_1 = b>>1;
    }
    else
    {
        *in_1 = (*in_1)>>1;
    }
}

布斯乘法的C语言描述

最后给出布斯乘法的C语言描述，我们把结果存在两个long类型的数值中，out_1保存高位，out_2保存低位。git地址

/**
 * 使用布斯乘法算法计算两个数相乘
 * in_1：输入1
 * in_2：输入2
 * out_1：输出高位
 * out_2：输出低位
 */
extern void alu_booth_times(long in_1, long in_2,long* out_1, long* out_2);

void alu_booth_times(long in_1, long in_2,long* out_1, long* out_2)
{
    // y-1位,默认为0
    long lastBit = 0;
    // 保存结果的高位
    *out_1 = 0;
    long c = 0;
    // 计数器
    for(int i = 0; i<sizeof(long)*8;i++)
    {
        long temp = in_2&1;
        if(temp == lastBit)// 直接右移
        {
            alu_shift_right_1(out_1,&in_2,&lastBit,0);
        }
        else if(lastBit==1)// 01,相加，然后右移
        {
            c = 0;
            *out_1 = alu_add_bcla_64(*out_1,in_1,sizeof(long)*8,&c);
            alu_shift_right_1(out_1,&in_2,&lastBit,0);
        }
        else// 10,相减，然后右移
        {
            *out_1 = alu_sub_bcla_64(*out_1,in_1,sizeof(long)*8);
            alu_shift_right_1(out_1,&in_2,&lastBit,0);
        }
    }
    *out_2 = in_2;
}