并查集测试

1.介绍

**本质：**处理一些不相交的集合的合并问题，**比如：**最小生成树，最近公共祖先
操作： 1.初始化init，2.find查询，3.合并union

2.初始化init()

将父节点零散的散开->父节点为本身fa[i]=i，fa[i]=i相当于i的祖先是本身（同时作为find的递归结束条件）

int fa[MAX]
void init(int n){
  for(int i=1;i<=10;i++){
    fa[i]=i;//设置每个节点的父节点
  }
}

3.find()查找祖先节点

过程： 1.base：当前节点的祖先为本身时结束if(fa[i]==i) ——>2.否则不断向上递归寻找父节点 return find(fa[i])

   int find(int i){ //寻找i的祖先节点
      if(fa[i]==i){ //base
       return i;
      }else{
       return find(fa[i]);
      }
   
   }

4.合并union()

过程： 1. 本质就是得到i的祖先与j的祖先——> 2.然后使i的祖先的祖先 为 j的祖先

  void union(int i,int j){
    int fa_i=find(i); //1.得到i节点的祖先
    int fa_j=find(j); //2.得到j节点的祖先
    fa[fa_i]=fa_j; //3.使i节点的祖先的祖先指向j的祖先
  }

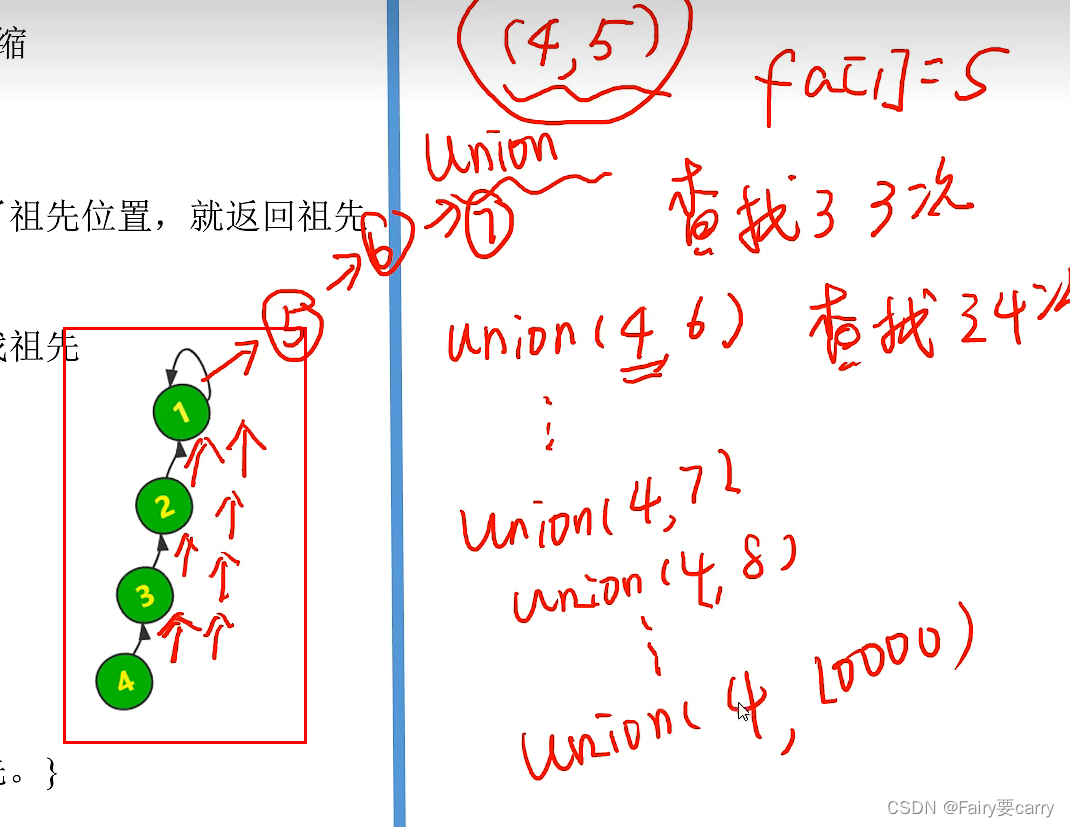
5.路径压缩

缺点： find递归的时候对子链条进行重复计算 ，普通递归如果链条上为四个节点，那么find一个节点最差需要四次，相反若是路径压缩后，则需要一次

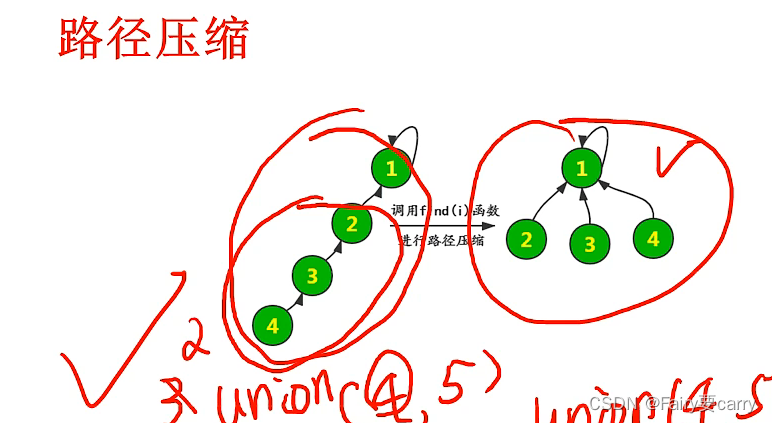
int find(int i){
  if(fa[i]==i){
  return i; //base:当遍历到祖先节点，自己就是自己的祖先 
  }
  fa[i]=find(fa[i]); //说明i为子树节点，将i的祖先指向它祖先的祖先
  return fa[i]; 
}

案例

#include<stdio.h>
#include<stdlib.h>
#define MAXN 1000
int fa[MAXN];

//1.初始化父节点
void init(int n){
	for(int i=1;i<=n;i++){
		//1.1初始化当前节点的父节点为本身
		fa[i]=i;
	}
}

int find(int x){
	//1.base找到祖先节点=自身节点结束
	if(fa[x]==x) return x;
	else{
		//2.路径压缩，只需寻找一次就能够找到x的祖先节点
     fa[x]=find(fa[x]);
	 return fa[x];
	}
}

//3.合并节点
void unionn(int i,int j){
	//1.首先find节点i和j的祖先节点
	int i_fa=find(i);
	int j_fa=find(j);
	//2.i的祖先的祖先为j的祖先
	fa[i_fa]=j_fa;
}

int main(){
	int number;//人员数量
	int relations; //关系数量
	int first,second;//建立关系的两个temp节点
	int s=1;
	
	printf("请输入人员数量:\n");
	scanf("%d",&number);
	init(number);
	printf("人员初始化成功...\n");
	
	printf("请输入关系个数:\n");
	scanf("%d",&relations);
	for(int i=1;i<=relations;i++){
		printf("输入两个节点，初始化关系..\n");
		scanf("%d,%d",&first,&second); //输入两个节点
		unionn(first,second); //建立关系first->second
	}
	
	
	while(s){
		//1.查询两个节点是否隶属于同一个祖先
		printf("请输入两个节点：\n");
	    scanf("%d,%d",&first,&second);
	    if(find(first)==find(second)){
			//2.相同祖先
			printf("%d和%d是属于同一个祖先\n",first,second);
		}
		s=0;
	}
	
	
	
}