梯度爆炸实验

造成简单循环网络较难建模长程依赖问题的原因有两个：梯度爆炸和梯度消失。一般来讲，循环网络的梯度爆炸问题比较容易解决，一般通过权重衰减或梯度截断可以较好地来避免；对于梯度消失问题，更加有效的方式是改变模型，比如通过长短期记忆网络LSTM来进行缓解。

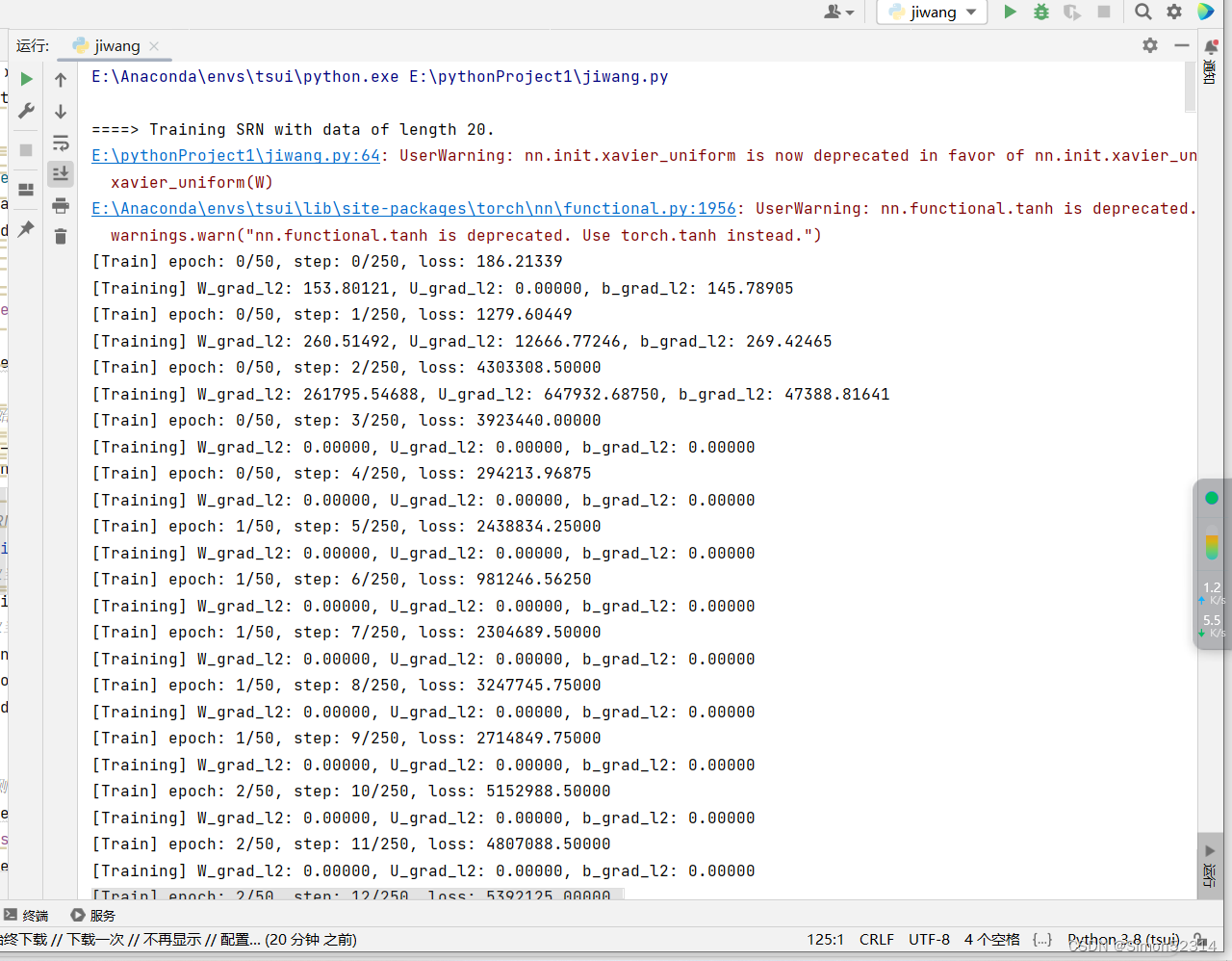
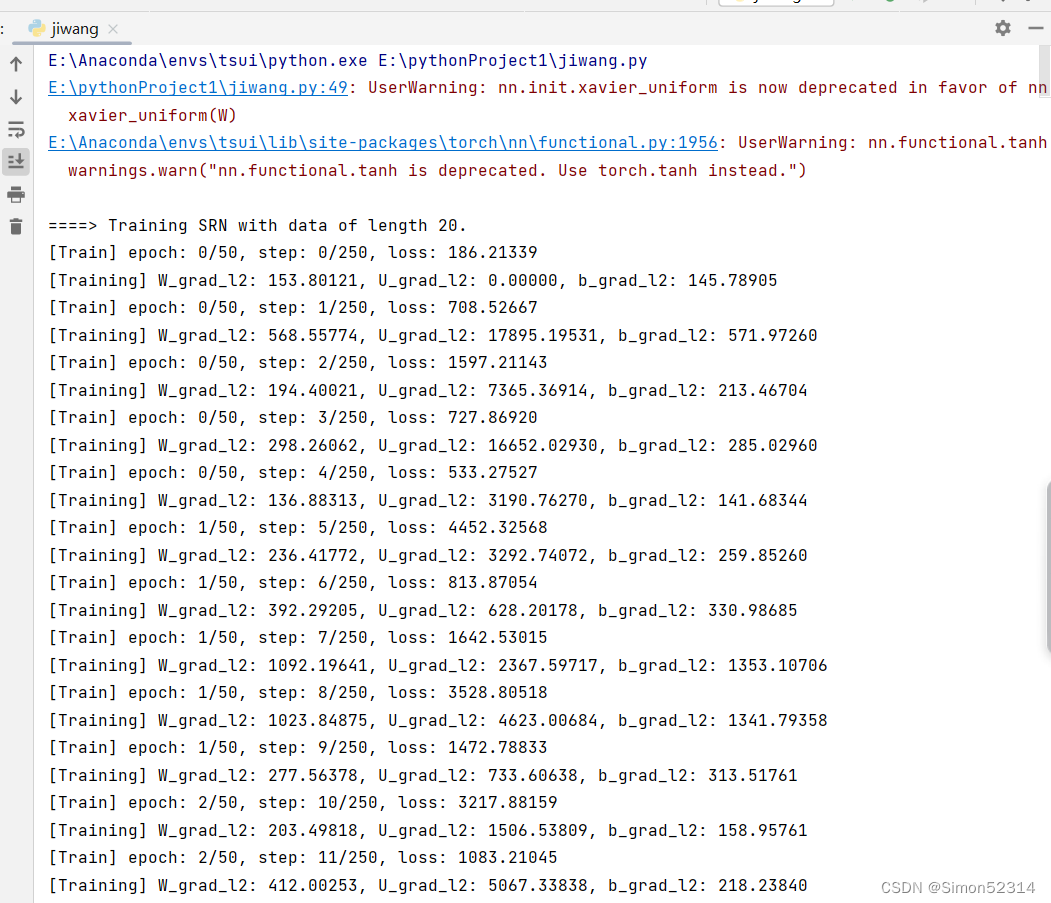
本节将首先进行复现简单循环网络中的梯度爆炸问题，然后尝试使用梯度截断的方式进行解决。这里采用长度为20的数据集进行实验，训练过程中将进行输出W,U,b的梯度向量的范数，以此来衡量梯度的变化情况。

6.2.1 梯度打印函数

使用custom_print_log实现了在训练过程中打印梯度的功能，custom_print_log需要接收runner的实例，并通过model.named_parameters()获取该模型中的参数名和参数值. 这里我们分别定义W_list, U_list和b_list，用于分别存储训练过程中参数W,U和bW,U和b的梯度范数。
?

import torch

W_list = []
U_list = []
b_list = []
# 计算梯度范数
def custom_print_log(runner):
    model = runner.model
    W_grad_l2, U_grad_l2, b_grad_l2 = 0, 0, 0
    for name, param in model.named_parameters():
        if name == "rnn_model.W":
            W_grad_l2 = torch.norm(param.grad, p=2).numpy()[0]
        if name == "rnn_model.U":
            U_grad_l2 = torch.norm(param.grad, p=2).numpy()[0]
        if name == "rnn_model.b":
            b_grad_l2 = torch.norm(param.grad, p=2).numpy()[0]
    print(f"[Training] W_grad_l2: {W_grad_l2:.5f}, U_grad_l2: {U_grad_l2:.5f}, b_grad_l2: {b_grad_l2:.5f} ")
    W_list.append(W_grad_l2)
    U_list.append(U_grad_l2)
    b_list.append(b_grad_l2)

【思考】什么是范数，什么是L2范数，这里为什么要打印梯度范数？?

什么是范数？

我们知道距离的定义是一个宽泛的概念，只要满足非负、自反、三角不等式就可以称之为距离。范数是一种强化了的距离概念，它在定义上比距离多了一条数乘的运算法则。有时候为了便于理解，我们可以把范数当作距离来理解。

在数学上，范数包括向量范数和矩阵范数，向量范数表征向量空间中向量的大小，矩阵范数表征矩阵引起变化的大小。一种非严密的解释就是，对应向量范数，向量空间中的向量都是有大小的，这个大小如何度量，就是用范数来度量的，不同的范数都可以来度量这个大小，就好比米和尺都可以来度量远近一样；对于矩阵范数，学过线性代数，我们知道，通过运算AX=B，可以将向量X变化为B，矩阵范数就是来度量这个变化大小的。

例如：1比2小我们一目了然，可是（3,5,3）和（6,1,2）哪个大？不太好比吧
2范数比：根号（43）比根号（41）大，因此2范数对比中（3,5,3）大
无穷范数比：5比6小，因此无穷范数对比中（6,1,2）大

矩阵范数：描述矩阵引起变化的大小，AX=B，矩阵X变化了A个量级，然后成为了B。
向量范数：描述向量在空间中的大小。
更一般地可以认为范数可以描述两个量之间的距离关系。

向量范数的通用公式为L-P范数

记住该公式其他公式都是该公式的引申。
L-0范数：用来统计向量中非零元素的个数。
L-1范数：向量中所有元素的绝对值之和。可用于优化中去除没有取值的信息，又称稀疏规则算子。
L-2范数：典型应用——欧式距离。可用于优化正则化项，避免过拟合。
L-∞范数：计算向量中的最大值。

这里为什么要打印梯度范数？??

当梯度过大时，它可能导致模型训练过程中的数值不稳定，进而影响模型的性能。

在梯度爆炸实验中，打印范数可以帮助我们了解梯度的幅度大小。范数可以衡量向量的大小，因此通过打印梯度的范数，我们可以直观地看到梯度的幅度是否过大或过小。

如果梯度的范数过大，这可能意味着模型在训练过程中出现了问题，例如梯度爆炸。在这种情况下，我们可以采取一些措施来解决问题，例如调整学习率、使用梯度裁剪等。

简单说，就是范数可以反应梯度的大小，打印范数我们可以及时知道梯度的情况。

?6.2.2 复现梯度爆炸现象

为了更好地复现梯度爆炸问题，使用SGD优化器将批大小和学习率调大，学习率为0.2，同时在计算交叉熵损失时，将reduction设置为sum，表示将损失进行累加。 代码实现如下：

from torch.utils.data import Dataset
from torch.nn.init import xavier_uniform
import torch.nn as nn
import torch.nn.functional as F
import os
import random
import torch
import numpy as np
from nndl4.metric import Accuracy
from nndl4.runner import RunnerV3
W_list = []
U_list = []
b_list = []
# 计算梯度范数
def custom_print_log(runner):
    model = runner.model
    W_grad_l2, U_grad_l2, b_grad_l2 = 0, 0, 0
    for name, param in model.named_parameters():
        if name == "rnn_model.W":
            W_grad_l2 = torch.norm(param.grad, p=2).numpy()
        if name == "rnn_model.U":
            U_grad_l2 = torch.norm(param.grad, p=2).numpy()
        if name == "rnn_model.b":
            b_grad_l2 = torch.norm(param.grad, p=2).numpy()
    print(f"[Training] W_grad_l2: {W_grad_l2:.5f}, U_grad_l2: {U_grad_l2:.5f}, b_grad_l2: {b_grad_l2:.5f} ")
    W_list.append(W_grad_l2)
    U_list.append(U_grad_l2)
    b_list.append(b_grad_l2)
class DigitSumDataset(Dataset):
    def __init__(self, data):
        self.data = data

    def __getitem__(self, idx):
        example = self.data[idx]
        seq = torch.tensor(example[0], dtype=torch.int64)
        label = torch.tensor(example[1], dtype=torch.int64)
        return seq, label

    def __len__(self):
        return len(self.data)
class Embedding(nn.Module):
    def __init__(self, num_embeddings, embedding_dim,
                 para_attr=xavier_uniform):
        super(Embedding, self).__init__()
        # 定义嵌入矩阵
        W=torch.zeros(size=[num_embeddings, embedding_dim], dtype=torch.float32)
        self.W = torch.nn.Parameter(W)
        xavier_uniform(W)
    def forward(self, inputs):
        # 根据索引获取对应词向量
        embs = self.W[inputs]
        return embs
# 加载数据
def load_data(data_path):
    # 加载训练集
    train_examples = []
    train_path = os.path.join(data_path, "train.txt")
    with open(train_path, "r", encoding="utf-8") as f:
        for line in f.readlines():
            # 解析一行数据，将其处理为数字序列seq和标签label
            items = line.strip().split("\t")
            seq = [int(i) for i in items[0].split(" ")]
            label = int(items[1])
            train_examples.append((seq, label))
    # 加载验证集
    dev_examples = []
    dev_path = os.path.join(data_path, "dev.txt")
    with open(dev_path, "r", encoding="utf-8") as f:
        for line in f.readlines():
            # 解析一行数据，将其处理为数字序列seq和标签label
            items = line.strip().split("\t")
            seq = [int(i) for i in items[0].split(" ")]
            label = int(items[1])
            dev_examples.append((seq, label))
    # 加载测试集
    test_examples = []
    test_path = os.path.join(data_path, "test.txt")
    with open(test_path, "r", encoding="utf-8") as f:
        for line in f.readlines():
            # 解析一行数据，将其处理为数字序列seq和标签label
            items = line.strip().split("\t")
            seq = [int(i) for i in items[0].split(" ")]
            label = int(items[1])
            test_examples.append((seq, label))
    return train_examples, dev_examples, test_examples
# SRN模型
class SRN(nn.Module):
    def __init__(self, input_size, hidden_size, W_attr=None, U_attr=None, b_attr=None):
        super(SRN, self).__init__()
        # 嵌入向量的维度
        self.input_size = input_size
        # 隐状态的维度
        self.hidden_size = hidden_size
        # 定义模型参数W，其shape为 input_size x hidden_size
        if W_attr == None:
            W = torch.zeros(size=[input_size, hidden_size], dtype=torch.float32)
        else:
            W = torch.tensor(W_attr, dtype=torch.float32)
        self.W = torch.nn.Parameter(W)
        # 定义模型参数U，其shape为hidden_size x hidden_size
        if U_attr == None:
            U = torch.zeros(size=[hidden_size, hidden_size], dtype=torch.float32)
        else:
            U = torch.tensor(U_attr, dtype=torch.float32)
        self.U = torch.nn.Parameter(U)
        # 定义模型参数b，其shape为 1 x hidden_size
        if b_attr == None:
            b = torch.zeros(size=[1, hidden_size], dtype=torch.float32)
        else:
            b = torch.tensor(b_attr, dtype=torch.float32)
        self.b = torch.nn.Parameter(b)

    # 初始化向量
    def init_state(self, batch_size):
        hidden_state = torch.zeros(size=[batch_size, self.hidden_size], dtype=torch.float32)
        return hidden_state

    # 定义前向计算
    def forward(self, inputs, hidden_state=None):
        # inputs: 输入数据, 其shape为batch_size x seq_len x input_size
        batch_size, seq_len, input_size = inputs.shape

        # 初始化起始状态的隐向量, 其shape为 batch_size x hidden_size
        if hidden_state is None:
            hidden_state = self.init_state(batch_size)

        # 循环执行RNN计算
        for step in range(seq_len):
            # 获取当前时刻的输入数据step_input, 其shape为 batch_size x input_size
            step_input = inputs[:, step, :]
            # 获取当前时刻的隐状态向量hidden_state, 其shape为 batch_size x hidden_size
            hidden_state = hidden_state + F.tanh(
                torch.matmul(step_input, self.W) + torch.matmul(hidden_state, self.U) + self.b)
        return hidden_state


# 基于RNN实现数字预测的模型
class Model_RNN4SeqClass(nn.Module):
    def __init__(self, model, num_digits, input_size, hidden_size, num_classes):
        super(Model_RNN4SeqClass, self).__init__()
        # 传入实例化的RNN层，例如SRN
        self.rnn_model = model
        # 词典大小
        self.num_digits = num_digits
        # 嵌入向量的维度
        self.input_size = input_size
        # 定义Embedding层
        self.embedding = Embedding(num_digits, input_size)
        # 定义线性层
        self.linear = nn.Linear(hidden_size, num_classes)

    def forward(self, inputs):
        # 将数字序列映射为相应向量
        inputs_emb = self.embedding(inputs)
        # 调用RNN模型
        hidden_state = self.rnn_model(inputs_emb)
        # 使用最后一个时刻的状态进行数字预测
        logits = self.linear(hidden_state)
        return logits


np.random.seed(0)
random.seed(0)
torch.manual_seed(0)

# 训练轮次
num_epochs = 50
# 学习率
lr = 0.2
# 输入数字的类别数
num_digits = 10
# 将数字映射为向量的维度
input_size = 32
# 隐状态向量的维度
hidden_size = 32
# 预测数字的类别数
num_classes = 19
# 批大小
batch_size = 64
# 模型保存目录
save_dir = "./checkpoints"

# 可以设置不同的length进行不同长度数据的预测实验
length = 20
print(f"\n====> Training SRN with data of length {length}.")

# 加载长度为length的数据
data_path = f"./datasets/{length}"
train_examples, dev_examples, test_examples = load_data(data_path)
train_set, dev_set, test_set = DigitSumDataset(train_examples), DigitSumDataset(dev_examples), DigitSumDataset(
    test_examples)
train_loader = torch.utils.data.DataLoader(train_set, batch_size=batch_size)
dev_loader = torch.utils.data.DataLoader(dev_set, batch_size=batch_size)
test_loader = torch.utils.data.DataLoader(test_set, batch_size=batch_size)
# 实例化模型
base_model = SRN(input_size, hidden_size)
model = Model_RNN4SeqClass(base_model, num_digits, input_size, hidden_size, num_classes)
# 指定优化器
optimizer = torch.optim.SGD(lr=lr, params=model.parameters())
# 定义评价指标
metric = Accuracy()
# 定义损失函数
loss_fn = nn.CrossEntropyLoss(reduction="sum")

# 基于以上组件，实例化Runner
runner = RunnerV3(model, optimizer, loss_fn, metric)

# 进行模型训练
model_save_path = os.path.join(save_dir, f"srn_explosion_model_{length}.pdparams")
runner.train(train_loader, dev_loader, num_epochs=num_epochs, eval_steps=100, log_steps=1,
             save_path=model_save_path, custom_print_log=custom_print_log)

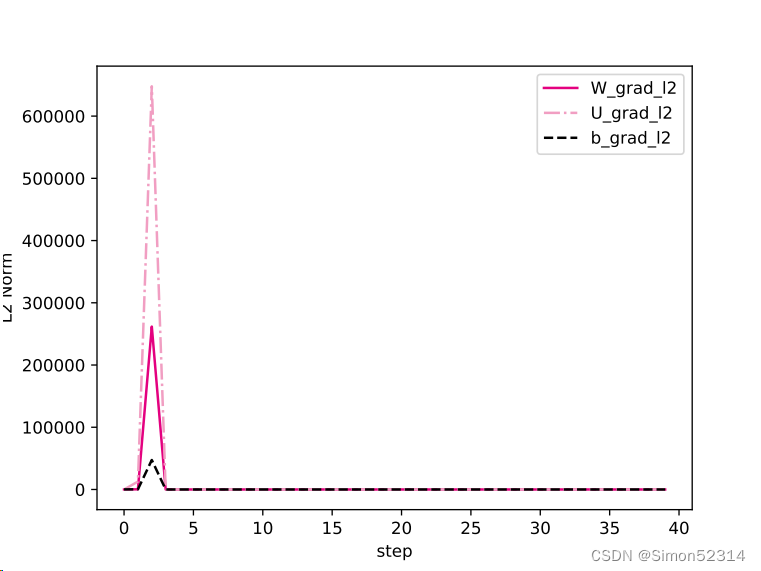
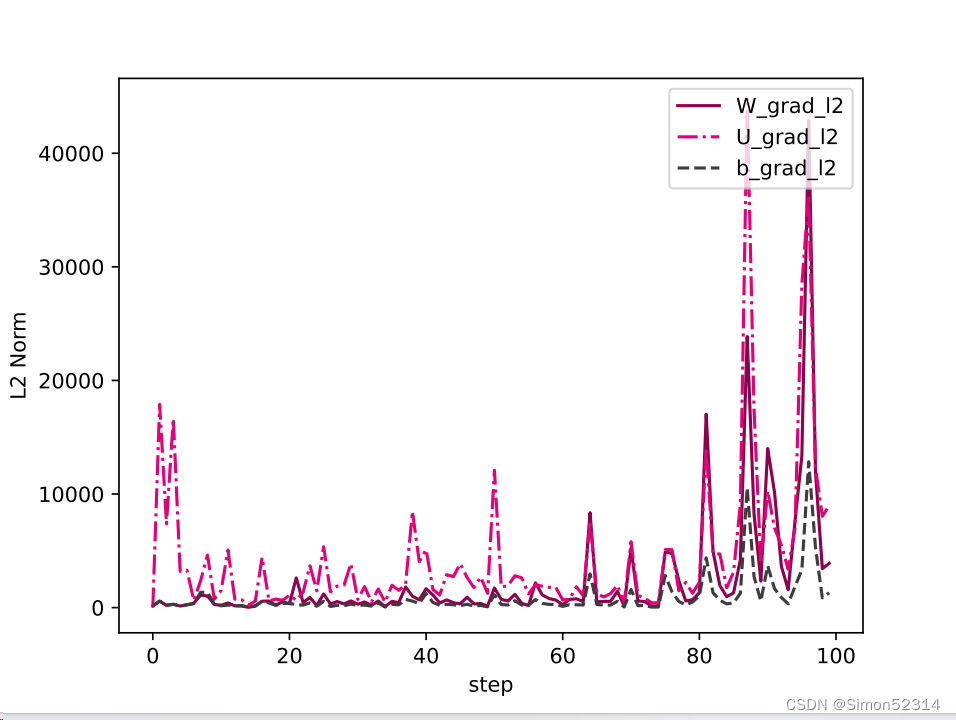
接下来，可以获取训练过程中关于W，U和b参数梯度的L2范数，并将其绘制为图片以便展示，相应代码如下：?

def plot_grad(W_list, U_list, b_list, save_path, keep_steps=40):
    # 开始绘制图片
    plt.figure()
    # 默认保留前40步的结果
    steps = list(range(keep_steps))
    plt.plot(steps, W_list[:keep_steps], "r-", color="#e4007f", label="W_grad_l2")
    plt.plot(steps, U_list[:keep_steps], "-.", color="#f19ec2", label="U_grad_l2")
    plt.plot(steps, b_list[:keep_steps], "--", color="#000000", label="b_grad_l2")
    plt.xlabel("step")
    plt.ylabel("L2 Norm")
    plt.legend(loc="upper right")
    plt.savefig(save_path)
    print("image has been saved to: ", save_path)
save_path = f"./images/6.8.pdf"
plot_grad(W_list, U_list, b_list, save_path)

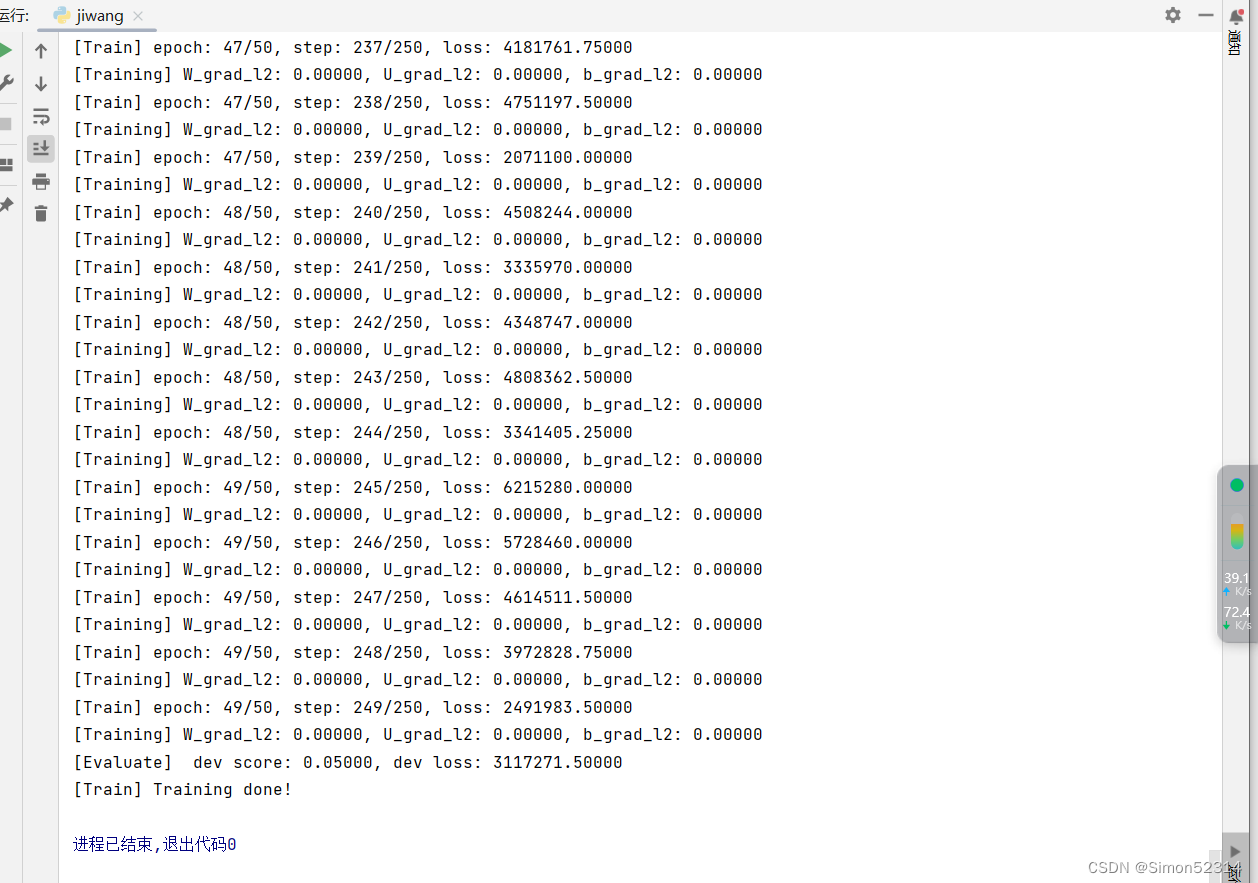
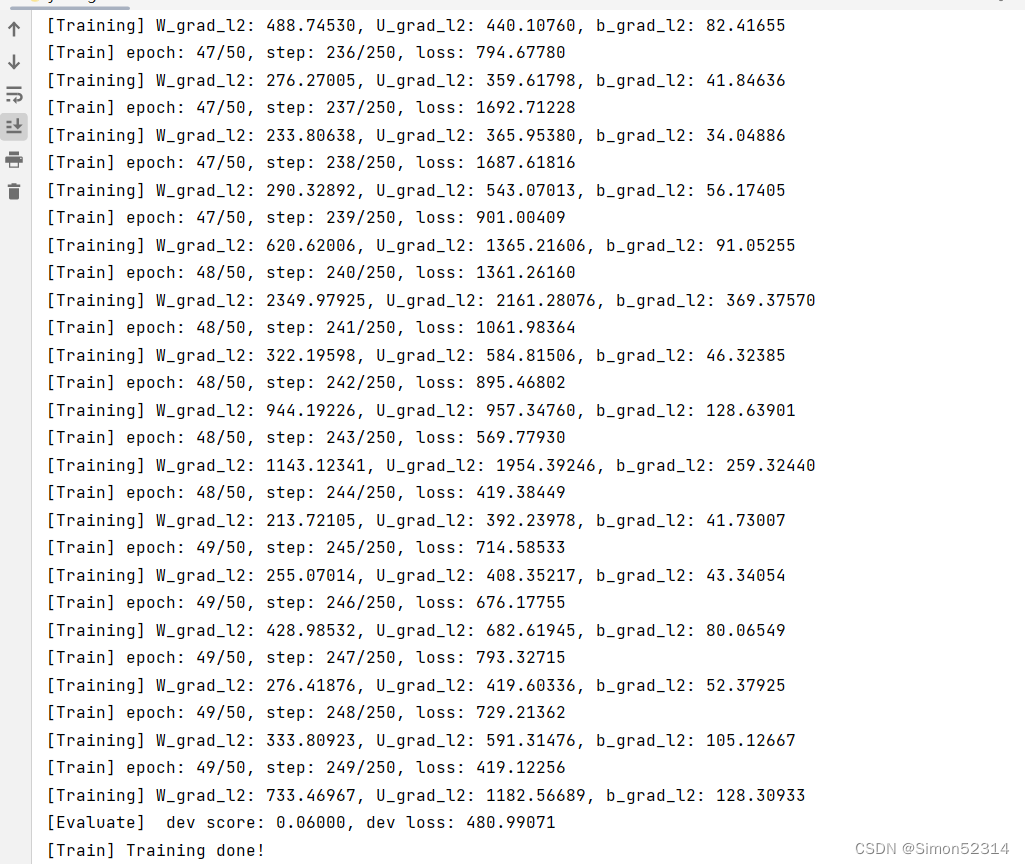
可以看到经过学习率等方式的调整，梯度范数急剧变大，而后梯度范数几乎为0. 这是因为TanhTanh为SigmoidSigmoid型函数，其饱和区的导数接近于0，由于梯度的急剧变化，参数数值变的较大或较小，容易落入梯度饱和区，导致梯度为0，模型很难继续训练.?

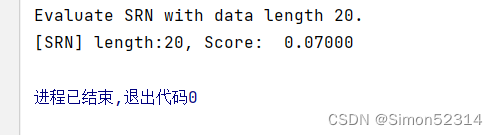
接下来，使用该模型在测试集上进行测试。

print(f"Evaluate SRN with data length {length}.")
# 加载训练过程中效果最好的模型
model_path = os.path.join(save_dir, f"srn_explosion_model_{length}.pdparams")
runner.load_model(model_path)

# 使用测试集评价模型，获取测试集上的预测准确率
score, _ = runner.evaluate(test_loader)
print(f"[SRN] length:{length}, Score: {score: .5f}")

6.2.3 使用梯度截断解决梯度爆炸问题?

梯度截断是一种可以有效解决梯度爆炸问题的启发式方法，当梯度的模大于一定阈值时，就将它截断成为一个较小的数。一般有两种截断方式：按值截断和按模截断．本实验使用按模截断的方式解决梯度爆炸问题。

按模截断是按照梯度向量g的模进行截断，保证梯度向量的模值不大于阈值b，裁剪后的梯度为:

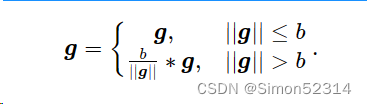
当梯度向量g的模不大于阈值b时，g数值不变，否则对g进行数值缩放。

在引入梯度截断之后，将重新观察模型的训练情况。这里我们重新实例化一下：模型和优化器，然后组装runner，进行训练。代码实现如下：

修改一下RunnerV3

class RunnerV3(object):
    def __init__(self, model, optimizer, loss_fn, metric, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric  # 只用于计算评价指标

        # 记录训练过程中的评价指标变化情况
        self.dev_scores = []

        # 记录训练过程中的损失函数变化情况
        self.train_epoch_losses = []  # 一个epoch记录一次loss
        self.train_step_losses = []  # 一个step记录一次loss
        self.dev_losses = []

        # 记录全局最优指标
        self.best_score = 0

    def train(self, train_loader, dev_loader=None, **kwargs):
        # 将模型切换为训练模式
        self.model.train()

        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_steps = kwargs.get("log_steps", 100)
        # 评价频率
        eval_steps = kwargs.get("eval_steps", 0)

        # 传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")

        custom_print_log = kwargs.get("custom_print_log", None)

        # 训练总的步数
        num_training_steps = num_epochs * len(train_loader)

        if eval_steps:
            if self.metric is None:
                raise RuntimeError('Error: Metric can not be None!')
            if dev_loader is None:
                raise RuntimeError('Error: dev_loader can not be None!')

        # 运行的step数目
        global_step = 0

        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            # 用于统计训练集的损失
            total_loss = 0
            for step, data in enumerate(train_loader):
                X, y = data
                # 获取模型预测
                logits = self.model(X)
                loss = self.loss_fn(logits, y.long())  # 默认求mean
                total_loss += loss

                # 训练过程中，每个step的loss进行保存
                self.train_step_losses.append((global_step, loss.item()))

                if log_steps and global_step % log_steps == 0:
                    print(
                        f"[Train] epoch: {epoch}/{num_epochs}, step: {global_step}/{num_training_steps}, loss: {loss.item():.5f}")

                # 梯度反向传播，计算每个参数的梯度值
                loss.backward()

                if custom_print_log:
                    custom_print_log(self)
                nn.utils.clip_grad_norm_(parameters=self.model.parameters(), max_norm=20, norm_type=2)
                # 小批量梯度下降进行参数更新
                self.optimizer.step()
                # 梯度归零
                self.optimizer.zero_grad()

                # 判断是否需要评价
                if eval_steps > 0 and global_step > 0 and \
                        (global_step % eval_steps == 0 or global_step == (num_training_steps - 1)):

                    dev_score, dev_loss = self.evaluate(dev_loader, global_step=global_step)
                    print(f"[Evaluate]  dev score: {dev_score:.5f}, dev loss: {dev_loss:.5f}")

                    # 将模型切换为训练模式
                    self.model.train()

                    # 如果当前指标为最优指标，保存该模型
                    if dev_score > self.best_score:
                        self.save_model(save_path)
                        print(
                            f"[Evaluate] best accuracy performence has been updated: {self.best_score:.5f} --> {dev_score:.5f}")
                        self.best_score = dev_score

                global_step += 1

            # 当前epoch 训练loss累计值
            trn_loss = (total_loss / len(train_loader)).item()
            # epoch粒度的训练loss保存
            self.train_epoch_losses.append(trn_loss)

        print("[Train] Training done!")

    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def evaluate(self, dev_loader, **kwargs):
        assert self.metric is not None

        # 将模型设置为评估模式
        self.model.eval()

        global_step = kwargs.get("global_step", -1)

        # 用于统计训练集的损失
        total_loss = 0

        # 重置评价
        self.metric.reset()

        # 遍历验证集每个批次
        for batch_id, data in enumerate(dev_loader):
            X, y = data

            # 计算模型输出
            logits = self.model(X)

            # 计算损失函数
            loss = self.loss_fn(logits, y.long()).item()
            # 累积损失
            total_loss += loss

            # 累积评价
            self.metric.update(logits, y)

        dev_loss = (total_loss / len(dev_loader))
        dev_score = self.metric.accumulate()

        # 记录验证集loss
        if global_step != -1:
            self.dev_losses.append((global_step, dev_loss))
            self.dev_scores.append(dev_score)

        return dev_score, dev_loss

    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def predict(self, x, **kwargs):
        # 将模型设置为评估模式
        self.model.eval()
        # 运行模型前向计算，得到预测值
        logits = self.model(x)
        return logits

    def save_model(self, save_path):
        torch.save(self.model.state_dict(), save_path)

    def load_model(self, model_path):
        state_dict = torch.load(model_path)
        self.model.load_state_dict(state_dict)

实例化模型：

# 清空梯度列表
W_list.clear()
U_list.clear()
b_list.clear()
# 实例化模型
base_model = SRN(input_size, hidden_size)
model = Model_RNN4SeqClass(base_model, num_digits, input_size, hidden_size, num_classes)
 
# 定义clip，并实例化优化器
 
optimizer = torch.optim.SGD(lr=lr, params=model.parameters())
# 定义评价指标
metric = Accuracy()
# 定义损失函数
loss_fn = nn.CrossEntropyLoss(reduction="sum")
 
# 实例化Runner
runner = RunnerV3(model, optimizer, loss_fn, metric)
 
# 训练模型
model_save_path = os.path.join(save_dir, f"srn_fix_explosion_model_{length}.pdparams")
runner.train(train_loader, dev_loader, num_epochs=num_epochs, eval_steps=100, log_steps=1, save_path=model_save_path, custom_print_log=custom_print_

图像化：

save_path =  f"./images/6.9.pdf"
plot_grad(W_list, U_list, b_list, save_path, keep_steps=100)

可以看到，随着迭代步骤的进行，梯度始终保持在一个有值的状态，表明按模截断能够很好地解决梯度爆炸的问题.?

接下来，使用梯度截断策略的模型在测试集上进行测试。

print(f"Evaluate SRN with data length {length}.")

# 加载训练过程中效果最好的模型
model_path = os.path.join(save_dir, f"srn_fix_explosion_model_{length}.pdparams")
runner.load_model(model_path)

# 使用测试集评价模型，获取测试集上的预测准确率
score, _ = runner.evaluate(test_loader)
print(f"[SRN] length:{length}, Score: {score: .5f}")

? ? ?由于为复现梯度爆炸现象，改变了学习率，优化器等，因此准确率相对比较低。但由于采用梯度截断策略后，在后续训练过程中，模型参数能够被更新优化，因此准确率有一定的提升。?

总结：

1、

这是在飞浆中用的函数，那么在torch 中可以使用什么呢？

pytorch中应该使用torch.nn.utils.clip_grad_value_(model.parameters(), value)这个函数

2、 了解了范数的概念，以及范数可以反应梯度的大小，打印范数可以及时了解梯度的大小

3、这次了解了梯度截断的两种情况

梯度截断的原因：

由于进行反向传播时，进行每一层的梯度计算，假设梯度都是比较大的值，计算到第一层的梯度时，会呈指数级增长，那么更新完的参数值也会很大，越来越大，就会产生梯度爆炸的现象，找不到最优解。

方法：

?

?

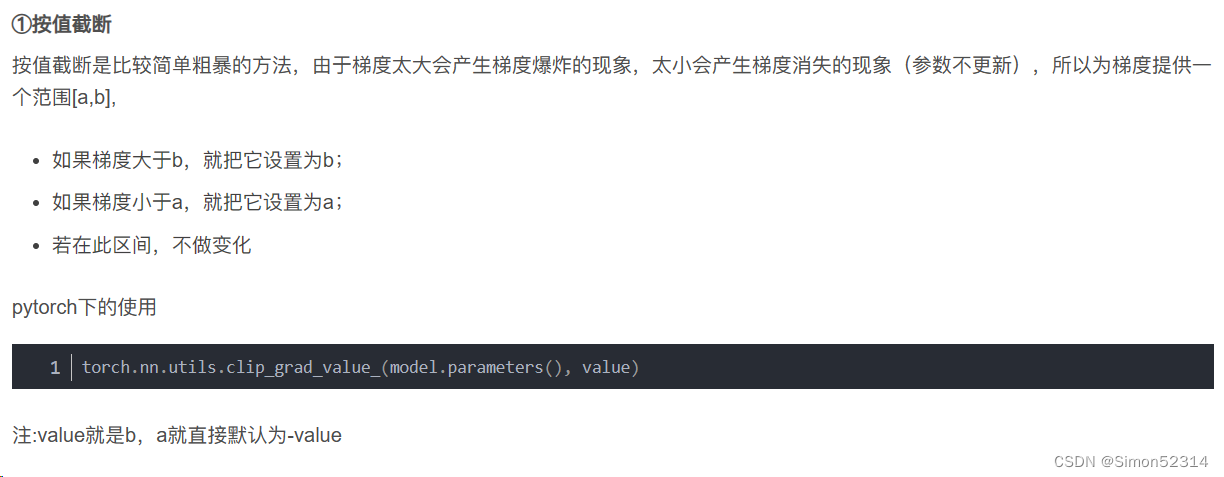参考链接：?

神经网络优化（1）之梯度截断-CSDN博客

范数（简单的理解）、范数的用途、什么是范数_矩阵范数的意义-CSDN博客

?

?