代码随想录算法训练营第二十天| 回溯 理论基础 77. 组合

理论基础

回溯是一种搜索的方式。回溯是递归的副产品，只要有递归就会有回溯，回溯函数也是递归函数，指的是一个函数。

回溯法并不是什么高效的算法。因为回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。

回溯法解决的问题

• 组合问题：N个数里面按一定规则找出k个数的集合（不强调元素顺序）
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 排列问题：N个数按一定规则全排列，有几种排列方式（强调元素顺序）
• 棋盘问题：N皇后，解数独等等

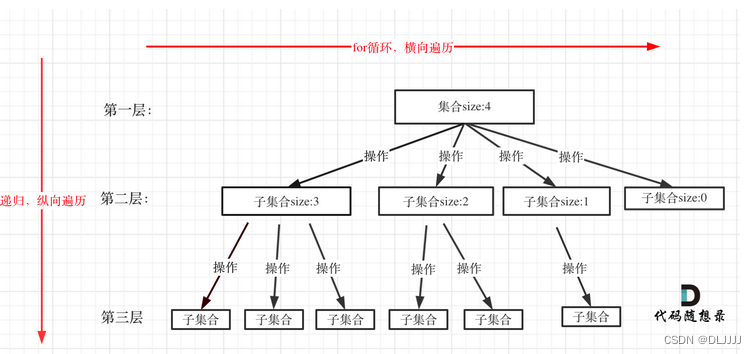
回溯法解决的问题都可以抽象为树形结构，因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

回溯法模板

回溯函数模板返回值以及参数：回溯算法中函数返回值一般为void。因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来，所以一般是先写逻辑，然后需要什么参数，就填什么参数。

回溯函数终止条件：一般来说搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。

回溯搜索的遍历过程：回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成的树的深度。

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

77. 组合

可以将题目看成一个n叉树的结构

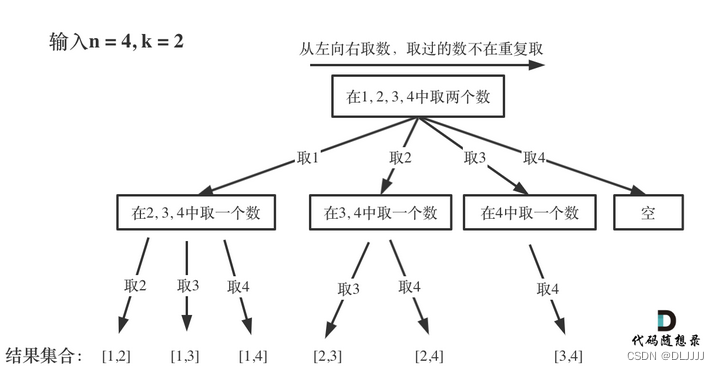
当到达叶子结点的时候，例如图中[1,2]的时候，需要返回，此时为了能够取到[1,3]，需要进行回溯的操作，将存放[1,2]的容器弹出一个，完成回溯。

递归函数的返回值以及参数：一般为void类型

递归函数终止条件：path这个数组的大小如果达到k，说明我们找到了一个子集大小为k的组合了

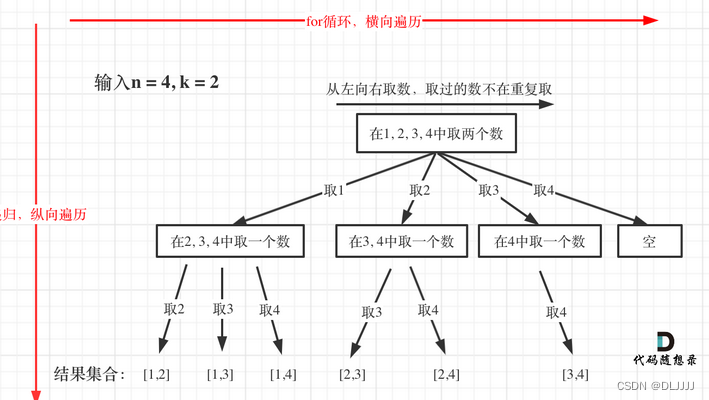
递归函数单层逻辑：回溯法的搜索过程就是一个树型结构的遍历过程，在如下图中，可以看出for循环用来横向遍历，递归的过程是纵向遍历。

class Solution {
public:
    vector<vector<int>> res;
    void backtracing(vector<int> path,int k,int index,int n){
        if(path.size()==k){
            res.push_back(path);
            return  ; 
        }
        for(int i=index;i<=n;i++ ){
            path.push_back(i);
            backtracing(path,k,i+1,n);
            path.pop_back();
        }

    }

    vector<vector<int>> combine(int n, int k) {
        int index=1;
        vector<int> path;
        backtracing(path,k,index,n);
        return res;
    }
};  

77.组合（剪枝）

n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。因此可以在for循环那边做文章，在第一层便可以设置第一层可以取什么数字，第二层设置第二层该取的数字。

1. 已经选择的元素个数：path.size();

2. 所需需要的元素个数为: k - path.size();

3. 列表中剩余元素（n-i） >= 所需需要的元素个数（k - path.size()）

4. 在集合n中至多要从该起始位置 : i <= n - (k - path.size()) + 1，开始遍历

第4点加1表示此时需要取到起始位置，以n=4，k=4为例，不加1表示i<=0，根本进不了for循环。

只需将for循环修改

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置

?完整代码：

class Solution {
public:
    vector<vector<int>> res;
    void backtracing(vector<int> path,int k,int index,int n){
        if(path.size()==k){
            res.push_back(path);
            return  ; 
        }
        for(int i=index; i <= n - (k - path.size()) + 1;i++ ){
            path.push_back(i);
            backtracing(path,k,i+1,n);
            path.pop_back();
        }
    
    }

    vector<vector<int>> combine(int n, int k) {
        int index=1;
        vector<int> path;
        backtracing(path,k,index,n);
        return res;
    }
};