矩阵特征值解决微分方程问题【2】

目录

一. 特征值与特征向量介绍

1.1 介绍

1.2 小结

二. 特征值求解微分方程

2.1 常微分方程

2.2 其他应用

三. 总结

---

一. 特征值与特征向量介绍

本文章需要用到的基础理论：

1. 奇异矩阵的行列式为0

1.1 介绍

已知：

如果已知特征值，那么这就是一个线性方程。由此可得：

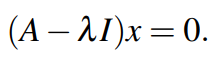
根据矩阵的子空间理论，向量x位于的零空间内。其中，需要保证的子空间有非零项。

综上可得矩阵必须是奇异矩阵，利用其行列式（determinant）可得：

这就是一个关于的特征方程，每一个对应的解，都有对应的向量x。

利用矩阵特征值解决微分方程【1】-CSDN博客

承接上文，可得新的矩阵：

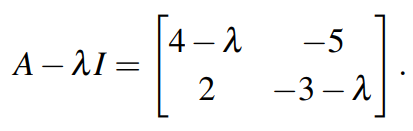
计算该矩阵的行列式：

以上也被称之为特征多项式。该多项式的根即为特征值。利用求根公式或者十字相乘法，易得解为：

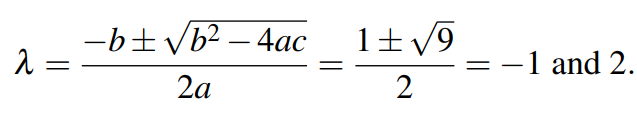
对于2行2列的矩阵，其特征方程是二次的，特征值也应该有两个。奇异矩阵的行列式为0，并且奇异矩阵的零空间存在非零项。根据经验，特征向量通常不知一个，由此也可以形成子空间。

比如当特征值求出为-1时，可求其特征向量如下：

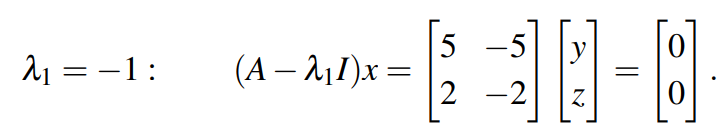
很明显第一个特征向量如下：（成倍数也可以）

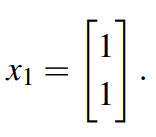
对于第二个特征向量的计算也类似，可得：

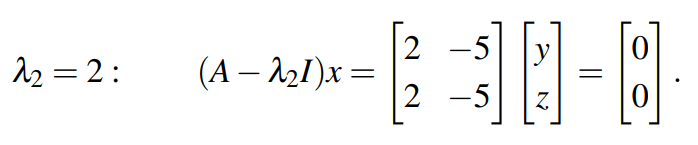
由此解出特征向量为：

一个很有意思的现象：

1. 的列是第二个特征向量；
2. 的列是第一个特征向量；

所有的特征向量都在矩阵的零空间中，也被称之为特征空间（eigenspace）。在本例中，第一个特征空间是经过的一条线，第二个特征空间是经过的一条线。

1.2 小结

对任意矩阵A求解特征值与特征向量总共分成三步：

第一步：

计算的特征值，其中只会出现在对角线处。该特征值是一个次数为n的多项式，其第一项一定是

第二步：

求多项式的根。一共有n个根，全是矩阵A的特征值；

第三步：

对于每个特征值，计算如下方程：

因为矩阵的行列式为0，所以该方程存在非零解。这些非零解就是特征向量。

二. 特征值求解微分方程

2.1 常微分方程

承接上文（前面已经给出了一个链接），函数u满足：

该方程的其中一个特殊解为：

以上我们求出了两个特征值和两个特征向量，所以可得：

对这两个结果进行和倍组合，结果也符合条件，由此进行相加（superposition），可得：

从线性代数的角度来讲就是，零空间一定属于矩阵的子空间，所以对结果进行线性组合依旧在此空间上。

以上和又被称之为自由变量（free parameter）。这两个参数的值取决于初始条件，也就是：

根据上一篇文章（链接在上面），可得初始条件为：

其中第一个矩阵为特征向量形成的矩阵。8和5为初始的条件，和是我们需要求的自由变量。二维方程还是很好解的，易得该方程的两个解为3和1

由此原始的方程为：

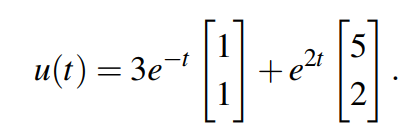
函数u是由v和w组合而成的，又根据v(0)=8，w(0)-=5，可得最终的结果为：

至此我们利用矩阵的特征值和特征向量x解决了二维的微分方程。

2.2 其他应用

除此以外，在网络安全中信道矩阵的特征值也是一个很重要的参数。还有：

桥的频率（特征值）与行人步伐的频率；

火箭的频率与燃料晃动（sloshing of fuel）频率，风的频率等。

这些其实都跟矩阵的特征值相关。

三. 总结

矩阵的概念产生于十九世纪中叶，是为了线性方程组的需要而产生的。“矩阵 Matrix”的术语是由西尔维斯特首次提出的，之后，由凯莱明确其概念，创立了矩阵理论，系统而全面地阐述了矩阵的理论体系，后来，由弗洛伯纽斯等人继续发展和完善矩阵理论体系，进而形成了现代矩阵理论。

而中国早在公元前一世纪的《九章算术》中就已经开始使用类似矩阵的名词，遗憾的是那时矩阵只是用于解决一些实际问题，并没有系统地提出矩阵理论。

矩阵理论中的特征值与特征向量问题是矩阵理论的重要组成部分之一，与此同时它又贯穿于常微分方程、高等代数等学科。矩阵的特征值与特征向量问题不仅可以解决数学中相关的计算问题，在物理、生物、网络安全领域中也发挥着重要的作用。伴随着科技的快速发展，社会发展的速度与日俱增，代数作为数学中的一门基础科目已经渗透于众多领域，它在其他领域的地位越来越重要。在代数问题的研究过程中，大量的问题转化为矩阵问题。也就使矩阵成为代数特别是线性代数的一个主要研究对象。
特征值与特征向量是线性代数研究的主要问题之一，两者密切相关，在数学与实际生活中应用广泛。矩阵的特征值与特征向量在常微分方程、层次分析以及保护环境中都有应用。　

（1）特征值与特征向量在常微分方程中的应用

特征值与特征向量在数学中应用广泛，尤其是在常微分方程中对于常系数线性微分方程组的解法中起着十分重要的作用，对于齐次线性方程组的通解问题，就是求其基本解组。

（2）特征值特征向量确定权重大小的方法

通过运用特征值特征向量相关知识计算出权重的大小，进一步计算出加权平均给出最佳的决策。

（3）特征值与特征向量在保护环境中的应用

特征值与特征向量在保护环境中的应用：解决这类问题的关键是要把实际问题转化为数学语言，特别是矩阵语言，然后再利用特征值与特征向量来解决问题，利用列矩阵转换矩阵的乘法运算，实现由当前状态来预测下一阶段的不同状态，这是矩阵的一个重要应用，从这里我们可以进一步体会矩阵在社会经济领域里的价值 。
?