仿真机器人-深度学习CV和激光雷达感知(项目2)day6【数学基础-坐标变换】

发布时间：2024年01月24日

文章目录

前言
坐标变换的作用
旋转与平移
齐次坐标
变换矩阵
旋转的其他表示方法*

前言

💫你好，我是辰chen，本文旨在准备考研复试或就业
💫本文内容是我为复试准备的第二个项目
💫欢迎大家的关注，我的博客主要关注于考研408以及AIoT的内容
🌟 预置知识：基本Python语法，基本linux命令行使用

以下的几个专栏是本人比较满意的专栏(大部分专栏仍在持续更新)，欢迎大家的关注：

💥ACM-ICPC算法汇总【基础篇】
💥ACM-ICPC算法汇总【提高篇】
💥AIoT(人工智能+物联网)
💥考研
💥CSP认证考试历年题解

坐标变换的作用

把坐标在坐标系之间转换(把变换应用到一个坐标)

世界中有多个物体，想获取物体间的相对位置.
自动驾驶中，拿到了自车和附近其他车辆的坐标(世界坐标系)，需要计算附近车辆与自车的相对位置，即把车辆坐标从世界坐标系转换到自车坐标系
机器人有多个组成部分，想获取各个部分的位置.
机械臂有多个关节，每个关节都对应一个坐标系，需要计算机械臂末端(机械手)相对于机械臂本体的位置，即把机械手坐标从自身坐标系转换到本体坐标系
定位节点发布地图到里程计的变换，里程计节点发布里程计到机器人的变换，需要计算机器人在地图中的位置，即把机器人坐标从里程计坐标系转换到地图坐标系

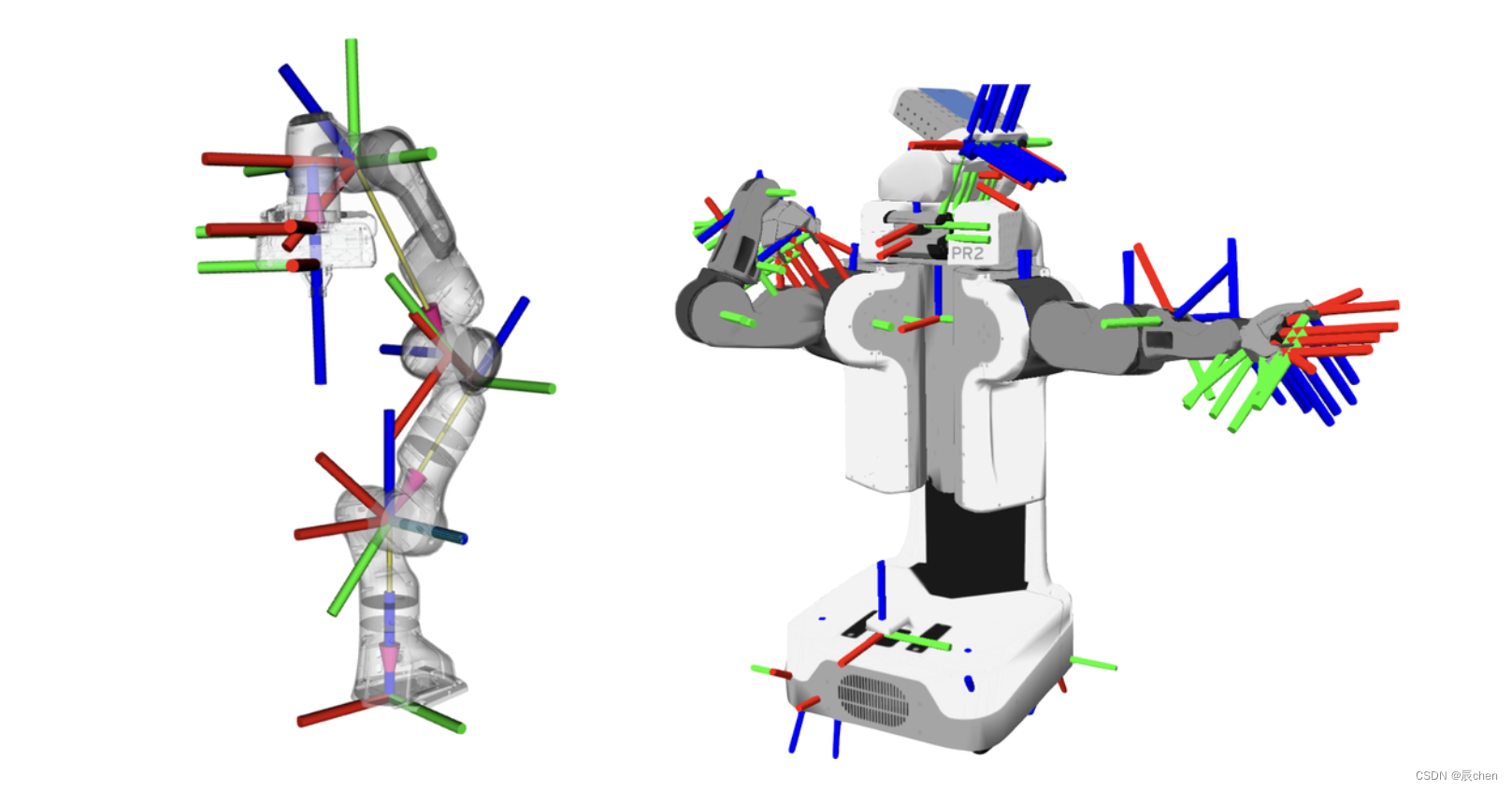
在这里插入图片描述

旋转与平移

二维变换

旋转

在这里插入图片描述
$x'=xcos\theta-ysin\theta$
$y'=xsin\theta+ycos\theta$

将上述表达式写成矩阵乘积的形式：

$\left[ \begin{matrix} x' \\ y' \\ \end{matrix} \right] = \left[ \begin{matrix} cos\theta & -sin\theta \\ sin\theta &cos\theta \\ \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ \end{matrix} \right]$

上图中，点逆时针旋转 $\theta$ ，等价于坐标系顺时针旋转 $\theta$ ，假设原坐标系为 A，坐标系顺时针旋转 $\theta$ 后得到坐标系 B

定义符号：

$P_m^A:$ 点 $m$ 在坐标系 $A$ 下的坐标
$R_A^B:$ 坐标系 $A$ 到 $B$ 的旋转矩阵

只考虑旋转，则有 $P_m^B=R_A^B×P_m^A$

平移

$\left[ \begin{matrix} x' \\ y' \\ \end{matrix} \right] = \left[ \begin{matrix} x \\ y \\ \end{matrix} \right] + \left[ \begin{matrix} t_x \\ t_y \\ \end{matrix} \right]$
定义符号：

$P_{Aorg}^B:$ 坐标系 A 的原点在坐标系 B 中的位置

只考虑平移，则有 $P_m^B=P_m^A+P_{Aorg}^B$

推广到三维

$\begin{bmatrix} x_A \\ y_A \\ z_A \end{bmatrix}= \begin{bmatrix} \cos \langle i_B, i_A \rangle & \cos \langle j_B, i_A \rangle & \cos \langle k_B, i_A \rangle \\ \cos \langle i_B, j_A \rangle & \cos \langle j_B, j_A \rangle & \cos \langle k_B, j_A \rangle \\ \cos \langle i_B, k_A \rangle & \cos \langle j_B, k_A \rangle & \cos \langle k_B, k_A \rangle \end{bmatrix} \begin{bmatrix} x_B \\ y_B \\ z_B \end{bmatrix} = R \begin{bmatrix} x_B \\ y_B \\ z_B \end{bmatrix}$

推导过程无需掌握，推导过程可见博客：3. 机器人正运动学—坐标系及其变换

平移矩阵与二维类似。

齐次坐标

问题引入

一个完整的变换包括平移和旋转： $P_m^B=R_A^B×P_m^A+P_{Aorg}^B$

但这种描述不够紧凑，面对多重连续变换时，会变得很臃肿：
$P_m^C=R_B^C×(R_A^B×P_m^A+P_{Aorg}^B)+P_{Borg}^C$

Q：有没有方法仅使用一次矩阵乘法，就同时完成平移和旋转？
A：有，使用齐次坐标

定义

用 n+1 维向量来表示 n 维空间的点
$\left[ \begin{matrix} x \\ y \\ \end{matrix} \right] \rightarrow \left[ \begin{matrix} x \\ y \\ 1 \\ \end{matrix} \right]$
在原有旋转矩阵的基础上扩展一维用于容纳平移关系

用法

$\begin{bmatrix} a' \\ 1 \end{bmatrix}= \begin{bmatrix} R & t \\ 0^T & 1 \end{bmatrix} \begin{bmatrix} a \\ 1 \end{bmatrix} \triangleq T \begin{bmatrix} a \\ 1 \end{bmatrix}$

$\begin{bmatrix} P^A_M \\ 1 \end{bmatrix}= T_B^{A} \cdot \begin{bmatrix} P^B_M \\ 1 \end{bmatrix}$

$T_B^{A} = \begin{bmatrix} R_B^A & P_{Borg}^A \\ 0 & 1 \end{bmatrix}$

变换矩阵

定义符号

$T_A^B:$ 坐标系 A 到 B 的变换矩阵

使用变换矩阵同时进行旋转和平移
$P_m^B=T_A^B×P_m^A$

可以连续变换：
$P_m^C=T_B^C×T_A^B×P_m^A$

参考视频辅助理解（视频中的缩放矩阵用不到，无需理解）：无所不能的矩阵 - 三维图形变换

旋转的其他表示方法*

* 扩展内容，了解其存在和作用即可

旋转矩阵
- 优点：可以直接进行矩阵运算
- 缺点：元素多，占用空间大（n 维空间需要 n * n 个元素）
欧拉角
- [Roll, Pitch, Yaw]
- 优点：直观，方便人类理解
- 缺点：万向节死锁，即在某些角度下丢失一个方向上的旋转能力（这个不重要，了解即可），详细可参考视频：无伤理解欧拉角中的“万向死锁”现象

在这里插入图片描述

四元数
- [x, y, z, w]
- 优点：能表示所有选抓（没有万向节死锁）
- 缺点：不能直观读懂

旋转矩阵、欧拉角、四元数之间可以进行转换，转换过程涉及到大量数学细节，不需要掌握。编程中，有现成的数学库实现了转换功能，直接使用即可。

上述所有内容出处如下，博主在此基础上仅为添加个人理解：
本项目为北大团队出品【项目三：深度学习&仿真机器人 - 丘丘老师】原创（部分代码为开源代码）。课程团队：B站ID【M学长的考研top帮】UID【3546580235848566】复试项目班QQ大群：885884619，负责人QQ：674799

文章来源:https://blog.csdn.net/qq_52156445/article/details/135778924
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！