最小二乘法解线性回归

最小二乘法

算法介绍

基于均方误差最小化来进行模型求解的方法称为“最小二乘法(least square method)它的主要思想就是选择未知参数，(a5，b5)(a3，b3)(a1，b1)(a4，b4)(a2，b2)使得理论值与观测值之差的平方和达到最小。

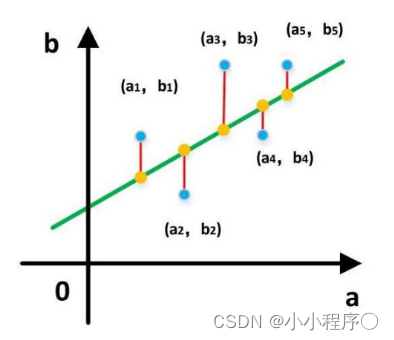
我们假设输入属性 (特征) 的数目只有一个

在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧式距离之和最小。

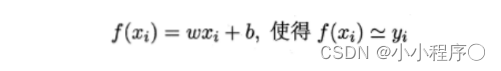
最小二乘法求解线性回归

求解w和b，使得 E(w)=(y - zi-)最小化的过程，称为线性回归模型的“最小二乘参数估计
将 E(w,6) 分别对w和b求导，可以得到

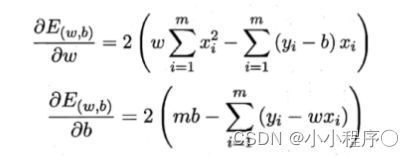
令偏导数都为0，可以得到

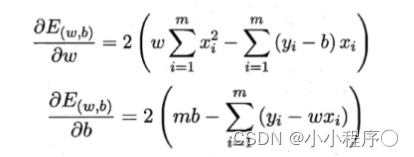
梯度下降法和最小二乘法

相同点
本质和目标相同:两种方法都是经典的学习算法，在给定已知数据的前提下利用求导算出一个模型(函数)，使得损失函数最小，然后对给定的新数据进行估算预测
不同点
损失函数:梯度下降可以选取其它损失函数，而最小二乘一定是平方损失函数实现方法:最小二乘法是直接求导找出全局最小;而梯度下降是一种迭代法效果:最小二乘找到的一定是全局最小，但计算繁琐，且复杂情况下未必有解;梯度下降迭代计算简单，但找到的一般是局部最小，只有在目标函数是凸函数时才是全局最小:到最小点附近时收敛速度会变慢，且对初始点的选择极为敏感