代码随想录算法训练营Day04|24. 两两交换链表中的结点、19.删除链表的倒数第N个结点、面试题 02.07. 链表相交、142.环形链表II

---

24. 两两交换链表中的结点

题目描述： 给定一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

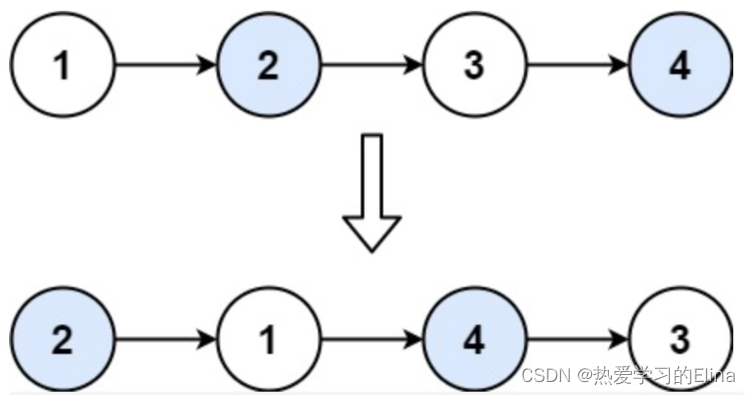
1.递归法

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode swapPairs(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode newHead = head.next;
        head.next = swapPairs(newHead.next);
        newHead.next = head;
        return newHead;
    }
}

2.虚拟头结点法

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

class Solution {
    // 虚拟头节点
    public ListNode swapPairs(ListNode head) {
        ListNode dummyNode = new ListNode(0);
        dummyNode.next = head;
        ListNode prev = dummyNode;

        while (prev.next != null && prev.next.next != null) {
            ListNode temp = head.next.next; // 缓存next
            prev.next = head.next;  // 将 prev 的next 改为 head 的 next
            head.next.next = head;  // 将 head.next(prev.next) 的next，指向 head
            head.next = temp;  // 将head的next接上缓存的temp
            prev =head;  // 步进一位
            head = head.next;  // 步进一位
        }
        return dummyNode.next;
    }
}

19.删除链表的倒数第N个结点

题目描述： 给定一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

1.双指针法

• 时间复杂度：$O(L)$
• 空间复杂度：$O(1)$

（1） 定义快慢指针，初始值为虚拟头结点；

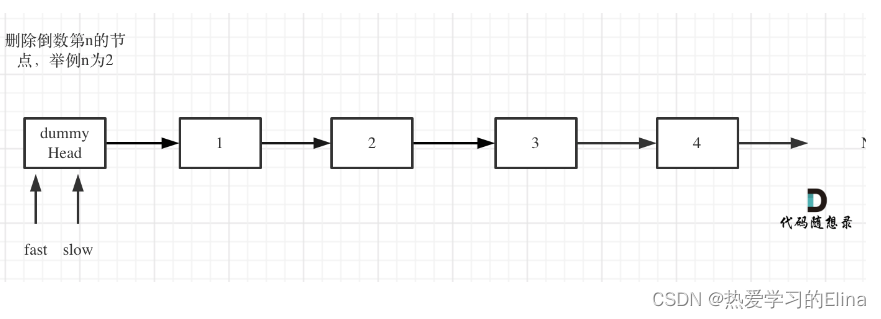（2）fast首先走n + 1步 ，为什么是n+1呢，因为只有这样同时移动的时候slow才能指向删除节点的上一个节点（方便做删除操作）；

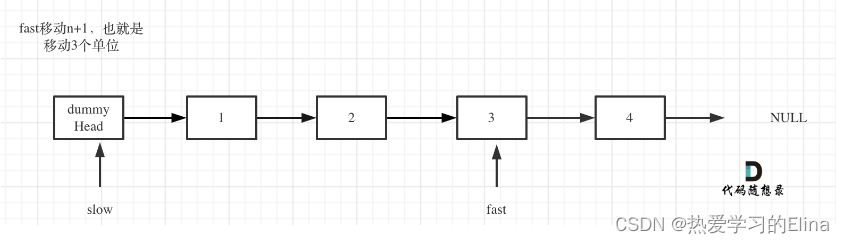
（3）fast和slow同时移动，直到fast指向末尾；

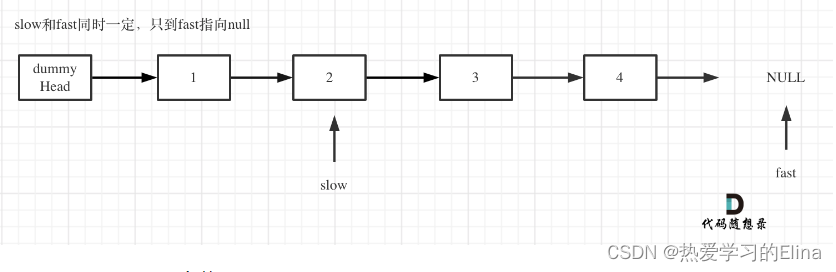
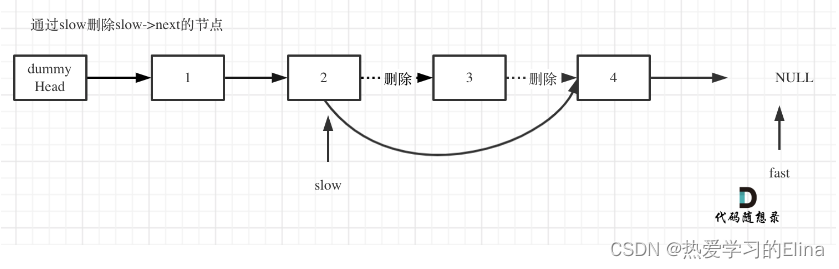
（4）删除slow指向的下一个结点。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummy = new ListNode(-1);
        dummy.next = head;
 
        ListNode slow = dummy;
        ListNode fast = dummy;
        while(n-- > 0) {
            fast = fast.next;
        }
        // 记住，待删除节点slow的上一结点
        ListNode prev = null;
        while (fast != null) {
            prev = slow;
            slow = slow.next;
            fast = fast.next;
        }
        // 上一结点next指针绕过 待删除节点slow 直接指向slow的下一结点
        prev.next = slow.next;
        // 释放 待删除结点slow 的next指针
        slow.next = null;
        return dummy.next;
    }
}

面试题 02.07. 链表相交

题目描述： 给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

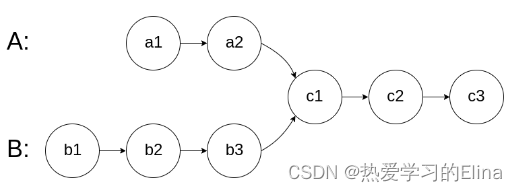
简单来说，就是求两个链表交点节点的指针。交点不是数值相等，而是指针相等。

• 时间复杂度：$O(n+m)$
• 空间复杂度：$O(1)$

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode curA = headA;
        ListNode curB = headB;
        int lenA = 0, lenB = 0;
        while (curA != null) {  // 求链表A的长度
            lenA ++;
            curA = curA.next;
        }
        while (curB != null) {  // 求链表B的长度
            lenB++;
            curB = curB.next;
        }
        curA = headA;
        curB = headB;
        // 让curA为最长链表的头，lenA为其长度
        if (lenB > lenA) {
            int tmpLen = lenA;
            lenA = lenB;
            lenB = tmpLen;

            ListNode tmpNode = curA;
            curA = curB;
            curB = tmpNode;
        }

        // 求长度差
        int gap = lenA - lenB;
        // 让curA和curB在同一起点上
        while (gap-- > 0) {
            curA = curA.next;
        }
        // 遍历curA和curB,遇到相同则直接返回
        while (curA != null) {
            if (curA == curB) {
                return curA;
            }
            curA = curA.next;
            curB = curB.next;
        }
        return null;
        
    }
}

---

142.环形链表II

题目描述： 给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

主要考察两知识点：

1. 判断链表是否环

• 双指针法判断是否有环，分别定义 fast 和 slow 指针，从头结点出发，fast指针每次移动两个节点，slow指针每次移动一个节点，如果 fast 和 slow指针在途中相遇 ，说明这个链表有环。（简单理解：两个人绕操场匀速跑圈，跑的快的人一定在某一时刻追上跑的慢的人）

2. 如果有环，如何找到这个环的入口
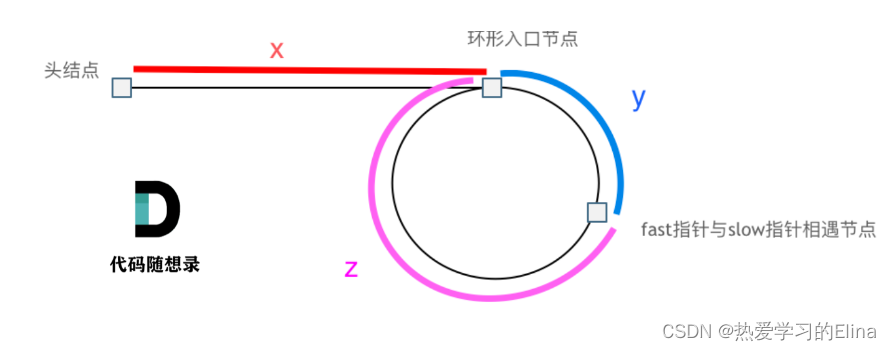
   （1）假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示：
   
   （2）那么相遇时： slow指针走过的节点数为: x+y，fast指针走过的节点数：x+y n (y+z)，n为fast指针在环内走了n圈才遇到slow指针,(y+z)为 一圈内节点的个数A。
   （3）整理公式之后：x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的，因为 fast指针至少要多走一圈才能相遇slow指针。

• 当n=1时：从头结点出发一个指针，从相遇节点 也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点。
• 当n＞1时：就是fast指针在环形转n圈之后才遇到 slow指针。其实这种情况和n=1的时候 效果是一样的，一样可以通过这个方法找到 环形的入口节点，只不过，index1 指针在环里 多转了(n-1)圈，然后再遇到index2，相遇点依然是环形的入口节点。

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
                ListNode index1 = fast;
                ListNode index2 = head;
                // 两个指针，从头结点和相遇结点，各走一步，直到相遇，相遇点即为环入口
                while (index1 != index2) {
                    index1 = index1.next;
                    index2 = index2.next;
                }
                return index1;
            }
        }
        return null;
        
    }
}

---

总结

以上就是今天学习的内容，双指针法是重点，不仅数组中可以用，链表中同样非常好用。环形链表中找环形入口较难，需要用数学思维分析和理解。