D34|不同路径

62.不同路径

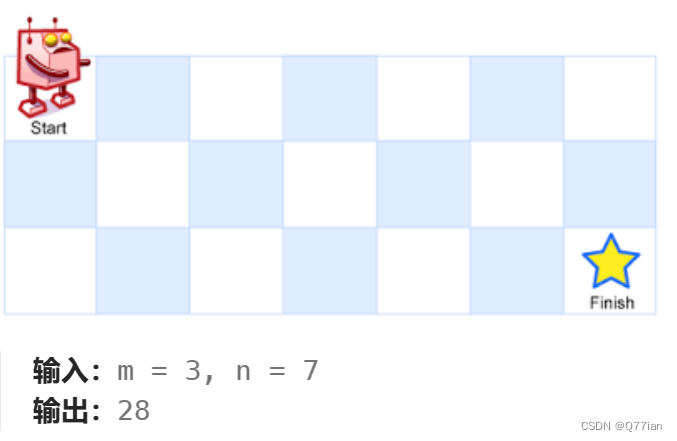
初始思路：

1）确定dp数组以及下标的含义：

? ? ? ? ? ? ? ?dp[i][i]存放到第i+1行和第i+1列的方法数

2）确定递推公式：

? ? ? ? dp[i][i]?= dp[i -1][i]?+ dp[i][i-1]

3）dp数组如何初始化

? ? ? ? 第0行是1；

? ? ? ? 第0列是1；

4）确定遍历顺序

从前到后

5）举例推导dp数组

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for(int i = 0;i<m;i++){
            dp[i][0] = 1;
        }
        for(int i = 0;i<n;i++){
            dp[0][i] = 1;
        }
        for(int i =1;i<m;i++){
            for(int j = 1;j<n;j++){
                dp[i][j] = dp[i][j-1] + dp[i-1][j];
            }
        }
        return dp[m-1][n-1];
    }
}

题解复盘：

? ? ? ? 基本一致?。

---

?63. 不同路径 II

初始思路：

在前一题的基础之上增加了对障碍数组的判断，如果第一行中有一个障碍，那么这个障碍后面的dp全部赋值为0，前面的都赋值为1；列同理。

再过程中遇到障碍，令当前dp为0即可。

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];
        for(int i = 0;i<m;i++){
           if(obstacleGrid[i][0]==1){
                break;
            }
            dp[i][0] = 1;

        }
        for(int i = 0;i<n;i++){
            if(obstacleGrid[0][i]==1){
                break;
            }
            dp[0][i] = 1;
        }
        for(int i =1;i<m;i++){
            for(int j = 1;j<n;j++){
                if(obstacleGrid[i][j]==1){dp[i][j] = 0;}
                else{
                    dp[i][j] = dp[i][j-1] + dp[i-1][j];
                }
            }
        }
        return dp[m-1][n-1];
    }
}

?