力扣精选算法100题——等于目标值的两个数or三数之和(双指针专题）

目录

🚩等于目标值的俩个数

第一步：了解题意

第二步：算法原理

第三步：代码实现

🚩三数之和

?第一步：了解题意

第二步：算法原理

思路：

?不漏：

?去重:

！优化

第三步：代码实现

🚩等于目标值的俩个数

?本题链接——等于目标值的俩个数?

第一步：了解题意

其实很好理解：我们在一个数组里面找到2个数等于target值即可，如果存在多种结果都等于target，只需要返回一组即可。

第二步：算法原理

?

就拿示例1来分析：

3和15符合题意，15和3也符合，只要返回一组即可。

我们怎么找到呢？遇到找到之和等于目标值一般都是用双指针来。

但是这个左右双指针并不是同向的，而是一个left定义在最初的位置，一个right定义在最右边的位置。如果left+right的值等于目标值，则就返回该值，如果小于目标值那么left++,如果大于目标值那么right--,，直到left==right相遇即可结束，但是这些的前提是有序数列（升序）。

?好吧，这一个样例很凑巧，直接等于目标值。

?

算法原理：
    sort排序
    [left+right] === target  return {[left],[right]}
    [left+right] < target   left++
    [left+right] > target   right--

直到left==right相遇的时候就结束

这是我记录下来地一个笔记?：

?

第三步：代码实现

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) 
    {
        int left=0,right=price.size()-1;
        int sum=0;
        while(left<right)
        {
            sum=price[left]+price[right];
            if(sum>target)right--;
            else if(sum<target) left++;
            else return {price[left],price[right]};
        }
        return {-1,-1};
    }
};

🚩三数之和

本题链接——三数之和

?第一步：了解题意

我们要找nums数组中三个数相等等于0即可，每个三元组都是不重复的，比如[-1,0,1]和[0,1,-1]是重复的，只能取一组。

第二步：算法原理

上一个题目是利用双指针给有序数组求解俩数之和，这题是求三数之和也一样可以用双指针，但是不同的是，三数，怎么用俩个指针来控制呢？

思路：

• 1.先排序
• 2.固定一个a
• 3.在该数的后面区间内，利用“双指针”算法快速找到俩个数之和等于-a即可。

但是这一题并没有这么固定，我们需要处理2个小细节：

?不漏：

就是如果找到了符合题意的，但是指针不能停，还得继续缩小区间，比如

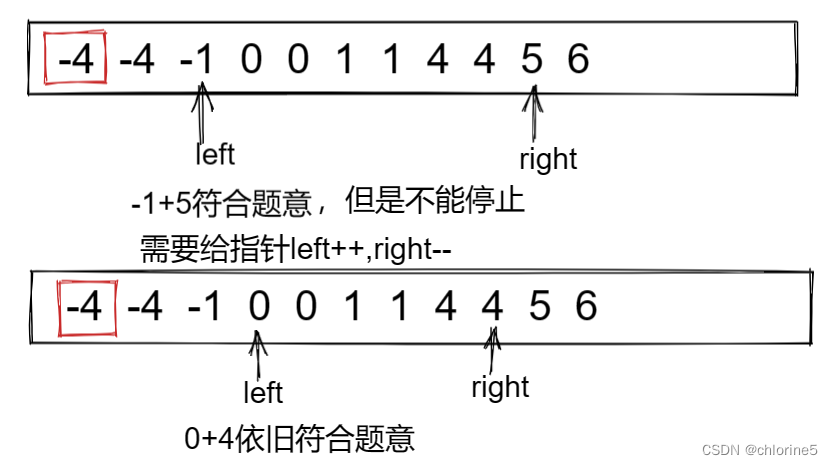
?去重:

大家可以理解去重其实也是一种优化，就是避开掉重复的运算。比如：

并且如果固定的a值，下一个固定的a值与原先的a值相等，也是可以跳过这次循环继续下下个固定a值。

！优化

我们首先都是要给有序数组排序的sort排成升序，那么固定的a值肯定是需要<=0的，不然如果a=0或者a>0，这个序列是升序，那么就代表着a后面的数据都是>0,那么肯定是不等相加等于0的。

所以只要满足a<=0即可。

第三步：代码实现

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) 
    {
        vector<vector<int>> ret;
        //排序
         sort(nums.begin(),nums.end());
         //利用双指针解决问题
        for(int i=0;i<nums.size()&&nums[i]<=0;i++)//固定a
        {
            if(i>0)//看看固定的a值是不是和原先的相等，相等就跳过下个一个值固定
            {
                 if(nums[i]==nums[i-1]) continue;
            }
            int left=i+1,right=nums.size()-1,a=nums[i];
            while(left<right)
            {
                if(nums[left]+nums[right]<-a)
                {
                    left++;
                    while(left<right&&nums[left]==nums[left-1])
                    {
                        left++;
                    }
                }
                else if(nums[left]+nums[right]>-a)
                {
                    right--;
                    while(left<right&&nums[right]==nums[right+1])
                    {
                        right--;
                    }
                }
                else
                {
                    ret.push_back({nums[i],nums[left],nums[right]});
                    left++;
                     while(left<right&&nums[left]==nums[left-1])
                    {
                        left++;
                    }
                    right--;
                    while(left<right&&nums[right]==nums[right+1])
                    {
                        right--;
                    }
                }
            }
        }
        return ret;
    }
};

?安静下来，慢慢地，一点一点地，与时间相遇。