频率域滤波图像复原之逆滤波的python实现——数字图像处理
逆滤波原理
逆滤波是一种在频率域进行的图像复原技术,常用于修复由运动模糊等因素引起的图像退化。具体步骤如下:
**频率域表示:**首先,将退化的图像通过傅里叶变换从空间域转换到频率域。这使得图像的频率成分变得明显,便于分析和处理。
**退化模型识别:**在频率域中,图像退化通常可以表示为原始图像与某个退化函数(比如运动模糊)的卷积。逆滤波需要识别这个退化函数,这通常需要一定的先验知识或假设。
**设计逆滤波器:**逆滤波器的设计基于退化函数的逆。如果已知或假设了退化函数的形式,那么可以计算其在频率域的逆。这个逆滤波器理论上可以完全抵消退化效果。
应用逆滤波器:将设计好的逆滤波器应用于退化图像。在频率域中,这通常表示为对退化图像的频率响应和逆滤波器的频率响应进行乘法操作。
逆傅里叶变换:处理完毕后,通过逆傅里叶变换将图像从频率域转换回空间域,得到复原后的图像。
然而,逆滤波也有其局限性。例如,当退化函数不是很精确时,或者图像包含噪声时,直接应用逆滤波可能会放大这些错误或噪声,导致复原效果不理想。因此,在实际应用中,逆滤波通常与其他技术(如威纳滤波)结合使用,以改善复原质量。
公式表示
设 H(u,v) 是已知的退化函数在频率域的表示,G(u,v) 是退化图像在频率域的表示,那么根据线性系统理论,退化过程可以表示为:
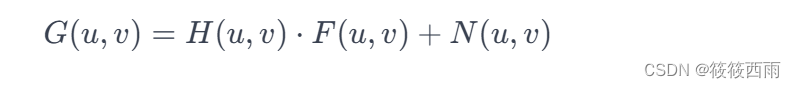
其中 ,F(u,v) 是原始图像在频率域的表示,N(u,v) 是加性噪声。
在理想情况下(忽略噪声),退化过程可以简化为:
G(u,v)=H(u,v)?F(u,v)
逆滤波的目的是通过逆转 H(u,v) 的影响来恢复 F(u,v)。如果 H(u,v) 是已知且没有零点,那么逆滤波器 H^-1 (u,v) 可以表示为:
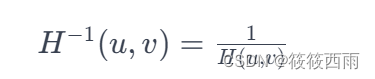
因此,复原图像 F^ (u,v) 可以通过逆滤波器处理退化图像 G(u,v) 来获得:
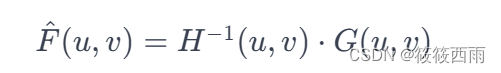
最后,通过对 F^(u,v) 进行逆傅里叶变换,可以得到空间域中的复原图像。
需要注意的是,当 H(u,v) 接近或等于零的时候,上述逆滤波器会放大噪声,这是逆滤波的主要局限性之一。在实际应用中,为了避免这种情况,通常会对逆滤波器进行一定的修改或者使用其他更加稳健的复原方法。
python实现下图

提示
这是一幅经过参数k=0.0025的大气湍流模型退化后的图像,。结果依次显示用不同截止半径限制频率后逆滤波得到的结果。,限制滤波频率是通过对比值G(u,v)/H(u,v)应用一个阶数为10的巴特沃斯低通函数来实现的,4幅结果图的截止频率分别为float(“inf”)(对应着全滤波)、40、60、70。
python代码
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('Fig0525.tif', 0)
rows = img.shape[0]
cols = img.shape[1]
Cx = rows//2
Cy = cols//2
dft = np.fft.fft2(img)
dft_shift = np.fft.fftshift(dft)
img_list = []
img_name_list = []
# 大气湍流模型的参数
k = 0.0025
# 构造退化函数
H = np.zeros((rows, cols))
for x in range(rows):
for y in range(cols):
D = ((x - Cx) ** 2 + (y - Cy) ** 2) ** (5/6)
H[x, y] = np.exp(-k * D)
# 构造巴特沃斯低通滤波器
radius = [float("inf"), 40, 60, 70]
n = 10
for D0 in radius:
HB = np.zeros((rows, cols))
for x in range(rows):
for y in range(cols):
D = np.sqrt((x-Cx)**2 + (y-Cy)**2)
HB[x, y] = 1 / (1 + (D/D0)**(2*n))
dft_filtered = np.multiply(np.multiply(dft_shift, 1/H), HB)
img_result = np.abs(np.fft.ifft2(np.fft.fftshift(dft_filtered)))
img_list.append(img_result)
img_name_list.append('r=' + str(D0))
_, axs = plt.subplots(2, 2)
for i in range(2):
for j in range(2):
axs[i, j].imshow(img_list[i * 2 + j], cmap='gray')
axs[i, j].set_title(img_name_list[i * 2 + j])
axs[i, j].axis('off')
#plt.savefig('inverse_filter.jpg')
plt.show()
结果展示

总结
图像复原是一种客观的操作,通过使用退化现象的先验知识重建或恢复一副退化的图像;图像在形成、传输和记录的过程中,由于受多种原因的影响,图像的质量会有下降,典型表现为图像模糊、失真、有噪声等,这一降质的过程称为图像的退化。而图像复原试图利用退化现象的某种先验知识(即退化模型),把已经退化了的图像加以重建和复原。其目的就是尽可能地减少或去除在获取图像过程中发的图像质量的下降(退化),恢复被退化图像的本来面目。
逆滤波复原过程:对退化的图像进行二位傅里叶变换;计算系统点扩散函数的二位傅里叶变换;引入H(fx,fy)计算并且对结果进行逆傅里叶变换。
逆滤波:简单的就是将退化函数去除,直接的逆滤波没有什么意义,只处理了靠近直流分量的部分,其他不做处理。如果加入巴特沃斯低通滤波器,效果会好点,可是在运动模糊的图片中就不好使了。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 一文详解Dockerfile自定义镜像
- 小白入门基础 - tomcat
- ThreadLocal用法以及使用场景
- 2024 年全球十大远程控制软件排行榜
- Go(Golang)的10个常见代码片段用于各种任务
- python对常见的激活函数绘图操作(详细代码讲解)
- 四、C++运算符(3)赋值运算符
- 基于ssm医院预约挂号系统的设计与实现论文
- 【Docker仓库】部署Docker Registry web-ui管理镜像仓库
- C++入门【32-C++ 数据结构】