计算机组成原理04：一位乘法

原码的一位乘法是基于加法设计的。回想我们在竖式计算乘法时，都是通过一个数与另外一个数的另外一位相乘，最后相加得到结果。计算机计算原码一位乘法也是一样的原理。这里就涉及到计算时一个非常重要的操作：数据移位。

原码乘法问题分析

1. 需要多输入的全加器
2. 假设乘数长度最长为n，需要长度为2n的积寄存器
3. 根据乘数不同的位，移位的次数不动

移位方式

在汇编语言中我们已经学过逻辑移位和算术移位的区别：其中，逻辑左移和算术左移式一样的，但逻辑右移会在左侧补0，而算术右移会在左侧复制符号位。

原码乘法算法设计

由于计算机原码都是二进制的，所以每次乘一位只存在加0还是加原来的数的问题，我们设计算法如下：

1. 确定符号位：由两个数的符号位求异或得到
2. 确定小数位数：由两者的小数位数相加
3. 从右往左乘，每乘完一位，将部分积相加并且右移一位，并将移出的位加入积寄存器
4. 重复3直到乘到最后一位，将所有部分积中的位数加入积寄存器。
5. 最后一次操作完，部分积不移位。

补码乘法算法设计

在计算机中，由于补码实际上比起原码更加常用，因此研究补码的一位乘法非常具有意义。但是补码在处理负数时和原码有很大的差别，因此补码乘法的算法和原码乘法算法有很大区别。

补码乘法的计算原理公式如下：

基于以上的公式，我们可以设计补码一位乘法。但是有一些需要特殊注意的问题：

1. i=n时，yi+1 = 0
2. yn+1可以在乘数寄存器的后面增加一位
3. 算术右移部分积与乘数寄存器
4. 被乘数均以双符号位参与运算

补码乘法的大致计算步骤和原码乘法大致相同，但是根据yi+1和yi的大小，每步计算有区别。也就是：如果yi+1<yi，那么部分积+[-X]补，如果yi+1=yi，部分积+0；如果yi+1>yi，那么部分积+[X]补。

下面是一个补码乘法的例子：

已知X=+1011，Y=+1101,用补码乘法求XY。

解：

已知[X]补=01011，[Y]补 = 01101 ，[-X]补 = 10101.


部分积            乘数            说明            结果
  00 0000
+ 11 0101        011010         yi+1<yi
-------------------------------------------------------
  110101
->111010         01101          yi+1>yi            1
+ 001011
--------------------------------------------------------
  000101
->000010         0110           yi+1<yi            11
+ 110101
--------------------------------------------------------
  110111         
->111011         011            yi+1=yi           111
+ 000000
--------------------------------------------------------
  111011
->111101         01             yi+1>yi           1111
+ 001011
--------------------------------------------------------
  001000       
->000100         0                结束            01111

故[XY]补= 0 01001111，[XY] = 0 0100 01111，即为+1000 1111，8FH.

乘法器的设计

这是一位乘法器的实现：

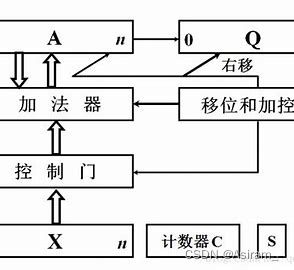
和加法器一样，这是阵列乘法器的设计

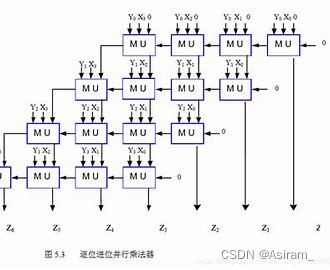
乘法器分为串行阵列，并行阵列和补码阵列。上面展示的是串行进位。同理，串行进位相比并行进位的时间比较慢，效率比较低，但是并行阵列需要更多的空间，更复杂的乘法器设计。