快速排序学习笔记

代码框架

    // 在数组nums将下标从left到right中进行从小到大排序
    // 原理是先将一个元素排好序，然后将其他的元素排好序
    void sort(int[] nums, int left, int right) {
        if (left >= right) {
            return;
        }
        // 对数组nums[left,right]进行切分，使得nums[left,p-1]<=nums[p]<=nums[p+1,right]
        int p = partition(nums, left, right);
        // 去左右数组进行切分
        sort(nums, left, p - 1);
        sort(nums, p - 1, right);
    }



    // 在数组中nums[left,right]中寻找到一个分界点p
    int partition(int[] nums, int left, int right) {
        // 将数组中最左边的元素放入正确的位置后，返回该位置
        int pivot = nums[left];
        // 最后数组被分为三个区间，[left,i)和i和(j,right]
        int i = left + 1, j = right;
        while (i <= j) {
            // i右移找大于pivot的数
            while (i < right && nums[i] <= pivot) {
                i++;
            }
            // j左移找到小于pivot的数
            while (j > left && nums[j] >= pivot) {
                j--;
            }
            // 判断此时的i和j是否越界
            if (i >= j) {
                break;
            }
            swap(nums, i, j);
        }
        // 最后将pivot和j进行交换
        swap(nums, left, j);
        return j;
    }

    // 将元素随机打乱
    void shuffle(int[] nums) {
        int len = nums.length;
        Random random = new Random();
        for (int i = 0; i < len; i++) {
            // 生成[i,len-1]之间的随机数
            int index = i + random.nextInt(len - i);
            swap(nums, i, index);
        }
    }

    void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

为什么要用shuffle将数组进行乱序处理？

目的是消除对初始输入的依赖，使得算法更具有随机性。在快排算法中，选择分区点的方式可能会影响算法的性能。如果数组已经有序或者近似有序，选择第一个元素作为分区点可能导致算法性能下降，因为分区点选择的不好可能导致快速选择算法的退化为O(n^2)的时间复杂度。

在快速排序中，`partition()` 会选择一个基准值（pivot），然后重新排列数组或列表的元素，使得小于基准值的元素都位于它的左侧，大于基准值的元素都位于它的右侧。通常，它返回一个索引值，表示基准值在排序后所在的位置，同时也将数组或列表划分成两个部分。

再这么看快排就很简单了，一直分割左右两块，直到所有都排序完为止。

注意base case是左应该<=右！

另外，其实对比可以发现出，快排和二叉树的前序遍历是很像的：

/* 二叉树遍历框架 */
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    /****** 前序位置 ******/
    print(root.val);
    /*********************/
    traverse(root.left);
    traverse(root.right);
}

一句话总结

快速排序是先将一个元素排好序，然后再将剩下的元素排好序。

快速排序的核心无疑是?`partition`?函数，?`partition`?函数的作用是在?`nums[lo..hi]`?中寻找一个切分点?`p`，通过交换元素使得?`nums[lo..p-1]`?都小于等于?`nums[p]`，且?`nums[p+1..hi]`?都大于?`nums[p]`：

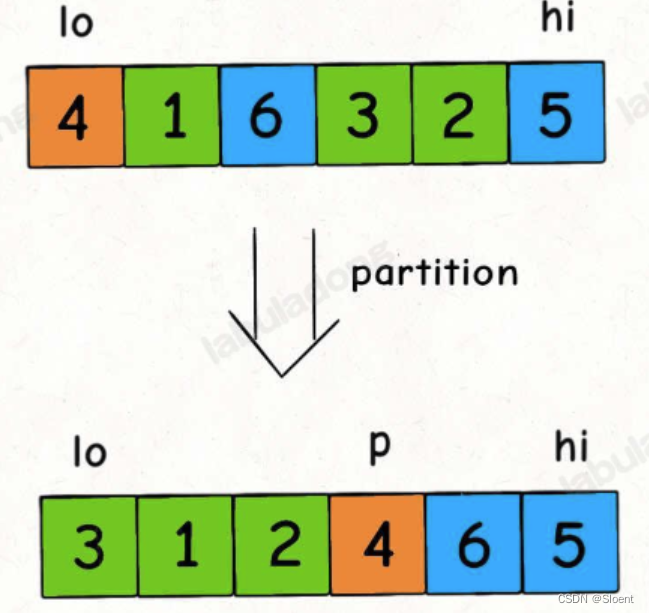
一个元素左边的元素都比它小，右边的元素都比它大，不就是它自己已经被放到正确的位置上了吗？

所以?`partition`?函数干的事情，其实就是把?`nums[p]`?这个元素排好序了。然后呢？你再把剩下的元素排好序不就得了。

剩下的元素有哪些？左边一坨，右边一坨，去吧，对子数组进行递归，用?`partition`?函数把剩下的元素也排好序。

从二叉树的视角，我们可以把子数组?`nums[lo..hi]`?理解成二叉树节点上的值，`sort`?函数理解成二叉树的遍历函数。

排序数组

912. 排序数组 - 力扣（LeetCode）

class Solution {
? ? public int[] sortArray(int[] nums) {
? ? ? ? shuffle(nums);
? ? ? ? quickSort(nums, 0, nums.length - 1);
? ? ? ? return nums;
? ? }

? ? void shuffle(int[] nums) {
? ? ? ? Random random = new Random();
? ? ? ? for (int i = 0; i < nums.length; i++) {
? ? ? ? ? ? int p = i + random.nextInt(nums.length - i);
? ? ? ? ? ? swap(nums, i, p);
? ? ? ? }
? ? }

? ? void quickSort(int[] nums, int left, int right) {
? ? ? ? if (left < right) {
? ? ? ? ? ? int pivot = partition(nums, left, right);
? ? ? ? ? ? // 分治，分别对左右的数据开始递归
? ? ? ? ? ? quickSort(nums, left, pivot - 1);
? ? ? ? ? ? quickSort(nums, pivot + 1, right);
? ? ? ? }
? ? }

? ? int partition(int[] nums, int left, int right) {
? ? ? ? int pivot = nums[left];
? ? ? ? int i = left + 1;
? ? ? ? int j = right;

? ? ? ? while (i <= j) {
? ? ? ? ? ? while (i <= right && nums[i] <= pivot) {
? ? ? ? ? ? ? ? i++;
? ? ? ? ? ? }
? ? ? ? ? ? while (j >= left && nums[j] > pivot) {
? ? ? ? ? ? ? ? j--;
? ? ? ? ? ? }

? ? ? ? ? ? if (i <= j) {
? ? ? ? ? ? ? ? swap(nums, i, j);
? ? ? ? ? ? }
? ? ? ? }
? ? ? ? swap(nums, left, j);
? ? ? ? return j;
? ? }

? ? void swap(int[] nums, int i, int j) {
? ? ? ? int temp = nums[i];
? ? ? ? nums[i] = nums[j];
? ? ? ? nums[j] = temp;
? ? }
}

数组中的第k个最大元素

215. 数组中的第K个最大元素 - 力扣（LeetCode）

class Solution {
  public int findKthLargest(int[] nums, int k) {
        shuffle(nums);
        int left = 0, right = nums.length - 1;
        // 因为是找第 k 大的元素，而不是找第 k 小的元素，所以要从右边开始数 k 个
        k = nums.length - k;
        while (left <= right) {
            int p = partition(nums, left, right);
            // 缩小查找范围
            if (p < k) {
	            // 说明第k大的元素在分区右边
                left = p + 1;
            } else if (p > k) {
	            // 说明第k大的元素在分区左边
                right = p - 1;
            } else {
                return nums[p];
            }
        }
        // 未找到
        return -1;
    }
    
    void shuffle(int[] nums) {
        Random random = new Random();
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            int r = i + random.nextInt(n-i);
            swap(nums, i, r);
        }
    }
    
    int partition(int[] nums, int left, int right) {
        int p = nums[left], i = left + 1, j = right;
        while (i <= j) {
	        // `i` 向右移动，找到第一个大于 `p` 的元素
            while (i <= right && nums[i] <= p) i++;
            // `j` 向左移动，找到第一个小于等于 `p` 的元素
            while (j >= left && nums[j] > p) j--;
            if (i >= j) break;
            // 如果左区间有比 p 大的数，右区间有比 p 小的数，且下标左小于右，交换i与j
            swap(nums, i, j);
        }
        // 最后，将 `nums[left]`（即分区点原始位置）与 `nums[j]` 交换，将分区点放到正确的位置。
        swap(nums, left, j);
        // 返回分区点索引
        return j;
    }

    void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

补充：

优先级队列做法

class Solution {
    public int findKthLargest(int[] nums, int k) {
        // 利用优先级队列，自动是小根堆
        PriorityQueue<Integer> queue = new PriorityQueue<>();
        for (int i = 0; i < k; i++) {
            queue.add(nums[i]);
        }
        for (int i = k; i < nums.length; i++) {
            if (nums[i] > queue.peek()) {
                queue.poll();
                queue.add(nums[i]);
            }
        }
        return queue.peek();
    }
}