算法设计与分析实验报告-分支限界法

?校课程的简单实验报告。

算法设计与分析实验报告-递归与分治策略

算法设计与分析实验报告-动态规划算法

算法设计与分析实验报告-贪心算法

????????dijkstra迪杰斯特拉算法（邻接表法）

算法设计与分析实验报告-回溯法

算法设计与分析实验报告-分支限界法

算法设计与分析实验报告-分治法相关练题

北京大学出版社-算法设计与分析

---

一、实验目的

1.掌握分支限界法的基本思想及搜索方式；

2.掌握分支限界法的算法框架；

3.掌握分支限界法的基本应用。

二、实验内容

使用分支限界法求解以下问题，要求给出程序代码，并编译运行程序：

1.P192习题1。

? ? ? ? 一辆载重量为C的卡车，给定n头奶牛，输入每头奶牛的重量和产奶量，尽可能装入更多的奶牛，使单位重量的产奶量最佳。

三、实验环境

1. 使用的操作系统及版本：

Windows 10

2. 使用的编译系统及版本：

CLion 2022.2.4

四、实验步骤及说明

????????实际上是01背包问题的分支限界法。

代码如下：

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
struct cow{
    int w; // 奶牛重量
    int v; // 奶牛产奶量
    double k; // 单位重量奶牛产奶量

    cow(){
        w = 1, v = 0;
    };

    void getk(){
        k = (double ) v / w;
    }

//    bool operator<(const cow& r) const{ //运算符重载 sort排序时使用
//        return k < r.k;
//    }
};
// sort 降序排序时使用
bool cmp(cow a, cow b){
    return a.k > b.k;
}

struct node{ // 树节点
    int ws; // 到当前节点时的总质量
    int vs; // 到当前节点时的总产奶量
    int upBound; // 上界
//    node* parent;
//    int level; // 层级，n为叶子（根节点为0层）
//    int lChild; // 是否是左孩子（1是）
    int index;
    int a[100];
    node() : a(){
        ws = 0, vs = 0, upBound = 0, index = 0;
    }

    bool operator<(const node& r) const{ // 运算符重载， 大顶堆使用（根据上界upBound降序）
        return upBound < r.upBound;
    }

    // 上界函数，假设所有奶牛已按 单位质量产奶量 降序排序
    // 尽可能把还能完整装载的奶牛进行选择，最后再选择 单位产奶量 * 剩余载重量， 填满货车。
    void getBound(int C, int n, vector<cow> cows){
        int restW = C - ws; // 剩余可选择的载重量
        int i = index;
        double tmpV = vs;
        // 贪心策略, 尽可能选择最大且完整
        while(i < n && cows[i].w <= restW){
            restW -= cows[i].w;
            tmpV += cows[i].v;
            i++;
        }

        if(i < n){
            tmpV += cows[i].k * restW;
        }
        upBound = tmpV;
    }
};
int main(){
    int C = 0, n = 0;
    cin >> n >> C;
    vector<cow> cows;
    for(int i = 0; i < n; i ++){
        cow tmp;
        cin >> tmp.w >> tmp.v;
        cows.emplace_back(tmp);
        cows[i].getk();
    }
    sort(cows.begin(), cows.end(), cmp); // 按单位质量产奶量进行排序
//    for(auto &x:cows){
//        cout << x.k << ' ';
//    }
    priority_queue<node> q;
    // 初始化根节点
    node t;
    t.getBound(C, n, cows);
    q.push(t);

    int result = 0;//最优解
    node bestNode;
    while (!q.empty()) {
        node f = q.top();
        q.pop();

        //得到最优解
        if(f.vs >= f.upBound){
            result = f.vs;
            bestNode = f;
            break;
        }
        //构造左结点（不选择-0）
        if (f.index < n) {
            node l = f;
            l.index = l.index + 1;
            l.getBound(C, n, cows);
            q.push(l);
        }
        //构造右结点（选择-1）
        if (f.index < n && f.ws + cows[f.index].w <= C) {
            node r = f;
            r.ws += cows[r.index].w;
            r.vs += cows[r.index].v;
            r.a[r.index] = 1;
            r.index = r.index + 1;
            r.getBound(C, n, cows);

            q.push(r);
        }
    }

    cout << result << endl;
    cout << "选择第";
    for(int i = 0; i < n; i ++) if(bestNode.a[i]) cout << i + 1 << "头 ";
    cout << "奶牛装入车中。" << endl;
    return 0;
}

测试如下：

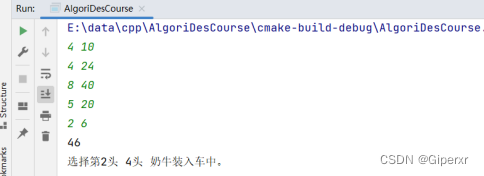
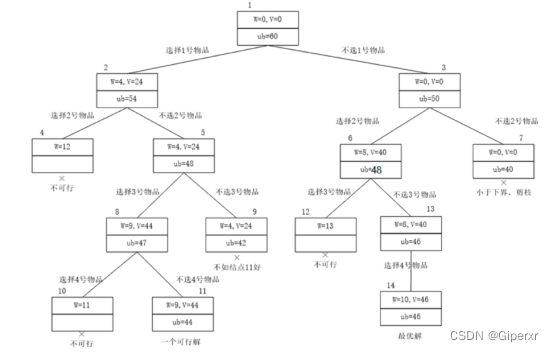
五、实验小结及思考

通过本次实验掌握分支限界法的基本思想及搜索方式、掌握分支限界法的算法框架、掌握分支限界法的基本应用。