10 种最佳排序算法原理及代码

什么是排序算法?
? ? 从本质上讲,排序算法是一种计算机程序,它将数据组织成特定的顺序,例如字母顺序或数字顺序,通常是升序或降序。
排序算法能干啥?
排序算法主要用于以有效的方式重新排列大量数据,以便更容易地进行搜索和操作。它们也被用于提高其他算法的效率,如搜索和合并,这些算法依赖于排序的数据进行操作。
为什么排序算法如此重要?
排序算法用于按特定顺序组织数据,这使得搜索、访问和分析更容易。在许多应用中,排序是数据处理管道的关键部分,排序算法的效率会对系统的整体性能产生重大影响。
-
数据库:排序用于按特定顺序检索记录,例如按日期、字母顺序或数字顺序。这使用户能够快速找到所需的数据,而无需手动搜索大量未排序的数据。
-
搜索引擎:按相关性顺序对搜索结果进行排序。通过以这种方式对结果进行排序,用户可以快速找到他们正在寻找的信息,而无需筛选不相关或不相关的结果。
-
许多科学和工程应用中:研究人员可以进行数据分析和模拟,以深入了解复杂系统,并对未来行为做出更准确的预测。
数据结构中不同类型的排序
有各种类型的排序可用。排序算法的选择取决于各种因素,例如数据集的大小、排序的数据类型以及所需的时间和空间复杂度。
基于比较的排序算法
这些算法比较数据集的元素,并根据比较结果确定它们的顺序。基于比较的排序算法包括冒泡排序、插入排序、快速排序、归并排序和堆排序。
非基于比较的排序算法
这些算法不直接比较元素,而是使用数据集的其他属性来确定它们的顺序。非基于比较的排序算法包括计数排序、基数排序和桶排序。
原地排序算法
这些算法对数据集进行就地排序,这意味着它们不需要额外的内存来存储中间结果。就地排序算法的包括冒泡排序、插入排序、快速排序和 shell 排序。
稳定的排序算法
这些算法保持数据集中相等元素的相对顺序。稳定排序算法的包括插入排序、归并排序和?Timsort。
自适应排序算法
这些算法利用数据集中的任何现有顺序来提高效率。自适应排序算法包括插入排序、冒泡排序和Timsort。
你需要知道的 10 大排序算法
1. 冒泡排序
冒泡排序是一种简单的排序算法,它重复遍历给定的数据列表,比较每一对相邻的数据,如果它们的顺序不对,就交换它们。该算法一直持续到遍历整个列表而不交换任何项。
冒泡排序有时也被称为“下沉排序”。
 ?
?
从列表的开头开始,比较每个相邻的对,如果它们的顺序不对,交换它们的位置(后一个比前一个小)。每次迭代之后,需要比较的元素(最后一个)会减少一个,直到没有其他元素需要比较为止。?
冒泡排序的历史
冒泡排序的起源可以追溯到 20 世纪 50 年代末,唐纳德·高德纳(Donald Knuth)在他 1968 年的经典著作《计算机编程的艺术》中普及了它。
从那时起,它被广泛应用于各种应用程序中,包括编译器的排序算法、数据库中的元素排序,甚至扑克牌排序。
气泡排序的优缺点
冒泡排序被认为是一种相对低效的排序算法,因为它的平均复杂度和最坏情况复杂度都是 O(n^2)。这使得它比大多数其他排序算法(如快速排序或归并排序)效率低得多。
说明: O(n^2) 复杂度意味着算法完成所需的时间与输入大小的平方成正比。这意味着较大的输入大小会导致算法花费更长的时间来完成。
例如,如果考虑对数字数组进行排序的算法,对包含 10 个数字的数组进行排序可能需要 1 秒,但对包含 20 个数字的数组进行排序可能需要 4 秒。这是因为算法必须将数组中的每个元素与其他元素进行比较,因此对于较大的数组必须进行 20 次比较,而对于较小的数组只需进行 10 次比较。
然而,它非常容易理解和实现,并且经常被用作排序的入门和更复杂算法的基础。但现在很少在实际中使用了。
冒泡排序的用处
冒泡排序是一种简单的算法,可用于对小列表或元素数组进行排序。它易于实现和理解,因此可以在简单性和清晰度比性能更重要的情况下使用。
-
教学:它经常在计算机科学课程中用作简单排序算法的示例。学生可以通过学习气泡排序来学习基本的排序技术并了解算法的工作原理。
-
对小型数据集进行排序:它可用于对多达几百个元素的小型数据集进行排序。在性能不是关键问题的情况下,气泡排序可以成为对小列表进行排序的一种快速简便的方法。
-
对数据进行预排序:它可以用作更复杂的排序算法的初步步骤。例如,如果数据已部分排序,则可以在运行更复杂的算法之前使用气泡排序对数据进行进一步排序。
-
使用有限的资源对数据进行排序:它在资源有限的情况下很有用,例如在嵌入式系统或微控制器中,因为它需要很少的内存和处理能力。
-
用于更复杂算法的基础:它通常与归并排序或快速排序结合使用,并使用插入排序对小的子数组进行排序,因为这些算法可以在较大的数据集上获得更好的性能。
冒泡排序实现
- 使用嵌套循环遍历项。
- 比较列表中相邻的项。
- 如果它们的顺序不对,就交换它们。
- 继续,直到列表排序完毕。
Python 冒泡排序代码示例
def bubble_sort(items):
for i in range(len(items)):
for j in range(len(items)-1-i):
if items[j] > items[j+1]:
items[j], items[j+1] = items[j+1], items[j]
return items
items = [6,20,8,19,56,23,87,41,49,53]
print(bubble_sort(items))JavaScript 冒泡排序代码示例
function bubbleSort(items) {
let swapped;
do {
swapped = false;
for (let i = 0; i < items.length - 1; i++) {
if (items[i] > items[i + 1]) {
let temp = items[i];
items[i] = items[i + 1];
items[i + 1] = temp;
swapped = true;
}
}
} while (swapped);
return items;
}
let items = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53];
console.log(bubbleSort(items));2. 插入排序
插入排序是另一种简单的算法,它一次构建一个最终排序的数组,它之所以这样命名是因为其较小的元素被插入到排序数组的正确位置。
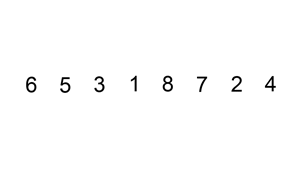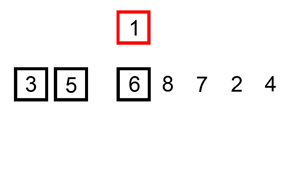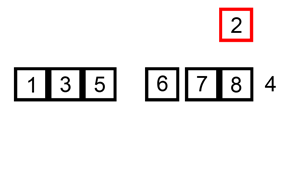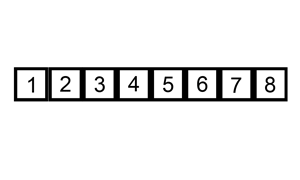 ?
?
不完全排序列表最初只包含列表中的第一个元素。在每次迭代中,从“尚未检查顺序”的输入数据中删除一个元素,并将其插入已排序的列表中。
插入排序的历史
在《计算机程序设计的艺术》一书中,Knuth 评论说,插入排序“早在 1946 年 John Mauchly 就在第一次发表的关于计算机排序的讨论中提到”,并将其描述为一种易于理解和实现的“自然”算法。
到 20 世纪 50 年代末,Donald L. Shell对他的 shell 排序方法进行了一系列改进(下文将介绍),该方法比较被每次传递的距离减小的元素,从而将算法的复杂性降低到?O(n^{3/2}) 和 O(n^{4/3}) 。这听起来可能不多,但对于实际应用来说,这是一个相当大的改进!
说明:?O(n^{3/2}) 和 O(n^{4/3}) ?复杂度比 O(n^2)?复杂度更有效,这意味着它们需要更少的时间来完成。这是因为它们不需要像复杂度 O(n^2)?那样执行那么多比较。
例如,使用 O(n^2) 算法对十个数字的数组进行排序可能需要 1 秒,但使用 O(n^{3/2}) 算法对相同的数组进行排序可能需要 0.5 秒。这是因为当使用 O(n^{3/2}) 算法时,算法可以执行更少的比较,从而导致更快的运行时间。
2006年,Bender, Martin Farach-Colton 和 Mosteiro 发表了插入排序的一个新变体,称为库排序或“间隙插入排序”,它在整个数组中留下少量未使用的空间(或“间隙”),进一步将运行时间提高到 O(nlogn)。
说明: O(nlogn)?时间复杂度比 O(n^2),O(n^{3/2}) 和 O(n^{4/3})?时间复杂度更有效。这是因为它使用了分而治之的方法,这意味着它可以将问题分解成更小的部分,并更快地解决它们。
例如,使用 O(n^2) 算法对十个数字的数组进行排序可能需要 1 秒,使用 O(n^{3/2}) 算法对相同的数组进行排序可能需要 0.5 秒,但使用 O(nlogn)?算法对相同的数组进行排序可能需要 0.1 秒。这是因为该算法可以将数组分解成更小的部分,并并行求解它们,从而加快运行时间。
插入排序的优缺点
插入排序通常在实际中用于小数据集或作为更复杂算法的基础。
和冒泡排序一样,它的最坏情况和平均情况的时间复杂度是 O(n^2)。但与冒泡排序不同的是,插入排序可以用于对数据集进行就地排序,这意味着它不需要额外的内存来存储中间结果。
插入排序的用处
插入排序简单而高效,通常用于输入数据已经部分排序的情况,或者输入数据的大小相对较小的情况。它也用于对小数据集进行排序,以及为更复杂的算法基础,就像冒泡排序一样。
-
部分排序的数据:它非常适合数据已部分排序的情况。在这种情况下,算法可以快速将新元素插入到正确的位置,而无需进行复杂的排序操作。
-
在线排序:它通常用于输入数据事先未知的在线排序应用程序。在这些情况下,算法可以在接收到输入数据时对输入数据进行增量排序。
-
自适应排序:插入排序是自适应排序的候选方案,因为它可以利用输入数据中的现有顺序。随着输入数据变得更加有序,算法的性能也会提高。
插入排序实现
- 取一个未排序的列表,选择第一项作为“支点”。
- 遍历列表,将支点插入已排序列表中的正确位置。
- 对列表中的下一项重复此过程。
- 继续,直到列表排序完毕。
Python 插入排序代码示例
def insertion_sort(items):
for i in range(1, len(items)):
j = i
while j > 0 and items[j-1] > items[j]:
items[j-1], items[j] = items[j], items[j-1]
j -= 1
return items
items = [6,20,8,19,56,23,87,41,49,53]
print(insertion_sort(items))Javascript 插入排序代码示例
function insertionSort(items) {
for (let i = 1; i < items.length; i++) {
let j = i;
while (j > 0 && items[j - 1] > items[j]) {
let temp = items[j];
items[j] = items[j - 1];
items[j - 1] = temp;
j--;
}
}
return items;
}
let items = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53];
console.log(insertionSort(items));3. 快速排序
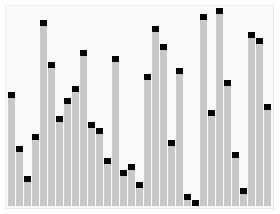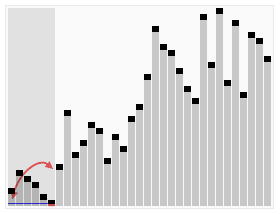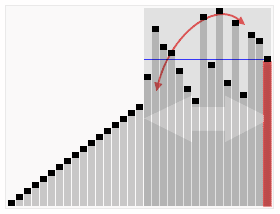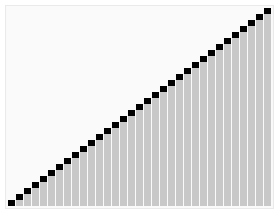
快速排序是一种流行的分治排序算法,它基于将数组划分为两个子数组的原则:一个包含比“支点”元素小的元素,另一个包含比支点元素大的元素。然后对这两个子数组进行递归排序。
快速排序的基本步骤包括:
- 从数组中选择一个支点元素。
- 将数组划分为两个子数组,一个包含比支点小的元素,另一个包含比支点大的元素。
- 使用快速排序对两个子数组进行递归排序。
- 组合两个已排序的子数组。
 ?
?
快速排序历史
快速排序是 1959 年由托尼·霍尔(Tony Hoare)发明的。霍尔在英国艾略特兄弟计算机公司工作时,开发了一种算法,用于在费兰蒂马克 1 号计算机的内存中对单词进行排序。
快速排序最初是在 1961 年作为一篇研究论文发表的,由于其简单、高效和易于实现,它迅速成为使用最广泛的排序算法之一。
快速排序的优点
- 它的平均时间复杂度为 O(nlogn)。
- 它只需要很少的额外内存,因为它对数组进行了排序。
- 它很容易实现并且被广泛理解。
- 它很容易被并行化。
快速排序的缺点
它的最坏情况下的时间复杂度是当主节点选择得不好时,在某些情况下,它比其他算法(如归并排序或堆排序)效率低 O(n^2)。
说明: 我们不想选择一个太小或太大的支点,否则算法将在二次时间内运行。理想情况是选择中位数作为支点,除非我们对数据分布有先验知识,否则,这并非易事。
快速排序的用处
快速排序作为一种高效的排序算法,有着广泛的应用。
-
大型数据集:它的平均情况时间复杂度为?O(nlogn),这意味着它可以快速对大量数据进行排序。
-
随机数据:它在随机排序的数据上表现良好,因为它依赖于 pivot 元素将数据分成两个子数组,然后递归排序。当数据是随机的时,透视元素可能接近中位数,从而获得良好的性能。
-
并行处理:它可以很容易地并行化,这使其成为在多核处理器上对大型数据集进行排序的理想选择。通过将数据划分为更小的子阵列,该算法可以同时在多个内核上执行,从而实现更快的性能。
-
外部排序:它通常用作外部排序算法的一部分,该算法用于对太大而无法放入内存的数据进行排序。在这种情况下,数据被分类为块,然后使用合并排序算法进行合并。
-
数据压缩:它用于一些数据压缩算法,例如?bzip2 压缩软件中使用的?Burrows-Wheeler 变换。该算法用于对 Burrows-Wheeler 矩阵中的数据进行排序,然后对其进行转换以生成压缩数据。
快速排序的实现
- 使用一个“支点”,最好是中位数,将列表分成两部分。
- 快速将左部分和右部分进行排序。
- 继续,直到列表排序完毕。
Python 快速排序代码示例
def quick_sort(items):
if len(items) > 1:
pivot = items[0]
left = [i for i in items[1:] if i < pivot]
right = [i for i in items[1:] if i >= pivot]
return quick_sort(left) + [pivot] + quick_sort(right)
else:
return items
items = [6,20,8,19,56,23,87,41,49,53]
print(quick_sort(items))Javascript 快速排序代码示例
function quickSort(items) {
if (items.length > 1) {
let pivot = items[0];
let left = [];
let right = [];
for (let i = 1; i < items.length; i++) {
if (items[i] < pivot) {
left.push(items[i]);
} else {
right.push(items[i]);
}
}
return quickSort(left).concat(pivot, quickSort(right));
} else {
return items;
}
}
let items = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53];
console.log(quickSort(items));4. 桶排序
桶排序是一种对均匀分布的数据进行排序的有用算法,它可以很容易地并行化以提高性能。
桶排序的基本步骤包括:
- 创建一个空桶数组。
- 根据定义的函数将输入数据分散到桶中。
- 使用另一种算法或递归地使用桶排序对每个桶进行排序。
- 将每个桶中排序的元素收集到原始数组中
 ?
?
元素被分配到各个 bin 中,然后在每个 bin 中对元素进行排序。
桶排序的历史
桶排序在 20 世纪50年代就已经实现了,有消息称这种方法在 20 世纪 40 年代就已经出现了。
不管怎样,如今它仍在广泛使用。
桶排序的优点
- 它对于均匀分布的数据是有效的,平均情况的时间复杂度为 O(n+k),其中 n 为元素的数量, k?为存储桶的数量。
- 它可以很容易地并行化,从而利用现代处理器中的多核。
- 它是稳定的,这意味着它保留了原始数组中相等元素的相对顺序。
- 它可以通过调整桶函数用于非均匀分布的数据。
说明:?O(n+k)?时间复杂度 O(n^2)、O(n^{3/2})、O(n^{4/3}) 和 O(nlogn)?更有效。这是因为它只需要执行线性数量的操作,而不管输入的大小。
例如,考虑一个对数字数组排序的算法。使用 O(n^2) 算法对一个包含十个数字的数组进行排序可能需要 1 秒,使用 O(n^{3/2}) 算法对同一个数组进行排序可能需要 0.5 秒,使用 O(nlogn) 算法对同一个数组进行排序可能需要 0.1 秒,但是 O(n+k) 使用算法对同一个数组进行排序可能需要 0.05秒。这是因为该算法不需要执行那么多比较。
桶排序的缺点
对于非均匀分布的数据,桶排序的效率低于其他排序算法,最坏情况下的性能为 O(n^2)。此外,它需要额外的内存来存储桶,这对于非常大的数据集来说可能是一个问题。
桶排序的用处
就像快速排序一样,桶排序可以很容易地并行化并用于外部排序,但是桶排序在处理均匀分布的数据时特别有用。
-
对浮点数进行排序:在这种情况下,范围被划分为固定数量的存储桶,每个存储桶代表输入数据的一个子范围。然后将数字放入相应的存储桶中,并使用另一种算法(例如插入排序)进行排序。最后,将排序后的数据连接成一个数组。
-
对字符串进行排序:字符串根据字符串的第一个字母分组到存储桶中。然后,使用另一种算法对每个存储桶中的字符串进行排序,或使用存储桶排序进行递归排序。对字符串中的每个后续字母重复此过程,直到对整个集合进行排序。
-
直方图生成:这可用于生成数据直方图,直方图用于表示一组值的频率分布。在这种情况下,将数据范围划分为固定数量的存储桶,并计算每个存储桶中的值个数。生成的直方图可用于可视化数据的分布。
桶排序的实现
- 将列表分成“桶”。
- 每个桶使用不同的排序算法进行排序。
- 然后将桶合并回一个排序列表。
Python 桶排序代码示例
def bucket_sort(items):
buckets = [[] for _ in range(len(items))]
for item in items:
bucket = int(item/len(items))
buckets[bucket].append(item)
for bucket in buckets:
bucket.sort()
return [item for bucket in buckets for item in bucket]
items = [6,20,8,19,56,23,87,41,49,53]
print(bucket_sort(items))Javascript 桶排序代码示例
function bucketSort(items) {
let buckets = new Array(items.length);
for (let i = 0; i < buckets.length; i++) {
buckets[i] = [];
}
for (let j = 0; j < items.length; j++) {
let bucket = Math.floor(items[j] / items.length);
buckets[bucket].push(items[j]);
}
for (let k = 0; k < buckets.length; k++) {
buckets[k].sort();
}
return [].concat(...buckets);
}
let items = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53];
console.log(bucketSort(items));5. Shell 排序
Shell 排序使用插入排序算法,但不是一次对整个列表排序,而是将列表分成更小的子列表。然后使用插入排序算法对这些子列表进行排序,从而减少排序列表所需的交换次数。
它的工作原理是首先定义一个称为增量序列的整数序列。增量序列用于确定将独立排序的子列表的大小。最常用的增量序列是“Knuth序列”,其定义如下(其中 h 为具有初始值的区间,n是列表的长度):
h = 1
while h < n:
h = 3*h + 1一旦定义了自增序列,Shell 排序算法就会对元素的子列表进行排序。子列表使用插入排序算法排序,以增量序列作为步长。该算法对子列表进行排序,从最大的增量开始,然后迭代到最小的增量。
该算法在增量大小为 1 时停止,此时它相当于常规的插入排序算法。
 ?
?
Shell 排序的历史
Shell排序是由 Donald Shell 于 1959 年发明的,是插入排序的一种变体,旨在通过将原始列表分解成更小的子列表并对这些子列表独立排序来提高其性能。
Shell 排序的优点
- 它是插入排序的泛化,因此易于理解和实现。
- 它的时间复杂度比很多输入数据序列?O(n^2)?都要好。
- 它是一种就地排序算法,这意味着它不需要额外的内存。
Shell 排序的缺点
很难预测 Shell 排序的时间复杂度,因为它取决于增量序列的选择。
Shell 排序的用处
Shell 排序是一种通用算法,用于在各种应用程序中对数据进行排序,特别是在对大型数据集(利用快速排序和桶排序)进行排序时。
-
对主要排序的数据进行排序:Shell 排序减少了对数据进行排序所需的比较和交换次数。这使得它比其他排序算法(如快速排序或归并排序)在特定情况下更快。
-
对具有少量反转的数组进行排序:反转是衡量数组未排序程度的指标,定义为顺序错误的元素对数。在对具有少量反转的数组进行排序时,Shell 排序比其他一些算法(如冒泡排序或插入排序)更有效。
-
就地排序:Shell 排序不需要额外的内存来对输入进行排序,使其成为就地排序的竞争者。这使得它在内存有限或不需要额外内存使用的情况下很有用。
-
在分布式环境中进行排序:通过将输入数据划分为较小的子列表并独立排序,可以在单独的处理器或节点上对每个子列表进行排序,从而减少对数据进行排序所需的时间。
Shell 排序的实现
Python Shell 排序代码示例
def shell_sort(items):
sublistcount = len(items)//2
while sublistcount > 0:
for start in range(sublistcount):
gap_insertion_sort(items, start, sublistcount)
sublistcount = sublistcount // 2
return items
def gap_insertion_sort(items, start, gap):
for i in range(start+gap, len(items), gap):
currentvalue = items[i]
position = i
while position >= gap and items[position-gap] > currentvalue:
items[position] = items[position-gap]
position = position-gap
items[position] = currentvalue
items = [6,20,8,19,56,23,87,41,49,53]
print(shell_sort(items))Javascript Shell 排序代码示例
function shellSort(items) {
let sublistcount = Math.floor(items.length / 2);
while (sublistcount > 0) {
for (let start = 0; start < sublistcount; start++) {
gapInsertionSort(items, start, sublistcount);
}
sublistcount = Math.floor(sublistcount / 2);
}
return items;
}
function gapInsertionSort(items, start, gap) {
for (let i = start + gap; i < items.length; i += gap) {
let currentValue = items[i];
let position = i;
while (position >= gap && items[position - gap] > currentValue) {
items[position] = items[position - gap];
position = position - gap;
}
items[position] = currentValue;
}
}
let items = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53];
console.log(shellSort(items));6. 归并排序
归并排序的基本思想是将输入列表分成两半,使用归并排序对每一半进行递归排序,然后将已排序的两半合并回一起。合并步骤是通过重复比较每一半的第一个元素并将两个元素中较小的元素添加到排序列表中来执行的。这个过程不断重复,直到所有的元素都合并在一起。
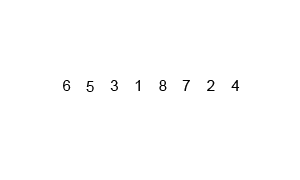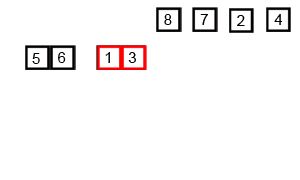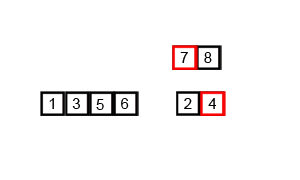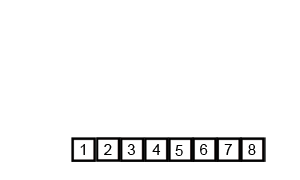 ?
?
- 首先,将列表划分为最小的单元(一个元素),
- 然后将每个元素与相邻列表进行比较,对两个相邻列表进行排序和合并。
- 最后,对所有元素进行排序和合并。
归并排序的历史
归并排序是由约翰·冯·诺伊曼于 1945 年发明的,作为一种基于比较的排序算法,它通过将输入列表划分为更小的子列表,对这些子列表进行递归排序,然后将它们合并在一起产生最终排序列表。
归并排序的优点
在最坏的情况下,归并排序的时间复杂度为O(nlogn),这使得它比冒泡排序、插入排序或选择排序等其他流行的排序算法更有效。
归并排序也是一种算法,这意味着它保留相等元素的相对顺序。
归并排序的缺点
归并排序在内存使用方面有一些缺点。该算法在除法步骤中需要额外的内存来存储列表的两半,在合并步骤中需要额外的内存来存储最终排序的列表。在对非常大的列表进行排序时,这可能是一个问题。
归并排序的用处
归并排序是一种通用排序算法,可以并行化排序大型数据集和外部排序(如快速排序和桶排序),它也通常用作更复杂算法(如冒泡排序和插入排序)的基础。
-
稳定的排序:合并排序的稳定排序意味着它保留了相等元素的相对顺序。这使得它在保持相等元素的顺序很重要的情况下很有用,例如在金融应用程序中或出于可视化目的对数据进行排序时。
-
实现二进制搜索:它用于有效地搜索排序列表中的特定元素,因为它依赖于排序的输入。合并排序可用于有效地对二进制搜索和其他类似算法的输入进行排序。
归并排序的实现
- 使用递归将列表拆分为更小的排序子列表。
- 将子列表重新合并在一起,在合并时对项目进行比较和排序。
Python 归并排序代码示例
def merge_sort(items):
if len(items) <= 1:
return items
mid = len(items) // 2
left = items[:mid]
right = items[mid:]
left = merge_sort(left)
right = merge_sort(right)
return merge(left, right)
def merge(left, right):
merged = []
left_index = 0
right_index = 0
while left_index < len(left) and right_index < len(right):
if left[left_index] > right[right_index]:
merged.append(right[right_index])
right_index += 1
else:
merged.append(left[left_index])
left_index += 1
merged += left[left_index:]
merged += right[right_index:]
return merged
items = [6,20,8,19,56,23,87,41,49,53]
print(merge_sort(items))Javascript 归并排序代码示例
function mergeSort(items) {
if (items.length <= 1) {
return items;
}
let mid = Math.floor(items.length / 2);
let left = items.slice(0, mid);
let right = items.slice(mid);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
let merged = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] > right[rightIndex]) {
merged.push(right[rightIndex]);
rightIndex++;
} else {
merged.push(left[leftIndex]);
leftIndex++;
}
}
return merged.concat(left.slice(leftIndex)).concat(right.slice(rightIndex));
}
let items = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53];
console.log(mergeSort(items));7. 选择排序
选择排序反复从列表的未排序部分中选择最小的元素,并将其与未排序部分的第一个元素交换。这个过程一直持续到整个列表排序完毕。
 ?
?
红色是当前最小值,黄色是排序列表,蓝色是当前项目。
选择排序的历史
选择排序是一种简单而直观的排序算法,从计算机科学的早期开始就存在了。类似的算法很可能是在 20 世纪 50 年代由研究人员独立开发的。
它是最早开发的排序算法之一,并且它仍然是用于教育目的和简单排序任务的流行算法。
选择排序的优点
选择排序在某些应用程序中使用,在这些应用程序中,简单性和易于实现比效率更重要。它还可以作为一种教学工具,用于向学生介绍排序算法及其属性,因为它易于理解和实现。
选择排序的缺点
尽管它很简单,但与其他排序算法(如归并排序或快速排序)相比,选择排序不是很有效。它的最坏情况下的时间复杂度为 O(n^2),对大列表进行排序可能需要很长时间。
选择排序也不是一种稳定的排序算法,这意味着它可能无法保持相等元素的顺序。
选择排序的用处
选择排序类似于冒泡排序和插入排序,因为它可以用来对小数据集进行排序,而且它的简单性也使它成为教育和学习排序算法的有用工具。其他用途包括:
-
使用有限的内存对数据进行排序:它只需要恒定量的额外内存来执行排序,因此在内存使用有限的情况下很有用。
-
使用唯一值对数据进行排序:它不依赖于主要排序的输入,因此对于具有唯一值的数据集来说,它是一个不错的选择,而其他排序算法可能必须执行额外的检查或优化。
选择排序的实现
- 遍历列表,选择最小的项。
- 将最小的项与当前位置项交换。
- 对列表的其余部分重复此过程。
?Python 选择排序代码示例
def selection_sort(items):
for i in range(len(items)):
min_idx = i
for j in range(i+1, len(items)):
if items[min_idx] > items[j]:
min_idx = j
items[i], items[min_idx] = items[min_idx], items[i]
return items
items = [6,20,8,19,56,23,87,41,49,53]
print(selection_sort(items))Javascript 选择排序代码示例
function selectionSort(items) {
let minIdx;
for (let i = 0; i < items.length; i++) {
minIdx = i;
for (let j = i + 1; j < items.length; j++) {
if (items[j] < items[minIdx]) {
minIdx = j;
}
}
let temp = items[i];
items[i] = items[minIdx];
items[minIdx] = temp;
}
return items;
}
let items = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53];
console.log(selectionSort(items));8. 基数排序
基数排序的基本思想是通过按被排序的数字或字符中的每个数字分组来对数据进行排序,从右到左或从左到右。对每个数字重复这个过程,得到一个排序列表。
其最坏情况性能为 O(w*cdotn),其中 n 为?key 数量,为 w 为键长度。
基数排序的历史
基数排序最早是由 Herman Hollerith 在 19 世纪末引入的,作为一种有效地对打孔卡片上的数据进行排序的方法,打孔卡片上的每一列代表数据中的一个数字。
后来,在 20 世纪中期,一些研究人员对它进行了改编和推广,通过按二进制表示中的每个比特对数据进行分组来对二进制数据进行排序。但它也用于对字符串数据进行排序,其中每个字符在排序中被视为数字。
近年来,基数排序作为并行和分布式计算环境的排序算法重新引起了人们的兴趣,因为它很容易并行化,并且可以用于以分布式方式对大型数据集进行排序。
 ?
?
一种 IBM 卡片分类器,对大量打孔卡片执行基数排序
基数排序的优点
基数排序是一种线性时间排序算法,这意味着它的时间复杂度与输入数据的大小成正比。这使得它成为对大型数据集进行排序的有效算法,尽管对于较小的数据集,它可能不如其他排序算法那么有效。
它的线性时间复杂度和稳定性使它成为对大型数据集排序的有用工具,它的并行性使它对分布式计算环境中的数据排序很有用。
基数排序也是一种稳定的排序算法,这意味着它保留相等元素的相对顺序。
基数排序的用处
基数排序可用于需要对大型数据集进行高效排序的各种应用程序。它对于排序字符串数据和固定长度的键特别有用,也可以用于并行和分布式计算环境。
并行处理:基数排序通常更适合于对大型数据集进行排序(优于归并排序、快速排序和桶排序)。像桶排序一样,基数可以有效地对字符串数据进行排序,这使得它适合于自然语言处理应用程序。
用固定长度的键排序数据:基数排序在对具有固定长度键的数据进行排序时特别有效,因为它可以通过每次检查每个键的一个数字来执行排序。
基数排序的实现
- 比较列表中每一项的数字。
- 按数字分组。
- 按大小对组进行排序。
- 递归地对每个组进行排序,直到每个项都在正确的位置。
Python 基数排序代码示例
def radix_sort(items):
max_length = False
tmp, placement = -1, 1
while not max_length:
max_length = True
buckets = [list() for _ in range(10)]
for i in items:
tmp = i // placement
buckets[tmp % 10].append(i)
if max_length and tmp > 0:
max_length = False
a = 0
for b in range(10):
buck = buckets[b]
for i in buck:
items[a] = i
a += 1
placement *= 10
return items
items = [6,20,8,19,56,23,87,41,49,53]
print(radix_sort(items))Javascript 基数排序代码示例
function radixSort(items) {
let maxLength = false;
let tmp = -1;
let placement = 1;
while (!maxLength) {
maxLength = true;
let buckets = Array.from({ length: 10 }, () => []);
for (let i = 0; i < items.length; i++) {
tmp = Math.floor(items[i] / placement);
buckets[tmp % 10].push(items[i]);
if (maxLength && tmp > 0) {
maxLength = false;
}
}
let a = 0;
for (let b = 0; b < 10; b++) {
let buck = buckets[b];
for (let j = 0; j < buck.length; j++) {
items[a] = buck[j];
a++;
}
}
placement *= 10;
}
return items;
}
let items = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53];
console.log(radixSort(items));9. 梳子排序
梳子排序比较相隔一定距离的元素对,如果它们顺序不一致,就交换它们。对之间的距离最初设置为正在排序的列表的大小,然后在每次传递时减少一个因子(称为“收缩因子”),直到达到最小值 1。重复这个过程,直到列表被完全排序。
梳子排序算法类似于冒泡排序算法,但比较元素之间的间隙更大。这个较大的间隙允许较大的值更快地移动到列表中的正确位置。
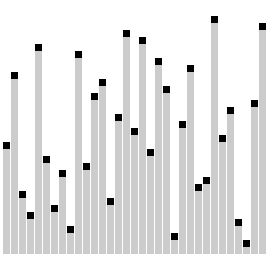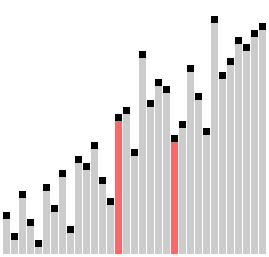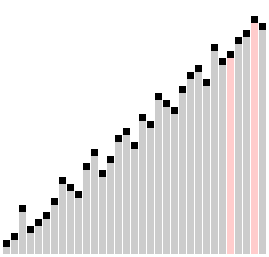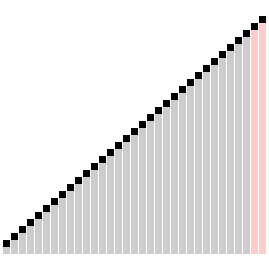 ?
?
梳子排序的历史
梳状排序算法是一种相对较新的排序算法,于 1980 年由 W?odzimierz Dobosiewicz 和Artur Borowy 首次提出。该算法的灵感来自于使用梳子理顺纠结的头发的想法,它使用类似的过程来理顺未排序的值列表。
梳子排序的优点
梳子排序的最坏情况时间复杂度为 O(n^2),但在实践中它通常比其他排序算法(如冒泡排序)快,因为它使用了收缩因子。收缩因子允许算法快速将大值移动到正确的位置,减少完全排序列表所需的传递次数。
梳子排序的用处
梳子排序是一种相对简单和有效的排序算法,在各种应用程序中:
- 排序具有大范围值的数据:在比较元素之间使用更大的间距可以让更大的值更快地移动到列表中的正确位置。
- 在实时应用程序中排序数据:梳子排序是一种稳定的排序算法,它保持了相等元素的相对顺序。这对于需要保留相等元素的顺序的实时应用程序中的数据排序非常有用。
- 在内存受限的环境中排序数据:梳子排序不需要额外的内存来对数据进行排序。这对于在内存受限的环境中对数据进行排序非常有用,因为在这种环境中没有额外的内存可用。
梳子排序的实现
- 从列表之间最大长度开始。
- 比较间隔末端的项,如果顺序不对就交换它们。
- 减小间隙并重复此过程,直到间隙为 1
- 最后对剩下的项进行冒泡排序。
Python 梳子排序代码示例
def comb_sort(items):
gap = len(items)
shrink = 1.3
sorted = False
while not sorted:
gap //= shrink
if gap <= 1:
sorted = True
else:
for i in range(len(items)-gap):
if items[i] > items[i+gap]:
items[i],items[i+gap] = items[i+gap],items[i]
return bubble_sort(items)
def bubble_sort(items):
for i in range(len(items)):
for j in range(len(items)-1-i):
if items[j] > items[j+1]:
items[j], items[j+1] = items[j+1], items[j]
return items
items = [6,20,8,19,56,23,87,41,49,53]
print(comb_sort(items))Javascript 梳子排序代码示例
function combSort(items) {
let gap = items.length;
let shrink = 1.3;
let sorted = false;
while (!sorted) {
gap = Math.floor(gap / shrink);
if (gap <= 1) {
sorted = true;
} else {
for (let i = 0; i < items.length - gap; i++) {
if (items[i] > items[i + gap]) {
let temp = items[i];
items[i] = items[i + gap];
items[i + gap] = temp;
}
}
}
}
return bubbleSort(items);
}
function bubbleSort(items) {
let swapped;
do {
swapped = false;
for (let i = 0; i < items.length - 1; i++) {
if (items[i] > items[i + 1]) {
let temp = items[i];
items[i] = items[i + 1];
items[i + 1] = temp;
swapped = true;
}
}
} while (swapped);
return items;
}
let items = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53];
console.log(combSort(items));10. Timsort
Timsort 算法的工作原理是将输入数据分成更小的子数组,然后使用插入排序对这些子数组进行排序。然后使用归并排序将这些排序的子数组组合起来,以产生一个完全排序的数组。
Timsort的最坏情况时间复杂度为 O(nlogn),这使得它对大型数据集的排序效率很高。它也是一种稳定的排序算法,这意味着它保留了相等元素的相对顺序。
Timsort 的历史
Timsort 是由 Tim Peters 在2002年为 Python 编程语言开发的。它是一种混合排序算法,结合使用插入排序和归并排序技术,旨在有效地对各种不同类型的数据进行排序。
由于它在处理不同类型数据方面的效率和通用性,它已经被其他几种编程语言所采用,包括Java和c#。
Timsort 的优点
Timsort 的一个关键特性是它能够有效地处理不同类型的数据。它通过检测“runs”来实现这一点,“runs”是已经排序的元素序列。Timsort 然后以一种最小化生成完全排序数组所需的比较和交换次数的方式组合这些运行。
Timsort 的另一个重要特性是它能够处理部分排序的数据。在这种情况下,Timsort 可以检测部分排序的区域,并使用插入排序对其进行快速排序,从而减少对数据进行完全排序所需的时间。
Timsort 的用处
作为一种高级算法,Timsort 可以用于在内存受限的系统上对数据进行排序。
编程语言中的排序:Timsort 通常被用作这些语言中的默认排序算法,因为它具有处理不同类型数据的效率和能力。
整理数据:Timsort 在对可能部分排序或包含已经排序的子数组的实际数据进行排序时特别高效,因为它能够检测这些运行并使用插入排序对它们进行快速排序,从而减少对数据进行完全排序所需的时间。
对不同类型的数据进行排序:它旨在有效地处理不同类型的数据,包括数字、字符串和自定义对象。它可以检测具有相同类型的数据运行,并使用归并排序有效地组合它们,减少所需的比较和交换次数。
Timsort 的实现
- 将一个未排序的列表分解成更小的、排序的子列表。
- 合并子列表以形成更大的排序列表。
- 重复这个过程,直到整个列表排序完毕。
Python Timsort代码示例
def insertion_sort(arr, left=0, right=None):
if right is None:
right = len(arr) - 1
for i in range(left + 1, right + 1):
key_item = arr[i]
j = i - 1
while j >= left and arr[j] > key_item:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key_item
return arr
def merge(left, right):
if not left:
return right
if not right:
return left
if left[0] < right[0]:
return [left[0]] + merge(left[1:], right)
return [right[0]] + merge(left, right[1:])
def timsort(arr):
min_run = 32
n = len(arr)
for i in range(0, n, min_run):
insertion_sort(arr, i, min((i + min_run - 1), n - 1))
size = min_run
while size < n:
for start in range(0, n, size * 2):
midpoint = start + size - 1
end = min((start + size * 2 - 1), (n-1))
merged_array = merge(
left=arr[start:midpoint + 1],
right=arr[midpoint + 1:end + 1]
)
arr[start:start + len(merged_array)] = merged_array
size *= 2
return arr
items = [6,20,8,19,56,23,87,41,49,53]
print(timsort(items))Javascript Timsort代码示例
function insertionSort(arr, left = 0, right = arr.length - 1) {
for (let i = left + 1; i <= right; i++) {
const keyItem = arr[i];
let j = i - 1;
while (j >= left && arr[j] > keyItem) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = keyItem;
}
return arr;
}
function merge(left, right) {
let i = 0;
let j = 0;
const merged = [];
while (i < left.length && j < right.length) {
if (left[i] < right[j]) {
merged.push(left[i]);
i++;
} else {
merged.push(right[j]);
j++;
}
}
return merged.concat(left.slice(i)).concat(right.slice(j));
}
function timsort(arr) {
const minRun = 32;
const n = arr.length;
for (let i = 0; i < n; i += minRun) {
insertionSort(arr, i, Math.min(i + minRun - 1, n - 1));
}
let size = minRun;
while (size < n) {
for (let start = 0; start < n; start += size * 2) {
const midpoint = start + size - 1;
const end = Math.min(start + size * 2 - 1, n - 1);
const merged = merge(
arr.slice(start, midpoint + 1),
arr.slice(midpoint + 1, end + 1)
);
arr.splice(start, merged.length, ...merged);
}
size *= 2;
}
return arr;
}
let items = [6, 20, 8, 19, 56, 23, 87, 41, 49, 53];
console.log(timsort(items));比较所有排序算法
请注意,表中列出的时间复杂度和空间复杂度是最坏情况复杂度,实际性能可能因具体实现和输入数据而异。
| 算法 | 时间复杂度 | 空间复杂性 | 就地排序 | 是否稳定 | 自适应排序 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(1) | 是 | 是 | 否 |
| 快速排序 | O(nlogn) | O(logn) | 是 | 否 | 是 |
| 桶排序 | O(n+k) | O(n+k) | 不 | 是 | 否 |
| Shell 排序 | O(nlogn) | $O(1) | 是 | 否 | 否 |
| 归并排序 | $O(n \log n)$ | O(n) | 否 | 是 | 否 |
| 选择排序 | $O(n^2)$ | O(1) | 是 | 否 | 否 |
| 基数排序 | O(w*cdotn) | O(w+n) | 否 | 是 | 否 |
| 梳子排序 | O(n^2) | O(1) | 是 | 否 | 是 |
| Timsort | O(nlogn) | O(n) | 是 | 是 | 是 |
最常见的排序算法是什么?
最常用的排序算法可能是快速排序。它广泛用于许多编程语言,包括 C、C++、Java 和 Python,以及许多软件应用程序和库。快速排序因其在处理不同类型数据方面的效率和多功能性而受到青睐,并且经常被用作编程语言和软件框架中的默认排序算法。
然而,其他排序算法,如?归并排序 和?Timsort,由于其效率和独特的功能,也常用于各种应用程序。
写在最后
对于任何对编程、数据分析或计算机科学感兴趣的人来说,了解排序算法的基础知识都是必不可少的。通过了解不同的排序算法及其特征,您可以提高为特定用例选择和实施最佳算法的能力。
排序算法的最佳选择取决于几个因素,包括输入数据的大小、数据的分布、可用内存和所需的时间复杂度。
排序算法可以根据其时间复杂度、空间复杂度、就地排序、稳定排序和自适应排序进行分类。了解不同排序算法的特征和权衡对于为特定用例选择最合适的算法非常重要。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- UWB及其相关概念扫盲
- “镇好采”服务类网上商城是什么
- 产品经理必备之最强管理项目过程工具----禅道
- swin transformer的SW-MSA中的masked理解
- 05 Ciso模拟器连接腾讯云物联网开发平台
- geemap学习笔记048:光谱变换
- signaltap立即触发的错误解决方法
- 邦芒攻略:职场高效沟通的8个说话小技巧
- 轻松掌握构建工具:Webpack、Gulp、Grunt 和 Rollup 的使用技巧(下)
- 前后端分离下的鸿鹄电子招投标系统:使用Spring Boot、Mybatis、Redis和Layui实现源码与立项流程