【数据结构入门精讲 | 第六篇】队列知识点及考研408、企业面试练习

在上一篇文章中我们介绍了栈的知识点及相关练习，在这一篇文章中我们将介绍队列的知识点并通过练习来巩固。

队列

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。队列中没有元素时，称为空队列。

队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队，从队列中删除一个队列元素称为出队。因为队列只允许在一端插入，在另一端删除，所以只有最早进入队列的元素才能最先从队列中删除，故队列又称为先进先出（FIFO—first in first out）线性表。

队列的数组实现

基础概念

队列是一种先进先出（FIFO）的数据结构，它可以用数组来实现。在队列的数组实现中，使用一个固定大小的数组作为存储容器，在队列的操作过程中，通过维护队头和队尾的指针来实现元素的入队和出队。

伪代码

QueueArrayInit(queueSize)
    queue = new Array[queueSize]  // 创建一个大小为queueSize的数组
    front = -1  // 队列前端指针初始化为-1
    rear = -1  // 队列后端指针初始化为-1
    return queue


QueueArrayIsEmpty(queue)
    if front = -1 and rear = -1 then
        return true  // 如果前端指针和后端指针都为-1，则队列为空
    else
        return false // 否则队列不为空


QueueArrayIsFull(queue, queueSize)
    if rear = queueSize-1 then
        return true  // 如果后端指针指向了最后一个元素，则队列已满
    else
        return false // 否则队列未满


QueueArrayEnqueue(queue, queueSize, item)
    if QueueArrayIsFull(queue, queueSize) then
        return "Queue is full"  // 如果队列已满，则无法入队
    else if QueueArrayIsEmpty(queue) then
        front = 0  // 如果队列为空，则将前端指针移到第一个位置
    end if
    rear = rear + 1  // 后端指针后移一位
    queue[rear] = item  // 将元素存入队列中


QueueArrayDequeue(queue)
    if QueueArrayIsEmpty(queue) then
        return "Queue is empty"  // 如果队列为空，则无法出队
    else if front = rear then
        front = -1  // 如果队列只有一个元素，则将前端指针和后端指针重置为-1
        rear = -1
    else
        front = front + 1  // 前端指针后移一位
    end if
    return queue[front]  // 返回出队的元素

队列的循环数组实现

基础概念

队列的循环数组实现是对队列的数组实现的一种改进。通过使用循环数组，可以充分利用数组空间，避免浪费。当队尾指针到达数组末尾时，如果队头指针不在数组开头，可以将队尾指针循环回到数组开头，实现循环利用。

伪代码

QueueCircularInit(queueSize)
    queue = new Array[queueSize]  // 创建一个大小为queueSize的数组
    front = -1  // 初始化前端指针为-1
    rear = -1   // 初始化后端指针为-1


QueueCircularIsEmpty()
    if front = -1 and rear = -1 then
        return true  // 如果前端指针和后端指针都为-1，则队列为空
    else
        return false // 否则队列不为空


QueueCircularIsFull()
    if (rear + 1) % queueSize = front then
        return true  // 如果后端指针加1后取模等于前端指针，则队列已满
    else
        return false // 否则队列未满




QueueCircularEnqueue(item)
    if QueueCircularIsFull() then
        return "Queue is full"  // 如果队列已满，则无法入队
    else if QueueCircularIsEmpty() then
        front = 0  // 如果队列为空，则将前端指针设置为0
    end if
    rear = (rear + 1) % queueSize  // 后端指针后移一位，并取模queueSize
    queue[rear] = item  // 将元素放入队列的后端位置




QueueCircularDequeue()
    if QueueCircularIsEmpty() then
        return "Queue is empty"  // 如果队列为空，则无法出队
    else if front = rear then
        front = -1  // 如果队列中只有一个元素，则出队后将前端指针重置为-1
        rear = -1   // 同时将后端指针也重置为-1
    else
        front = (front + 1) % queueSize  // 前端指针后移一位，并取模queueSize
    end if
    item = queue[front]  // 获取出队的元素
    return item

队列的链表实现

基础概念

队列的链表实现使用链表作为存储结构，在队列的操作过程中，通过维护队头和队尾节点的指针来实现元素的入队和出队。

伪代码

以下是队列的链表实现的伪代码：

QueueLinkedListInit()
    head = null  // 将队列的头指针指向空，表示队列为空
    tail = null  // 将队列的尾指针指向空，表示队列为空


QueueLinkedListIsEmpty()
    return head == null  // 如果头指针为null，则队列为空，返回true；否则返回false




QueueLinkedListEnqueue(item)
    newNode = new Node(item)  // 创建一个新的结点，存储待入队的元素
    if QueueLinkedListIsEmpty() then
        head = newNode   // 如果队列为空，则将头指针和尾指针都指向新结点
        tail = newNode
    else
        tail.next = newNode  // 否则，将新结点添加到尾结点的后面，并将尾指针指向新结点
        tail = newNode


QueueLinkedListDequeue()
    if QueueLinkedListIsEmpty() then
        return "Queue is empty"  // 如果队列为空，则无法出队
    else
        item = head.item  // 获取头结点的元素
        head = head.next   // 将头指针指向下一个结点
        if head == null then
            tail = null   // 如果队列中只有一个元素，则出队后将尾指针也置为null
        end if
        return item

接下来让我们进行队列的相关练习

判断题

循环数组实现队列时，当front和rear满足什么关系时队列为空？front==rear

满足什么关系时队列为满？(rear+1)%m=front

1.所谓“循环队列”是指用单向循环链表或者循环数组表示的队列。（错）

解析：循环队列指的是用数组表示的队列，利用求余数运算使得头尾相接。循环队列本身是一种顺序存储结构，而循环链表是一种链式存储结构。

2.队列适合解决处理顺序与输入顺序相反的问题。（错）

解析：栈是后进先出的，可以很方便地处理与输入顺序相反的情况。

3.不论是入队列操作还是入栈操作,在顺序存储结构上都需要考虑"溢出"情况。 （对）

解析：对于队列，当队列已满时，再进行入队操作就会发生溢出，称为队列满的情况。对于栈，当栈已满时，再进行入栈操作就会发生溢出，称为栈满的情况。

4.循环队列也存在空间溢出的问题。（对）

5.所谓“循环队列”是指用单向循环链表或者循环数组表示的队列。（错）

解析：循环队列是数组实现的。

选择题

1.已知初始为空的队列 Q 的一端仅能进行入队操作，另外一端既能进行入队操作又能进行出队操作。若 Q 的入队序列是 1、2、3、4、5，则不能得到的出队序列是：

A.4、1、3、2、5

B.4、2、1、3、5

C.5、4、3、1、2

D.5、3、1、2、4

选A，解析：对于A，并不能找到一个数字，使之左边是递减序列、右边是递增序列。

对于B，1、3、5右边入，2、4左边入，从左边开始出队操作。

对于C，1、2右边入，3、4、5左边入，从左边开始出队操作。

对于D，1、2、4右边入，3、5左边入，从右边开始出队操作。

2.在一个不带头结点的非空链式队列中,假设f和r分别为队头和队尾指针,则插入s所指的结点运算是( )。

A.s->next=s; r=s;

B.s->next=f; f=s;

C.r->next=s; r=s;

D.f->next=s; f=s;

选C，解析：链式队列在队尾进行插入。

3.循环队列的引入，目的是为了克服( 假溢出问题 )。

解析：假溢出问题是指当队列头部指针追上队列尾部指针时，即使队列中仍有空闲位置，队列也会被错误地判断为满，导致无法继续入队操作。通过循环队列的设计，可以有效地避免这种情况，使得队列能够循环利用数组空间，提高了队列的存储效率。

4.如果循环队列用大小为m的数组表示，且用队头指针front和队列元素个数size代替一般循环队列中的front和rear指针来表示队列的范围，那么这样的循环队列可以容纳的元素个数最多为：（m）

解析：在这种实现方式下，队列满的条件是(front + size) % m == front，即队列中的元素个数等于数组的大小。

5.若已知一队列用单向链表表示，该单向链表的当前状态（含3个对象）是：1->2->3，其中x->y表示x的下一节点是y。此时，如果将对象4入队，然后队列头的对象出队，则单向链表的状态是：

A.

1->2->3

B.

2->3->4

C.

4->1->2

D.

答案不唯一

选B，解析：4入队之后3指向4，同时1出队。

6.线性表、堆栈、队列的主要区别是什么？

A.堆栈和队列都不是线性结构，而线性表是

B.线性表和队列都可以用循环链表实现，但堆栈不能

C.堆栈和队列都是插入、删除受到约束的线性表，因为一个新元素的插入只能在特定的地方。

D.线性表用指针，堆栈和队列用数组

选C，解析：对于A，栈堆、队列、线性表都是线性结构。对于B，三者都能用循环链表实现。C对。对于D，三者都能用链表实现。

7.最不适合用作链队的链表是（）。

A.只带队尾指针的循环单链表

B.只带队头指针的非循环双链表

C.只带队尾指针的循环双链表

D.只带队头指针的循环双链表

选B，解析：B项查找队尾时间复杂度最长为O（n）,其他都只需要O（1）

8.循环顺序队列中是否可以插入下一个元素（）。

A.与曾经进行过多少次插入操作有关

B.只与队尾指针的值有关，与队头指针的值无关

C.只与数组大小有关，与队首指针和队尾指针的值无关

D.与队头指针和队尾指针的值有关

选D，解析：是否可以插入下一个元素需要判断是否front==(rear+1)%n

9.循环队列存储在数组A[0,m]中，则入队时的部分操作为__C__。
A.rear=rear+1
B.rear=(rear+1)mod(m-1)
C.rear=(rear+1)mod(m+1)
D.rear=(rear+1)mod m

10.写出下列程序段的输出结果（队列中的元素类型QElem Type为char）。

void main(){
Queue Q;Init Queue(Q);
Char x=’e’;y=’c’;
EnQueue(Q,’h’);EnQueue(Q,’r’);EnQueue(Q,y);
DeQueue(Q,x);EnQueue(Q,x);
DeQueue(Q,x);EnQueue(Q,’a’);
While(!QueueEmpty(Q))
{DeQueue(Q,y);
Printf(y);
};
Printf(x);
}

首先，初始化一个空队列Q。
将字符'h'、'r'和变量y的值（'c'）依次入队。
执行DeQueue(Q, x)，将队头元素赋值给变量x，即将'h'出队。
执行EnQueue(Q, x)，将变量x的值（'h'）入队。
再次执行DeQueue(Q, x)，将队头元素赋值给变量x，即将'r'出队。
执行EnQueue(Q, 'a')，将字符'a'入队。
进入循环，依次执行DeQueue(Q, y)并输出y的值。
最后，输出变量x的值。
所以是char

设指针变量front表示链式队列的队头指针，指针变量rear表示链式队列的队尾指针，指针变量s指向将要入队列的结点X，则入队列的操作序列为（ B ）。

A. front->next=s；front=s； B. s->next=rear；rear=s；

C. rear->next=s；rear=s； D. s->next=front；front=s；

进行图的广度优先搜索时，需要用到下列哪种数据结构（队列）。

函数题

R6-1 双端队列

双端队列（deque，即double-ended queue的缩写）是一种具有队列和栈性质的数据结构，即可以（也只能）在线性表的两端进行插入和删除。若以顺序存储方式实现双端队列，请编写例程实现下列操作：

• Push(X,D)：将元素X插入到双端队列D的头；
• Pop(D)：删除双端队列D的头元素，并返回；
• Inject(X,D)：将元素X插入到双端队列D的尾部；
• Eject(D)：删除双端队列D的尾部元素，并返回。

函数接口定义：

bool Push( ElementType X, Deque D );
ElementType Pop( Deque D );
bool Inject( ElementType X, Deque D );
ElementType Eject( Deque D );

其中Deque结构定义如下：

typedef int Position;
typedef struct QNode *PtrToQNode;
struct QNode {
    ElementType *Data;      /* 存储元素的数组   */
    Position Front, Rear;   /* 队列的头、尾指针 */
    int MaxSize;            /* 队列最大容量     */
};
typedef PtrToQNode Deque; 

注意：Push和Inject应该在正常执行完操作后返回true，或者在出现非正常情况时返回false。当Front和Rear相等时队列为空，Pop和Eject必须返回由裁判程序定义的ERROR。

裁判测试程序样例：

#include <stdio.h>
#include <stdlib.h>

#define ERROR -1
typedef int ElementType;
typedef enum { push, pop, inject, eject, end } Operation;
typedef enum { false, true } bool;
typedef int Position;
typedef struct QNode *PtrToQNode;
struct QNode {
    ElementType *Data;      /* 存储元素的数组   */
    Position Front, Rear;   /* 队列的头、尾指针 */
    int MaxSize;            /* 队列最大容量     */
};
typedef PtrToQNode Deque; 

Deque CreateDeque( int MaxSize )
{   /* 注意：为区分空队列和满队列，需要多开辟一个空间 */
    Deque D = (Deque)malloc(sizeof(struct QNode));
    MaxSize++;
    D->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
    D->Front = D->Rear = 0;
    D->MaxSize = MaxSize;
    return D;
}

bool Push( ElementType X, Deque D );
ElementType Pop( Deque D );
bool Inject( ElementType X, Deque D );
ElementType Eject( Deque D );

Operation GetOp();          /* 裁判实现，细节不表 */
void PrintDeque( Deque D ); /* 裁判实现，细节不表 */

int main()
{
    ElementType X;
    Deque D;
    int N, done = 0;

    scanf("%d", &N);
    D = CreateDeque(N);
    while (!done) {
        switch(GetOp()) {
        case push: 
            scanf("%d", &X);
            if (!Push(X, D)) printf("Deque is Full!\n");
            break;
        case pop:
            X = Pop(D);
            if ( X==ERROR ) printf("Deque is Empty!\n");
            else printf("%d is out\n", X);
            break;
        case inject: 
            scanf("%d", &X);
            if (!Inject(X, D)) printf("Deque is Full!\n");
            break;
        case eject:
            X = Eject(D);
            if ( X==ERROR ) printf("Deque is Empty!\n");
            else printf("%d is out\n", X);
            break;
        case end:
            PrintDeque(D);
            done = 1;
            break;
        }
    }
    return 0;
}

/* 你的代码将被嵌在这里 */

输入样例：

3
Pop
Inject 1
Pop
Eject
Push 2
Push 3
Eject
Inject 4
Inject 5
Inject 6
Push 7
Pop
End

输出样例：

Deque is Empty!
1 is out
Deque is Empty!
2 is out
Deque is Full!
Deque is Full!
3 is out
Inside Deque: 4 5

bool Push( ElementType X, Deque D )
{
    if((D->Rear+1)%D->MaxSize==D->Front)
        return false;
    D->Front=(D->Front-1+D->MaxSize)%D->MaxSize;
    D->Data[D->Front]=X;
    return true;
}
ElementType Pop( Deque D )
{
    if(D->Rear==D->Front)
        return ERROR;
     int x=D->Data[D->Front];
     D->Front=(D->Front+1)%D->MaxSize;
     return x;
}
bool Inject( ElementType X, Deque D )
{
    if((D->Rear+1)%D->MaxSize==D->Front)
        return false;
    D->Data[D->Rear]=X;
    D->Rear=(D->Rear+1)%D->MaxSize;
    return true;
}
ElementType Eject( Deque D )
{
    if(D->Rear==D->Front)
        return ERROR;
    D->Rear=(D->Rear-1+D->MaxSize)%D->MaxSize;
    return D->Data[D->Rear];
}

编程题

R7-1 列车调度

火车站的列车调度铁轨的结构如下图所示。

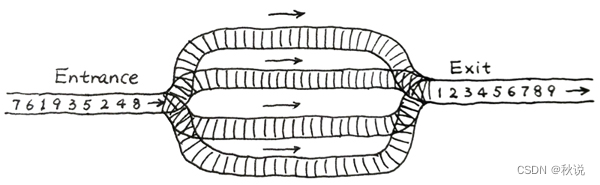
两端分别是一条入口（Entrance）轨道和一条出口（Exit）轨道，它们之间有N条平行的轨道。每趟列车从入口可以选择任意一条轨道进入，最后从出口离开。在图中有9趟列车，在入口处按照{8，4，2，5，3，9，1，6，7}的顺序排队等待进入。如果要求它们必须按序号递减的顺序从出口离开，则至少需要多少条平行铁轨用于调度？

输入格式：

输入第一行给出一个整数N (2 ≤ N ≤105)，下一行给出从1到N的整数序号的一个重排列。数字间以空格分隔。

输出格式：

在一行中输出可以将输入的列车按序号递减的顺序调离所需要的最少的铁轨条数。

输入样例：

9
8 4 2 5 3 9 1 6 7

输出样例：

4

#include <stdio.h>
int main()
{
	int n;scanf("%d",&n);
	int a[n],len=0;//存储递增子序列的数组、当前最长递增子序列的长度
	for(int i=0;i<n;i++)
	{
		int k;scanf("%d",&k);
		if(len==0||a[len-1]<k)
//如果当前最长递增子序列为空，或者当前数字大于最长递增子序列的尾部元素
//将当前数字添加到最长递增子序列的末尾，并更新最长子序列的长度
        {
		a[len]=k;
		len++;
	    }
		else
//使用二分搜索找到合适的位置插入当前数字，以保持子序列的递增性质
		{
			int l=0,r=len-1;
			while(l<r)
			{
				int mid=l+(r-l)/2;
				if(a[mid]>k)
				{
					r=mid-1;
				}
				else
				{
					l=mid+1;
				}
			}
			a[l]=k;
		}        
	}
	printf("%d",len);
}

R7-1 银行排队问题之单窗口“夹塞”版

排队“夹塞”是引起大家强烈不满的行为，但是这种现象时常存在。在银行的单窗口排队问题中，假设银行只有1个窗口提供服务，所有顾客按到达时间排成一条长龙。当窗口空闲时，下一位顾客即去该窗口处理事务。此时如果已知第i位顾客与排在后面的第j位顾客是好朋友，并且愿意替朋友办理事务的话，那么第i位顾客的事务处理时间就是自己的事务加朋友的事务所耗时间的总和。在这种情况下，顾客的等待时间就可能被影响。假设所有人到达银行时，若没有空窗口，都会请求排在最前面的朋友帮忙（包括正在窗口接受服务的朋友）；当有不止一位朋友请求某位顾客帮忙时，该顾客会根据自己朋友请求的顺序来依次处理事务。试编写程序模拟这种现象，并计算顾客的平均等待时间。

输入格式:

输入的第一行是两个整数：1≤N≤10000，为顾客总数；0≤M≤100，为彼此不相交的朋友圈子个数。若M非0，则此后M行，每行先给出正整数2≤L≤100，代表该圈子里朋友的总数，随后给出该朋友圈里的L位朋友的名字。名字由3个大写英文字母组成，名字间用1个空格分隔。最后N行给出N位顾客的姓名、到达时间T和事务处理时间P（以分钟为单位），之间用1个空格分隔。简单起见，这里假设顾客信息是按照到达时间先后顺序给出的（有并列时间的按照给出顺序排队），并且假设每个事务最多占用窗口服务60分钟（如果超过则按60分钟计算）。

输出格式:

按顾客接受服务的顺序输出顾客名字，每个名字占1行。最后一行输出所有顾客的平均等待时间，保留到小数点后1位。

输入样例:

6 2
3 ANN BOB JOE
2 JIM ZOE
JIM 0 20
BOB 0 15
ANN 0 30
AMY 0 2
ZOE 1 61
JOE 3 10

输出样例:

JIM
ZOE
BOB
ANN
JOE
AMY
75.2

#include <bits/stdc++.h>

using namespace std;
const int maxn=10000+10;

struct node
{
    string name;
    int arrive,work;
}que[maxn];

int main()
{
    int n,m;  // 顾客数量和好友圈子数量
    cin>>n>>m;

    // 存储好友关系
    vector<string> friends[maxn];
    // 存储每个人的编号
    map<string, int> number; 

    for(int i=1;i<=m;i++)
    {
        int num; 
        cin>>num;  // 好友圈子中的人数
        for(int j=0;j<num;j++)
        {
            string s; 
            cin>>s;  // 输入每个人的姓名
            number[s]=i;  // 将姓名作为键，将好友圈子的编号作为值存储到映射number中
            friends[i].push_back(s);  // 将每个人的姓名存储到对应的好友圈子中
        }
    }

    // 存储每个顾客的编号
    map<string,int> norder;

    for(int i=1;i<=n;i++)
    {
        string s; 
        int a,b; 
        cin>>s>>a>>b;  // 输入顾客的姓名、到达时间和需要处理的时间
        que[i].name=s,que[i].arrive=a,que[i].work= b>=60? 60 : b;  // 将顾客的信息存储到结构体que中
        norder[s]=i;  // 将顾客的姓名作为键，将顾客的编号作为值存储到映射norder中
    }

    // 存储好友圈子中每个人的编号，并按照编号从小到大进行排序
    vector<int>  reorder[maxn];
    for(int i=1;i<=m;i++)
    {
        for(int j=0;j<friends[i].size();j++)
        {
            int x=norder[friends[i][j]];  // 获取好友的编号
            reorder[i].push_back(x);  // 将好友的编号存储到对应的好友圈子中
        }

        sort(reorder[i].begin(),reorder[i].end());  // 对好友圈子中的编号进行排序
    }

    // 标记每个顾客是否已经被处理过
    bool vis[maxn]; 
    memset(vis,false,sizeof(vis));

    int time=0,ans=0;  // 当前时间和总等待时间

    for(int i=1;i<=n;i++)
    {
        if(vis[i]==true) continue;  // 如果顾客已经被处理过，则继续下一个顾客

        vis[i]=true;  // 将当前顾客标记为已处理

        cout<<que[i].name<<endl;  // 输出当前正在处理的顾客的姓名

        if(que[i].arrive>=time) 
            time=que[i].work+que[i].arrive;  // 如果顾客的到达时间在当前时间之后，则直接处理该顾客
        else
        {
            ans+=time-que[i].arrive;  // 如果顾客的到达时间在当前时间之前，则需要等待一段时间
            time+=que[i].work;  // 更新当前时间为顾客处理完毕的时间
        }

        int x=number[que[i].name];  // 获取当前顾客所在的好友圈子编号

        for(int j=0;j<reorder[x].size();j++)
        {
            int t=reorder[x][j];  // 获取当前好友圈子中的好友编号

            if(vis[t]==true) continue;  // 如果好友已经被处理过，则继续下一个好友

            if(que[t].arrive<=time)
            {
                vis[t]=true;  // 将好友标记为已处理
                ans+=time-que[t].arrive;  // 累加等待时间
                time+=que[t].work;  // 更新当前时间为好友处理完毕的时间
                cout<<que[t].name<<endl;  // 输出当前正在处理的好友的姓名
            }
        }
    }

    printf("%.1f",ans*1.0/n);  // 输出平均等待时间

    return 0;
}

R7-2 银行排队问题之单队列多窗口服务

假设银行有K个窗口提供服务，窗口前设一条黄线，所有顾客按到达时间在黄线后排成一条长龙。当有窗口空闲时，下一位顾客即去该窗口处理事务。当有多个窗口可选择时，假设顾客总是选择编号最小的窗口。

本题要求输出前来等待服务的N位顾客的平均等待时间、最长等待时间、最后完成时间，并且统计每个窗口服务了多少名顾客。

输入格式:

输入第1行给出正整数N（≤1000），为顾客总人数；随后N行，每行给出一位顾客的到达时间T和事务处理时间P，并且假设输入数据已经按到达时间先后排好了顺序；最后一行给出正整数K（≤10），为开设的营业窗口数。这里假设每位顾客事务被处理的最长时间为60分钟。

输出格式:

在第一行中输出平均等待时间（输出到小数点后1位）、最长等待时间、最后完成时间，之间用1个空格分隔，行末不能有多余空格。

在第二行中按编号递增顺序输出每个窗口服务了多少名顾客，数字之间用1个空格分隔，行末不能有多余空格。

输入样例：

9
0 20
1 15
1 61
2 10
10 5
10 3
30 18
31 25
31 2
3

输出样例：

6.2 17 61
5 3 1

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<vector>
#include<cstdlib>
using namespace std;
const int maxn = 105000;
int wintime[15] = {}; // 每个柜台的完成时间
struct Guest{
    int T; // 到达时间
    int P; // 处理时间
}temp[maxn];
struct window{
    int index; // 柜台编号
    int count; // 已处理顾客数量
}win[maxn];
struct compare{
    bool operator()(const int &x,const int &y) const {
        if(wintime[x] != wintime[y]) return wintime[x] > wintime[y]; // 按照完成时间升序排序
        return x > y; // 如果完成时间相同，按照柜台编号升序排序
    }
};
int main()
{
    int N,K;
    priority_queue<int,vector<int>,compare>Q; // 优先队列，按照compare中定义的规则排序
    cin>>N; // 输入顾客数量
    int endtime = 0,maxtime = 0,waittime = 0; // 结束时间、最长等待时间、总等待时间
    for(int i = 0;i < N;i++){
        cin>>temp[i].T; // 输入每个顾客的到达时间
        cin>>temp[i].P; // 输入每个顾客的处理时间
        if(temp[i].P > 60) temp[i].P = 60; // 如果处理时间超过60分钟，则限制为60分钟
    }
    cin>>K; // 输入柜台数量
    for(int i = 0;i < K;i++){
        win[i].index = i; // 初始化柜台编号
        win[i].count = 0; // 初始化已处理顾客数量
        Q.push(i); // 将柜台编号放入优先队列
    }
    for(int i = 0;i < N;i++){ // 处理每个顾客
        while(wintime[Q.top()] < temp[i].T){ // 更新柜台的完成时间，直到当前顾客的到达时间之前的柜台都完成了任务
            int ww = Q.top();
            Q.pop();
            wintime[ww] = temp[i].T; // 更新柜台的完成时间为当前顾客的到达时间
            Q.push(ww);
        }
        int ww = Q.top(); // 取出一个柜台
        Q.pop();
        win[ww].count++; // 已处理顾客数量增加
        if(wintime[ww] > temp[i].T){ // 如果柜台的完成时间大于当前顾客的到达时间，说明顾客需要等待
            waittime += wintime[ww] - temp[i].T; // 累加等待时间
            maxtime = max(maxtime,wintime[ww] - temp[i].T); // 更新最长等待时间
        }
        wintime[ww] = max(wintime[ww],temp[i].T) + temp[i].P; // 更新柜台的完成时间
        endtime = max(endtime,wintime[ww]); // 更新结束时间
        Q.push(ww); // 将柜台放回优先队列
    }
    printf("%.1f %d %d\n",waittime*1.0/N,maxtime,endtime); // 输出平均等待时间、最长等待时间和所有顾客完成业务的时间
    for(int i = 0;i < K;i++){
        if(i) printf(" ");
        cout<<win[i].count; // 输出每个柜台已处理的顾客数量
    }
    printf("\n");
    return 0;
}

R7-3 银行排队问题之单队列多窗口加VIP服务

假设银行有K个窗口提供服务，窗口前设一条黄线，所有顾客按到达时间在黄线后排成一条长龙。当有窗口空闲时，下一位顾客即去该窗口处理事务。当有多个窗口可选择时，假设顾客总是选择编号最小的窗口。

有些银行会给VIP客户以各种优惠服务，例如专门开辟VIP窗口。为了最大限度地利用资源，VIP窗口的服务机制定义为：当队列中没有VIP客户时，该窗口为普通顾客服务；当该窗口空闲并且队列中有VIP客户在等待时，排在最前面的VIP客户享受该窗口的服务。同时，当轮到某VIP客户出列时，若VIP窗口非空，该客户可以选择空闲的普通窗口；否则一定选择VIP窗口。

本题要求输出前来等待服务的N位顾客的平均等待时间、最长等待时间、最后完成时间，并且统计每个窗口服务了多少名顾客。

输入格式:

输入第1行给出正整数N（≤1000），为顾客总人数；随后N行，每行给出一位顾客的到达时间T、事务处理时间P和是否VIP的标志（1是VIP，0则不是），并且假设输入数据已经按到达时间先后排好了顺序；最后一行给出正整数K（≤10）—— 为开设的营业窗口数，以及VIP窗口的编号（从0到K?1）。这里假设每位顾客事务被处理的最长时间为60分钟。

输出格式:

在第一行中输出平均等待时间（输出到小数点后1位）、最长等待时间、最后完成时间，之间用1个空格分隔，行末不能有多余空格。

在第二行中按编号递增顺序输出每个窗口服务了多少名顾客，数字之间用1个空格分隔，行末不能有多余空格。

输入样例：

10
0 20 0
0 20 0
1 68 1
1 12 1
2 15 0
2 10 0
3 15 1
10 12 1
30 15 0
62 5 1
3 1

输出样例：

15.1 35 67
4 5 1

#include<iostream>
#include<cstdio>
#include<string>
#include<queue>

using namespace std;

int peo[1100][4]; // 存放顾客信息的二维数组，每一行包含到达时间、服务时间、等待时间和是否为VIP的信息
int num[20]; // 记录各个窗口完成的顾客数量
int ck[20]; // 记录各个窗口的完成时间
int ckm; // 记录当前正在工作的窗口
int dqtime; // 当前时间

int main(){
	int n, k, vip;
	int dd_max = 0, dd_sum = 0, timesum = 0;
	int t = 0;
	
	// 输入顾客信息
	scanf("%d",&n);
	for(int i=0; i<n; i++){
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		peo[i][0] = a; peo[i][3] = c;
		if( b <= 60 ) peo[i][1] = b;
		else peo[i][1] = 60;
	}
	
	// 输入窗口数量和VIP窗口编号
	int p = 0;
	scanf("%d%d",&k,&vip);
	
	// 模拟每一秒钟的排队处理过程
	for(dqtime = 0; p<n; dqtime++){
		// 更新各个窗口的完成情况
		if( dqtime != 0 )
			for( int i=0; i<k; i++)
				if(ck[i] == dqtime) ckm--;
		
		// VIP服务
		int vip_x = 0, flag = 0;
		for(  ; ckm<k && p+vip_x<n && peo[p+vip_x][0] <= dqtime ; vip_x++ )
			if(peo[p+vip_x][3] == 1) {
				flag = 1 ; break;
			}
		if( flag && ck[vip] <= dqtime){
			num[vip]++; ckm++;
			ck[vip] = dqtime+peo[p+vip_x][1];
			peo[p+vip_x][2] = dqtime-peo[p+vip_x][0];
			peo[p+vip_x][3] = 2;
		}
		
		// 正常服务
		while( ckm<k && p<n && peo[p][0]<=dqtime ){
			while( p<n && peo[p][0]<=dqtime) {
				if(peo[p][3] == 2) p++;
				else break;
			}
			if( p>=n || peo[p][0]>dqtime ) break;
			for( int i=0; i<k; i++ ){
				if(ck[i] <= dqtime){
					num[i]++;   ckm++;
					ck[i] = dqtime+peo[p][1];
					peo[p][2] = dqtime-peo[p][0];
					p++;
					break;
				}
			} 
		}
		if(p >= n)break;	
	} 
	
	// 计算平均等待时间、最长等待时间和所有窗口的完成时间
	for(int i=0; i<k; i++)
		if(  ck[i] >= timesum) timesum = ck[i];
	for(int i=0; i<n; i++){
		dd_sum += peo[i][2];
		if( peo[i][2] >= dd_max) dd_max = peo[i][2];
	}
	double ave = dd_sum*1.0/n;
	
	// 输出结果
	printf("%.1lf %d %d\n",ave,dd_max,timesum);
	for(int i=0; i<k; i++){
		if( i ) printf(" ");
		printf("%d",num[i]);
	}
	
	return 0;
}

R7-4 插松枝

人造松枝加工场的工人需要将各种尺寸的塑料松针插到松枝干上，做成大大小小的松枝。他们的工作流程（并不）是这样的：

• 每人手边有一只小盒子，初始状态为空。
• 每人面前有用不完的松枝干和一个推送器，每次推送一片随机型号的松针片。
• 工人首先捡起一根空的松枝干，从小盒子里摸出最上面的一片松针 —— 如果小盒子是空的，就从推送器上取一片松针。将这片松针插到枝干的最下面。
• 工人在插后面的松针时，需要保证，每一步插到一根非空松枝干上的松针片，不能比前一步插上的松针片大。如果小盒子中最上面的松针满足要求，就取之插好；否则去推送器上取一片。如果推送器上拿到的仍然不满足要求，就把拿到的这片堆放到小盒子里，继续去推送器上取下一片。注意这里假设小盒子里的松针片是按放入的顺序堆叠起来的，工人每次只能取出最上面（即最后放入）的一片。
• 当下列三种情况之一发生时，工人会结束手里的松枝制作，开始做下一个：

（1）小盒子已经满了，但推送器上取到的松针仍然不满足要求。此时将手中的松枝放到成品篮里，推送器上取到的松针压回推送器，开始下一根松枝的制作。

（2）小盒子中最上面的松针不满足要求，但推送器上已经没有松针了。此时将手中的松枝放到成品篮里，开始下一根松枝的制作。

（3）手中的松枝干上已经插满了松针，将之放到成品篮里，开始下一根松枝的制作。

现在给定推送器上顺序传过来的 N 片松针的大小，以及小盒子和松枝的容量，请你编写程序自动列出每根成品松枝的信息。

输入格式：

输入在第一行中给出 3 个正整数：N（≤103），为推送器上松针片的数量；M（≤20）为小盒子能存放的松针片的最大数量；K（≤5）为一根松枝干上能插的松针片的最大数量。

随后一行给出 N 个不超过 100 的正整数，为推送器上顺序推出的松针片的大小。

输出格式：

每支松枝成品的信息占一行，顺序给出自底向上每片松针的大小。数字间以 1 个空格分隔，行首尾不得有多余空格。

输入样例：

8 3 4
20 25 15 18 20 18 8 5

输出样例：

20 15
20 18 18 8
25 5

#include<iostream>
#include<queue>
#include<stack>
using namespace std;

int n, m, k;
queue<int> q;  // 存放推送器上顺序传过来的松针大小的队列
stack<int> box;  // 存放小盒子中松针大小的栈
stack<int> branch;  // 存放当前正在制作的松枝干上的松针大小的栈

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    cin >> n >> m >> k;  // 读取推送器上顺序传过来的松针数量、小盒子容量和松枝的容量
    
    // 读取推送器上顺序传过来的松针大小，并加入队列
    for(int i = 0; i < n; i++){
        int x;
        cin >> x;
        q.push(x);
    }
    
    while(1){
        int last = 0;  // 上一次插入的松针大小
        int cnt = 0;  // 当前已插入的松针数量
        
        // 如果小盒子已满，但推送器上取到的松针仍然不满足要求，将手中的松枝放到成品篮里，推送器上取到的松针压回推送器，开始下一根松枝的制作
        if(box.size() == m && (q.empty() || q.front() > box.top())){
            while(!branch.empty()){
                cout << branch.top() << ' ';
                branch.pop();
            }
            cout << '\n';
            box.pop();
            continue;
        }
        
        // 如果小盒子中最上面的松针不满足要求，但推送器上已经没有松针了，将手中的松枝放到成品篮里，开始下一根松枝的制作
        if(box.size() && box.top() != last){
            while(!branch.empty()){
                cout << branch.top() << ' ';
                branch.pop();
            }
            cout << '\n';
            box.pop();
            continue;
        }
        
        // 如果手中的松枝干上已经插满了松针，将之放到成品篮里，开始下一根松枝的制作
        if(cnt == k){
            while(!branch.empty()){
                cout << branch.top() << ' ';
                branch.pop();
            }
            cout << '\n';
            continue;
        }
        
        // 从小盒子中取出最上面的一片松针，如果小盒子为空，就从推送器上取一片松针
        int needle;
        if(box.empty()){
            needle = q.front();
            q.pop();
        }
        else{
            needle = box.top();
            box.pop();
        }
        
        // 将这片松针插到当前正在制作的松枝干的最下面
        branch.push(needle);
        last = needle;
        cnt++;
    }
    
    return 0;
}

以上就是队列的相关知识点以及考研408、企业面试的专项练习，在下一篇中我们将介绍排序算法。