现控散落知识点梳理【自用/最新】

发布时间：2023年12月20日

这里写目录标题

悬而未决之谜

?结合能控分解思考，非奇异线性变换会不会导致某变量的可控可观性发生变化？

事实上，进行线性变换（能控/能观分解）后，状态变量的物理意义已经发生变化。
原问题我想问的意思其实是，任给一个矩阵A，可否知道每个状态是否可观/可控，应该可以用PBH判据判断【不太确定】

?如图所示与时域结合时，传递函数是开环or闭环？

在这里插入图片描述
应该是对应的闭环传递函数，是直接连接输入和输出、没有反馈部分的

——但是要注意 在现控中往往没有开环/闭环概念

?对于一般状态，给出ABC，怎么判断每个变量的能控能观性？【非上三角/下三角】

回答：就是能控能观分解呗

状态函数结构图

要点🌟

  • 在每一个方框图之后加入变量x
  • 如果传递函数为高阶，可以部分分式展开，则展开
    • 若不可以，则组合设置两个状态变量，其中一个状态变量为另一状态变量的导数 x ˙ 1 \dot x_1 x˙1? 或者 使用反馈结构
  • 若展开后，分子还有项，则进行并联
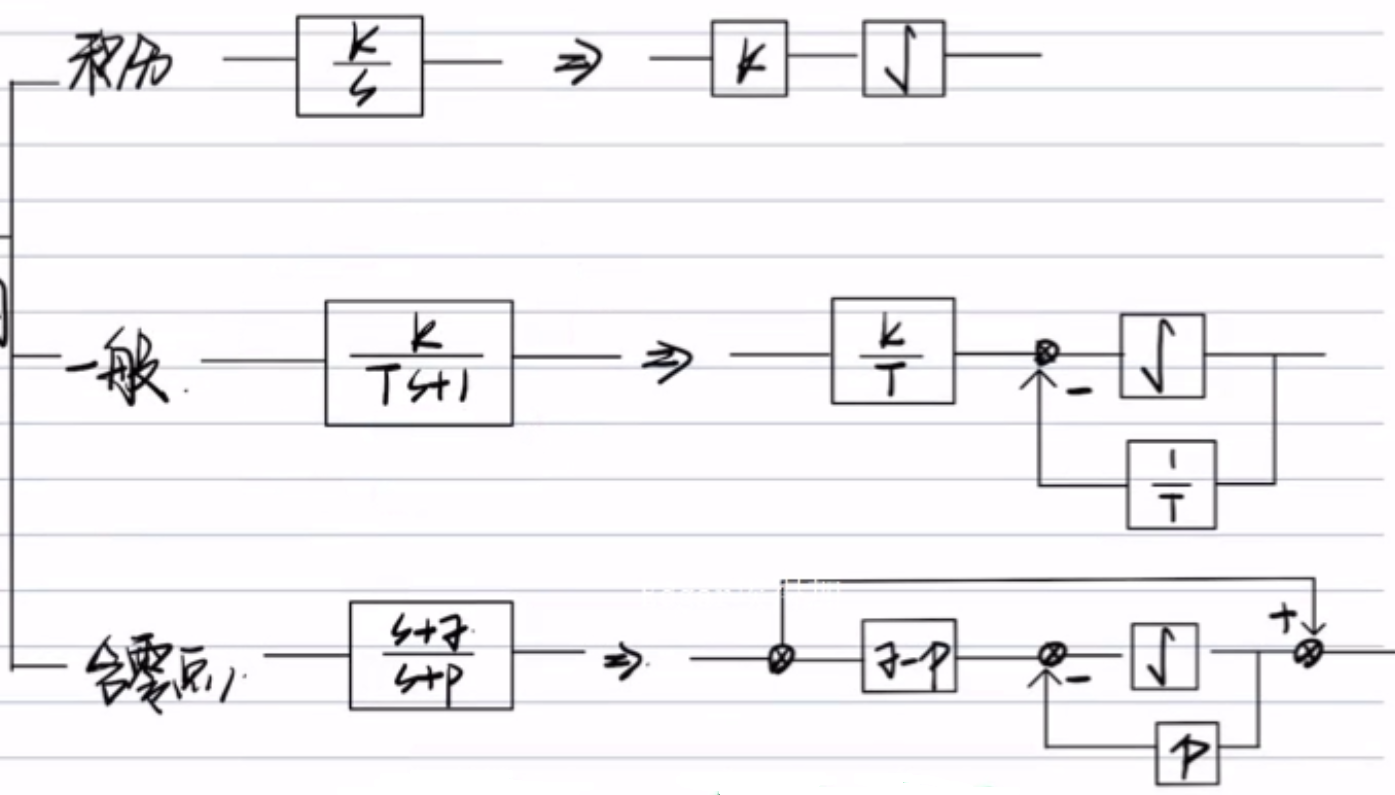
    在这里插入图片描述
  • 如上图所示，如果出现分子分母同阶，说明动态方程中的D可能不为0，y和u可能直接相关【其实就是上面结论的推论】

举例1 传递函数有分子-改并联+传递函数高阶分母-部分分式展开

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

注：上面的部分也可以改成积分环节和惯性环节串联

举例2 传递函数分母无法进行部分分式展开法 组合设置两个状态变量状态变量的导数

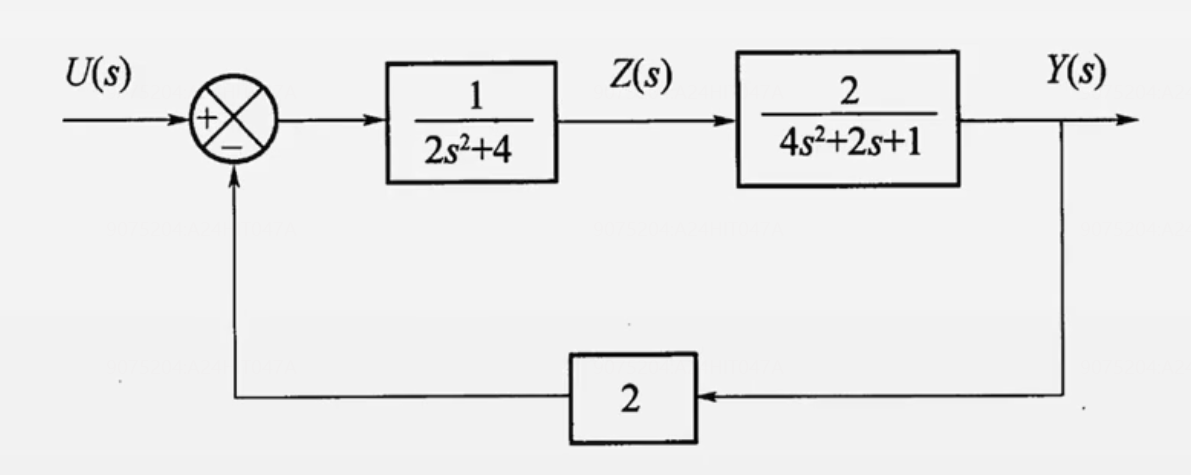
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

举例3 不可部分分式展开，也可以考虑用反馈环节

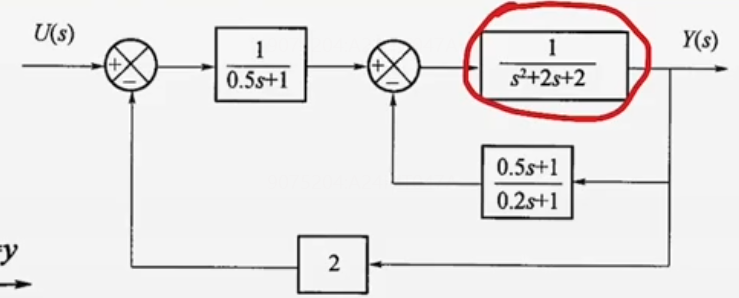
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

举例4 所有的惯性环节都可以用反馈环节代替之【这个例子也告诉我们有常数项时，变量的选取应该放在积分后而非整个传函后】

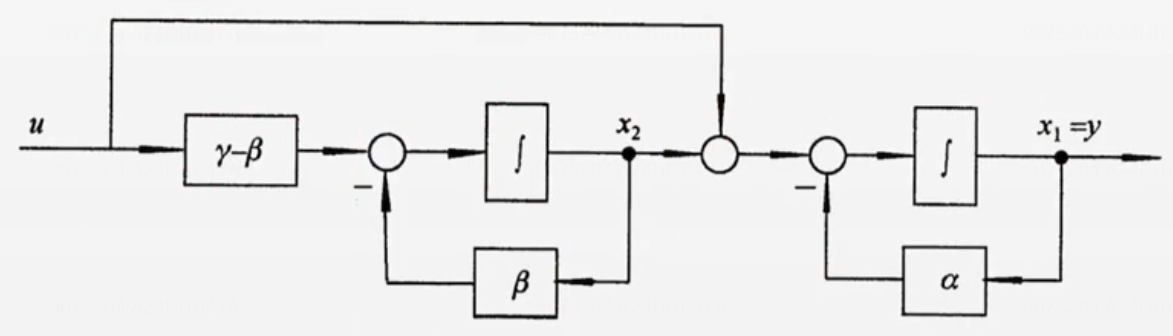
在这里插入图片描述

在这里插入图片描述

已知传递函数求状态方程矩阵

要点

  • 注意分母 s n s^n sn的最高阶前的系数是1
  • 可控型（I型）和可观型（II）型互为对称
  • 要掌握可控/可观/约旦阵的结构图形式

    能控结构图

    从输入唯一性和三个积分环节入手，确定三个变量的顺序
    【 x 3 x_3 x3?和输入有关，更靠近输入】
    在这里插入图片描述

    能观结构图

    从输出唯一性和三个积分环节入手
    【 x 3 x_3 x3?和输出有关，更靠近输出】（和能控性中的完全相反）在这里插入图片描述

    约旦标准型

    根据特征值数目不同，有不同条支路并联在这里插入图片描述

可控/可观/约旦阵的选取方式

  • 要了解可控/可观/约旦阵的状态变量选取方式
    • 能控选取方式
      { x 1 = y x 2 = y ˙ ? x n = y ( n ? 1 ) \left\{\begin{array}{c} x_{1}=y \\ x_{2}=\dot{y} \\ \vdots \\ x_{n}=y^{(n-1)} \end{array}\right. ? ? ??x1?=yx2?=y˙??xn?=y(n?1)?
    • 约旦选取方式
      { X 1 ( s ) = 1 s ? λ 1 X 2 ( s ) ? x ˙ 1 = λ 1 x 1 + x 2 X 2 ( s ) = 1 s ? λ 1 X 3 ( s ) ? x ˙ 2 = λ 1 x 2 + x 3 X 3 ( s ) = 1 s ? λ 1 U ( s ) ? x ˙ 3 = λ 1 x 3 + u X 4 ( s ) = 1 s ? λ 2 U ( s ) ? x ˙ 4 = λ 2 x 4 + u ? X n ( s ) = 1 s ? λ n ? 2 U ( s ) ? x ˙ n = λ n ? 2 x n + u \left\{\begin{array}{c} X_{1}(s)=\frac{1}{s-\lambda_{1}} X_{2}(s) \Rightarrow \dot{x}_{1}=\lambda_{1} x_{1}+x_{2} \\\\ X_{2}(s)=\frac{1}{s-\lambda_{1}} X_{3}(s) \Rightarrow \dot{x}_{2}=\lambda_{1} x_{2}+x_{3} \\\\ X_{3}(s)=\frac{1}{s-\lambda_{1}} U(s) \Rightarrow \dot{x}_{3}=\lambda_{1} x_{3}+u \\\\ X_{4}(s)=\frac{1}{s-\lambda_{2}} U(s) \Rightarrow \dot{x}_{4}=\lambda_{2} x_{4}+u \\ \vdots \\ X_{n}(s)=\frac{1}{s-\lambda_{n-2}} U(s) \Rightarrow \dot{x}_{n}=\lambda_{n-2} x_{n}+u \end{array}\right. ? ? ??X1?(s)=s?λ1?1?X2?(s)?x˙1?=λ1?x1?+x2?X2?(s)=s?λ1?1?X3?(s)?x˙2?=λ1?x2?+x3?X3?(s)=s?λ1?1?U(s)?x˙3?=λ1?x3?+uX4?(s)=s?λ2?1?U(s)?x˙4?=λ2?x4?+u?Xn?(s)=s?λn?2?1?U(s)?x˙n?=λn?2?xn?+u?

可控型表达式🌟🌟

在这里插入图片描述

可观型表达式🌟🌟

在这里插入图片描述

约旦/对角阵

普通对角

传递函数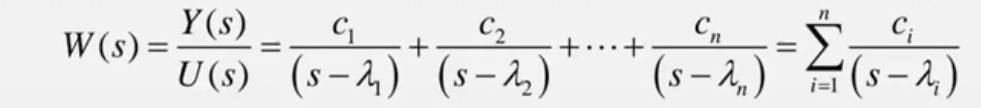在这里插入图片描述
矩阵类型
在这里插入图片描述

补充：如果发生零极点对消，且要求列写不能控不能观??

分析：如果产生零极点对消，相当于对应的状态变量“消失了”。因此之前的“全1行/列”中，该状态变量对应的1可以改为0
举例：传递函数如图
在这里插入图片描述

在这里插入图片描述

约旦对角【有重根】🌟🌟

传递函数
在这里插入图片描述
矩阵类型
在这里插入图片描述

举例1 传递函数上下齐次

此时应该先提取常数项，变成分母阶次比分子高，再进行操作
注意此时的输出，需要加u的常数项倍
在这里插入图片描述

离散状态空间及定常方程*极大概率不考

在这里插入图片描述
在这里插入图片描述

结构图

注意把积分环节改成延迟环节
在这里插入图片描述

连续系统离散化

在这里插入图片描述

离散系统状态转移方程

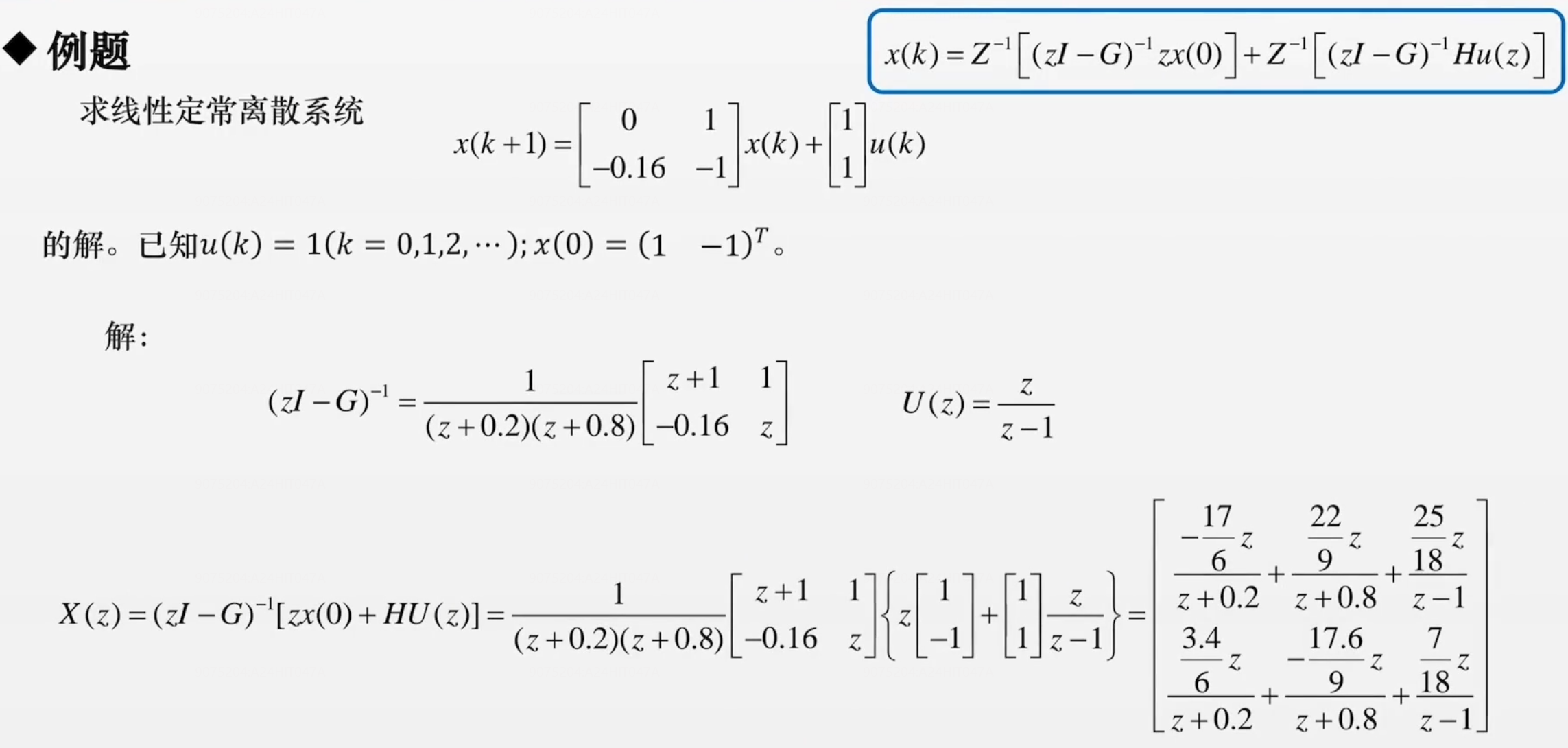
在这里插入图片描述

举例-x(0)已知时

在这里插入图片描述

Q：哈工大真题的2003-九已知x(t)求x(0)怎么做？

状态转移矩阵

求解状态转移矩阵的方法

拉式变换法🌟

e A t = Φ ( t ) = L ? 1 [ ( s I ? A ) ? 1 ] e^{A t}=\Phi(t)=L^{-1}\left[(s I-A)^{-1}\right] eAt=Φ(t)=L?1[(sI?A)?1]

对角矩阵

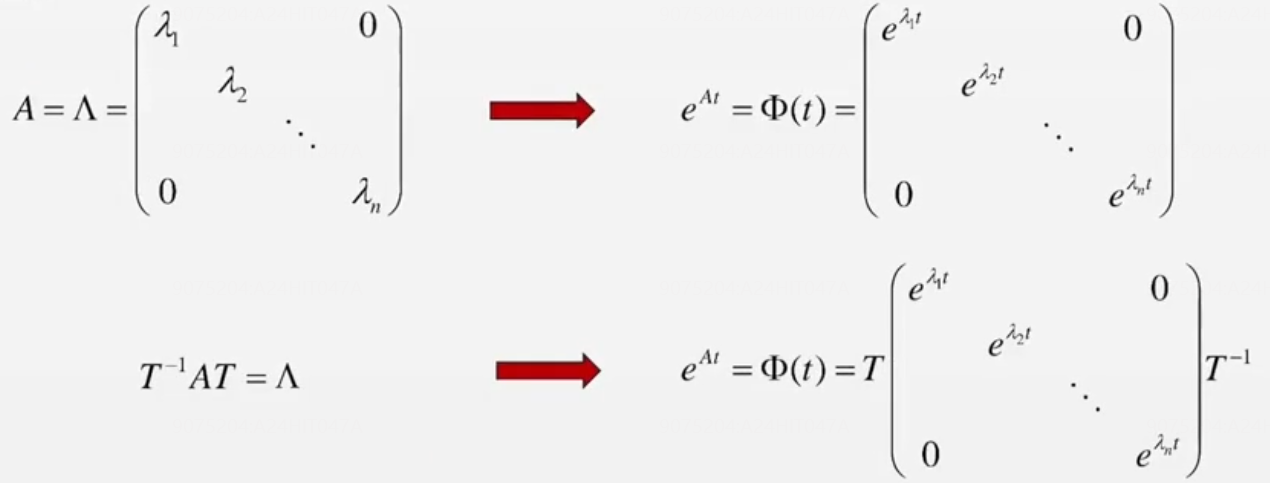
在这里插入图片描述

约旦阵

在这里插入图片描述

状态转移矩阵常用性质

在这里插入图片描述
Φ ( t 1 ) ? Φ ( t 2 ) = Φ ( t 1 + t 2 ) \Phi(t_1)\cdot\Phi(t_2) = \Phi(t_1+t_2) Φ(t1?)?Φ(t2?)=Φ(t1?+t2?)
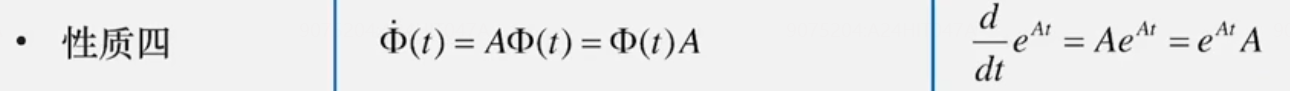
在这里插入图片描述

齐次方程的解🌟🌟

x ( t ) = Φ ( t ) x 0 = e A t x 0 , t > = 0 x(t)=\Phi(t)x_0=e^{At}x_0, t>=0 x(t)=Φ(t)x0?=eAtx0?,t>=0
在这里插入图片描述
结合拉式变换法，用反拉式变换轻松求得答案。

e A t = Φ ( t ) = L ? 1 [ ( s I ? A ) ? 1 ] e^{A t}=\Phi(t)=L^{-1}\left[(s I-A)^{-1}\right] eAt=Φ(t)=L?1[(sI?A)?1]【拉氏变换】

举例1 利用状态转移矩阵的一些性质

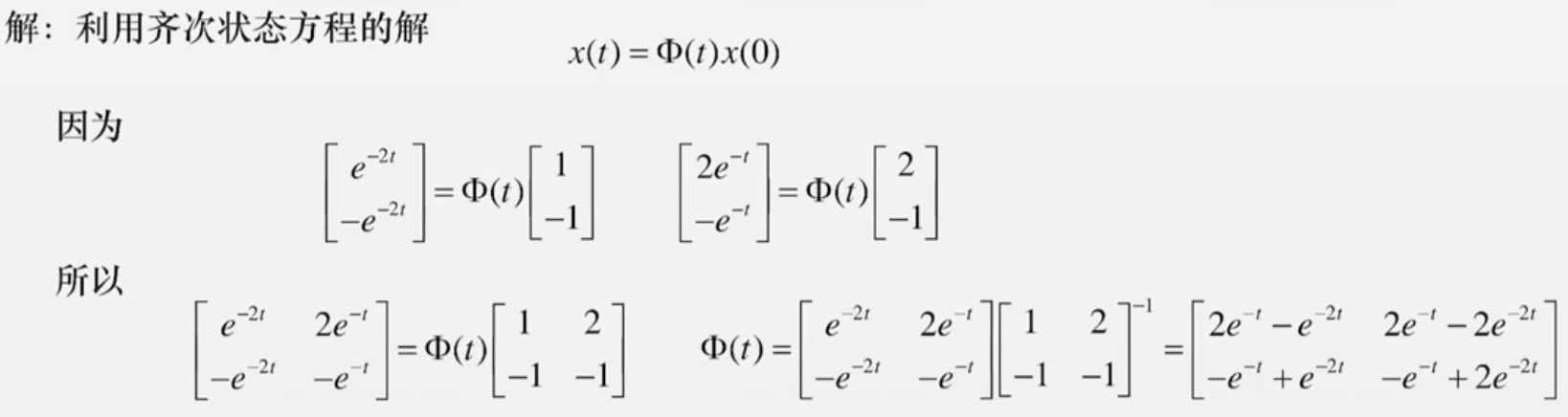
在这里插入图片描述
在这里插入图片描述

非齐次方程的解

拉式变换法【现推、不常用】

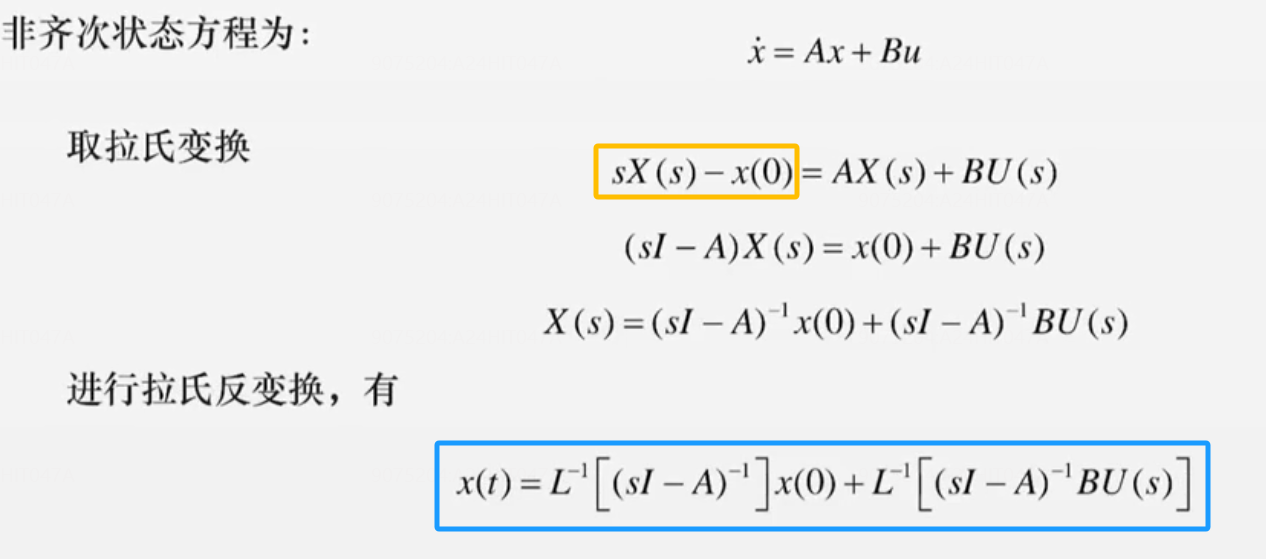
在这里插入图片描述

积分法【推荐掌握】🌟🌟

在这里插入图片描述

举例1 带输入矩阵解的时域表达式

在这里插入图片描述

举例2 带脉冲输入的时域表达式

在这里插入图片描述
第一步：求状态转移矩阵，注意拉氏反变换相关知识
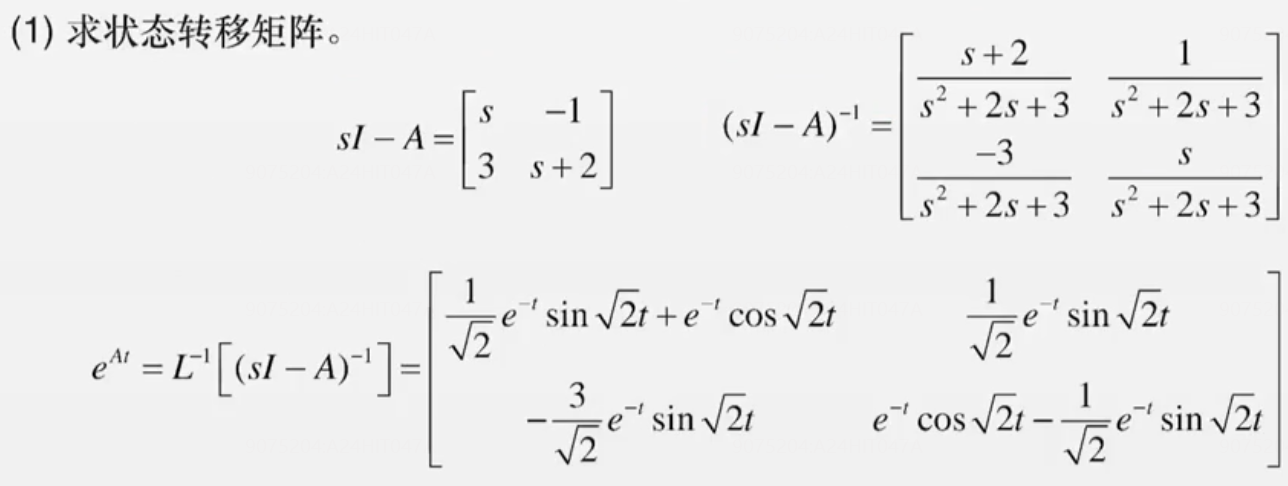
在这里插入图片描述
第二步：状态响应，【阶跃】结合【积分】极大优化运算
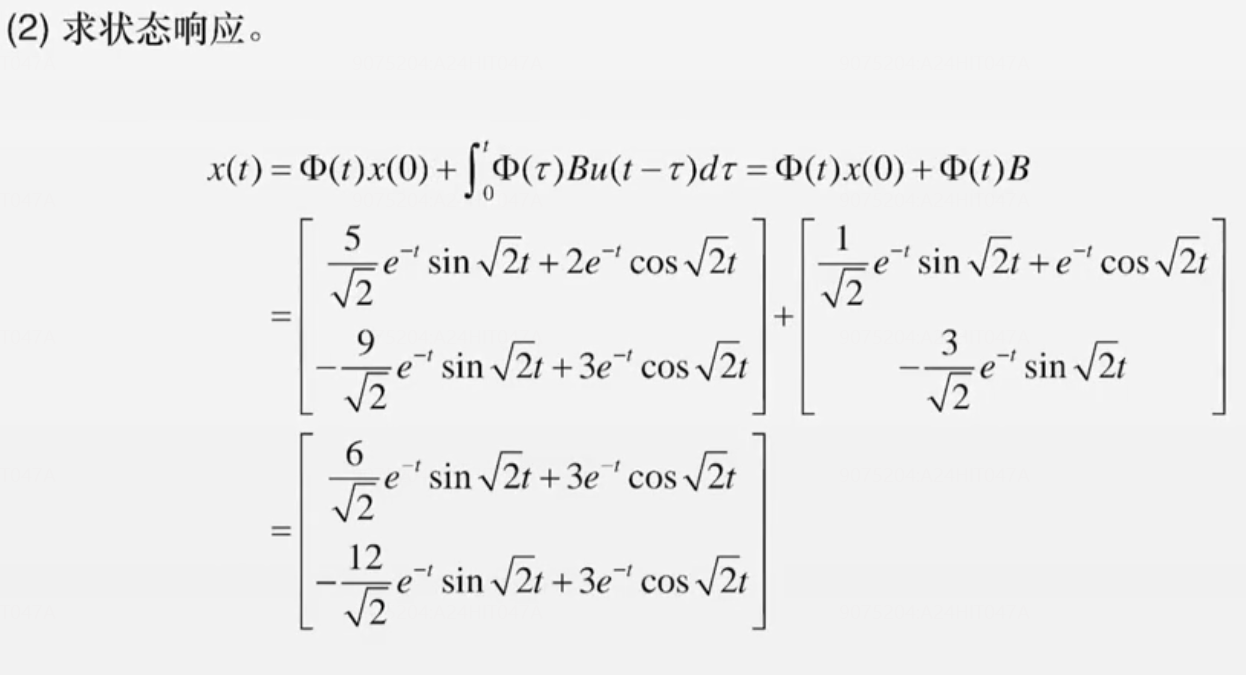
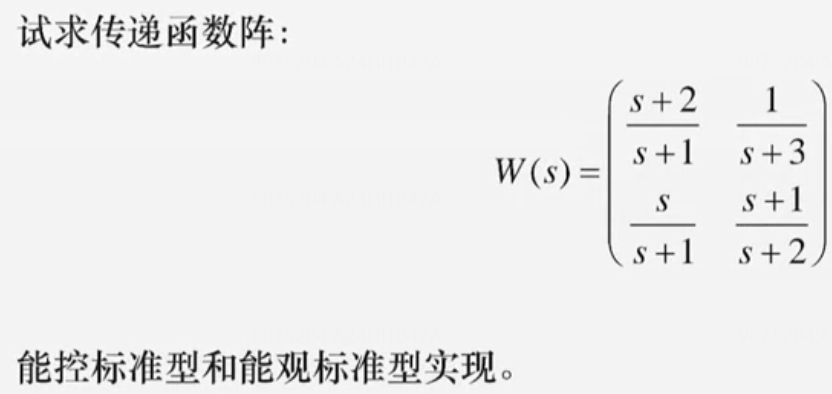
在这里插入图片描述

传递函数阵的实现问题

题型如下图所示：
在这里插入图片描述

要点：判断输入输出的矩阵行列数【Tops】🌟

G m × r G_{m\times r} Gm×r?

  • G阵的列数r对应u输入的列数r，G阵的行数m对应y输出的行数m，绝对不变🌟
  • 能控阵和能观阵实现可能有所不同：🌟
    对于A阵方阵，方阵的行数=列数=
    • 能控-n[分母阶次]*r[传函列数]；
    • 能观-n[分母阶次]*m[传函行数]
  • 原理还是标准型实现的原理，如果维数不够，乘对应的单位矩阵
  • 注意转置时，内部的每个小矩阵不转置
  • 总而言之，传递函数列少时，能控更好写；行少时，能观更好写

通解

  1. 提取常数使传函全都是真分式【之后常数部分作为传递函数中的矩阵 D D D】
  2. 提取公分母，还是按照常数、 s 1 s^1 s1、 s 2 s^2 s2升阶顺序排列

举例1 提取常数化成真分式后做题

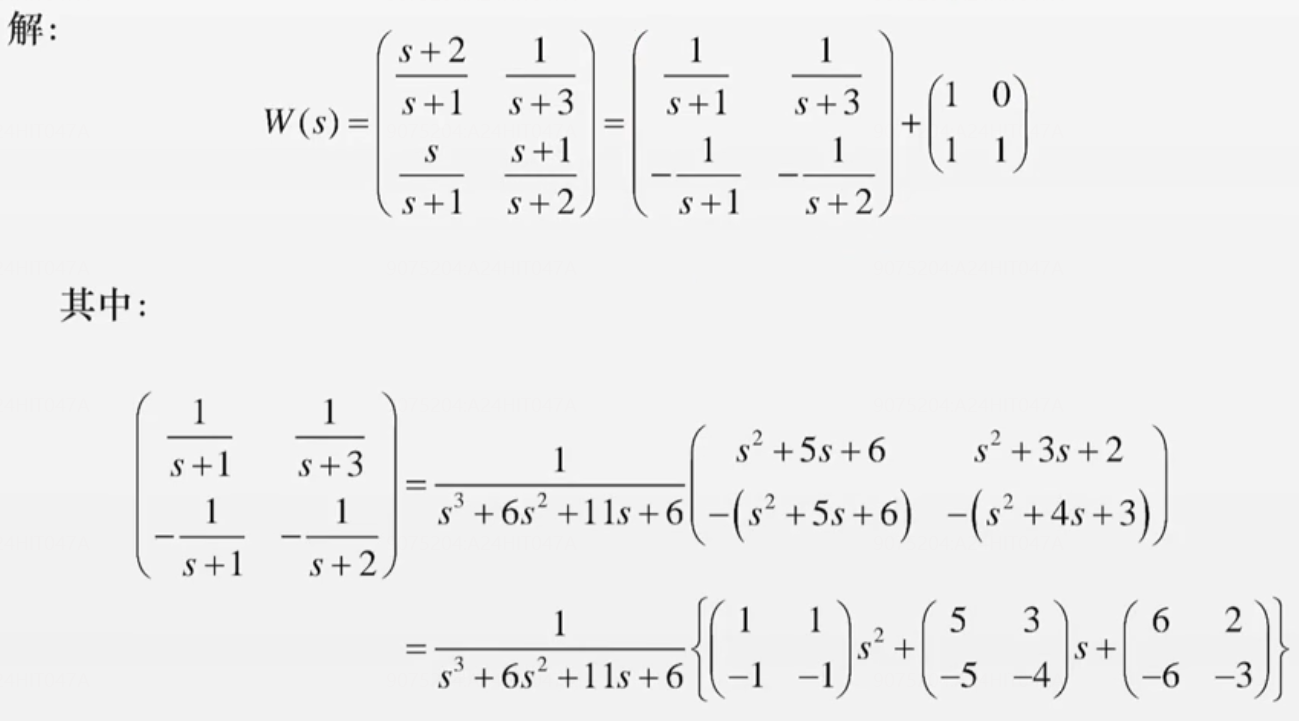
在这里插入图片描述
拆分
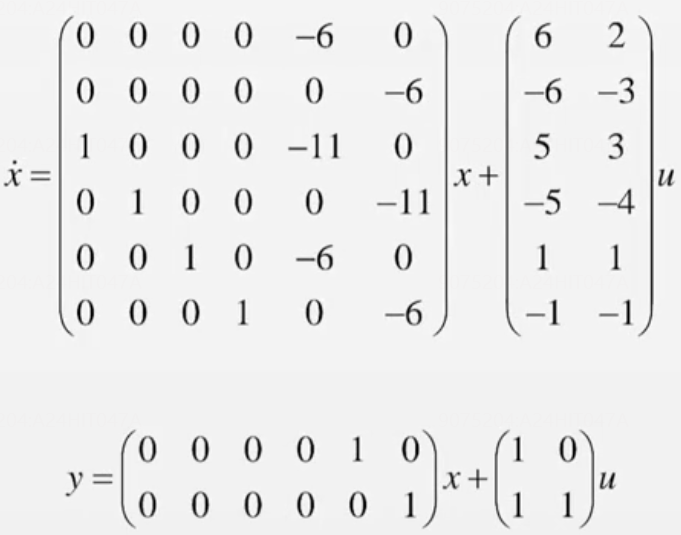
在这里插入图片描述
可控
在这里插入图片描述
可观
在这里插入图片描述

能控性与能观性

能控能观判据一览🌟🌟

Way1 单输入单输出下 零极点对消必然不是“可控可观”

Way2 能控能观性判据

可控性判断：
M = ( B , A B , A 2 B , . . . , A n ? 1 B ) M=(B, AB, A^2B, ..., A^{n-1}B) M=(B,AB,A2B,...,An?1B)
可观性判断：
N = ( C , C A , C A 2 , . . . , C A n ? 1 ) T N=(C, CA, CA^2, ..., CA^{n-1})^T N=(C,CA,CA2,...,CAn?1)T

Way3 对角阵/约旦阵

可控，同约旦块看最后一行B，可观看第一列C
相同特征值的不同约旦块之间需要线性无关才能保证可控/可观

Way4 PBH判据

在这里插入图片描述
在这里插入图片描述

变可控标准型🌟🌟

前提条件：系统能控
做题经验：求出特征值后，A可以由特征方程的系数得到而不用求 T c T_c Tc?；但是求C要费点劲（结合变换矩阵T）
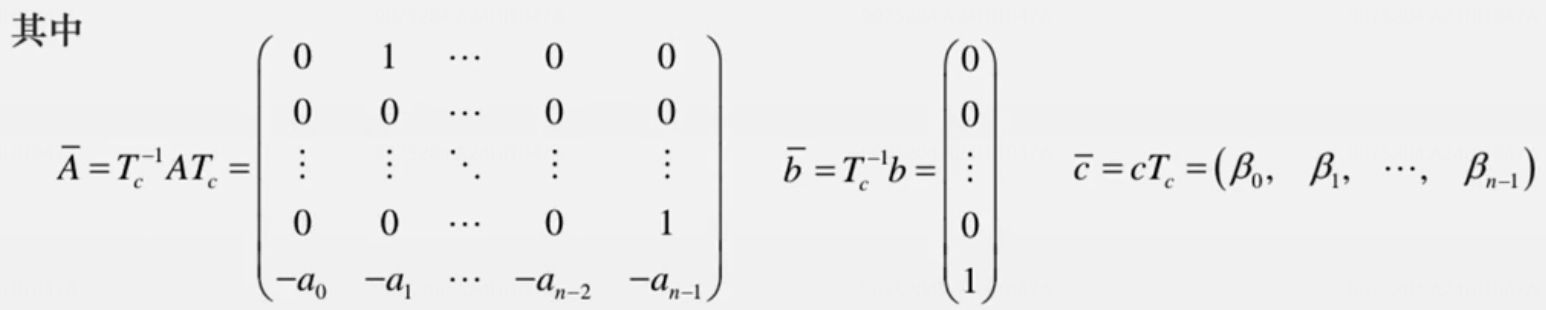
在这里插入图片描述【没有 a 0 a_0 a0?项】
在这里插入图片描述
在这里插入图片描述

举例 求一般矩阵（可控）的能控标准型

在这里插入图片描述

能控分解🌟🌟

在这里插入图片描述
其中， R c R_c Rc?的前 n 1 n_1 n1?列，是判别矩阵M中的任意线性无关的 n 1 n_1 n1?列，剩下的列任取，保证 R c R_c Rc?可逆即可
在这里插入图片描述

这里的可控针对的是变换后的状态变量，和原来的

变可观标准型🌟🌟

前提条件：系统能观
做题经验：求出特征值后，A可以由特征方程的系数得到而不用求T；但是求B要费点劲（结合变换矩阵 T 0 ? 1 T_0^{-1} T0?1?）
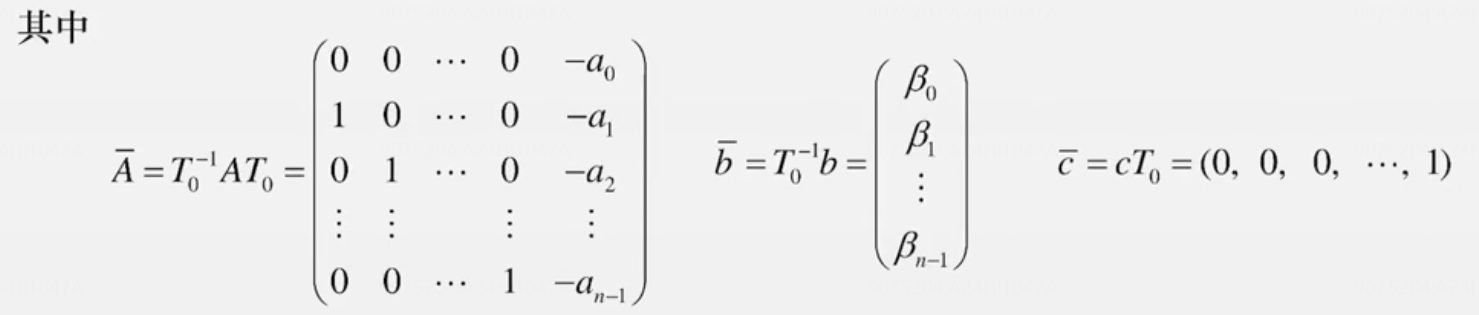
![在这里插入图片描述](https://img-blog.csdnimg.cn/8cf98344f7c443499d9062b0222b89a6.png =50 0x)
在这里插入图片描述
在这里插入图片描述

举例 求一般矩阵（可观）的能观标准型

在这里插入图片描述

能观分解🌟🌟

在这里插入图片描述
其中， R o ? 1 R_o^{-1} Ro?1?的前 n 1 n_1 n1?行，是判别矩阵M中的任意线性无关的 n 1 n_1 n1?行，剩下的行任取，保证 R o R_o Ro?可逆即可
在这里插入图片描述

举例1 进行能控+能观分解，即最小实现问题【较难，注意第二步线性变换的方式】

  • 思路
    相当于对系统进行能控性（能观性）分解后，再分别对两个部分进行能观性（能控性）分解
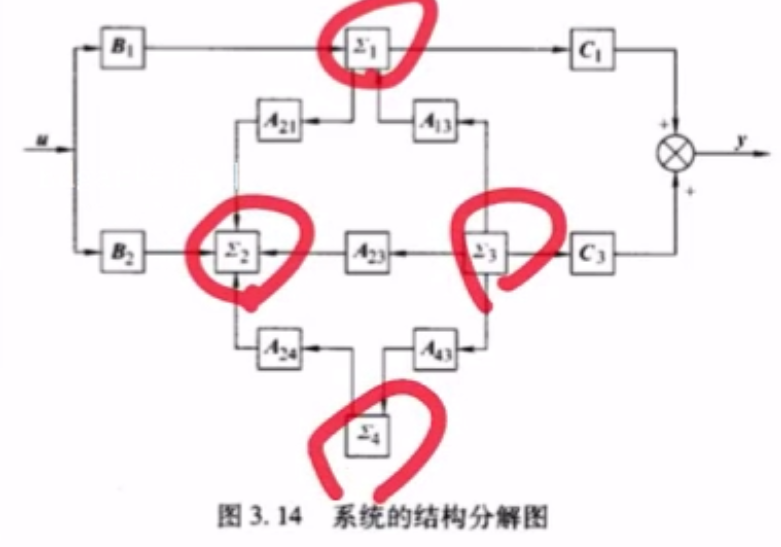
    在这里插入图片描述
    在这里插入图片描述

例题
在这里插入图片描述

  1. 能控性分解
    在这里插入图片描述
  2. 对能控部分进行能观性分解
    补充说明：如果能观性分解后，能控不能观的部分是一维的，即一个数【如本题】，那就看做“输入u”，直接左乘变换矩阵 R ? 1 R^{-1} R?1，不需要右乘R
    在这里插入图片描述
    【上面截图最后一行出错了】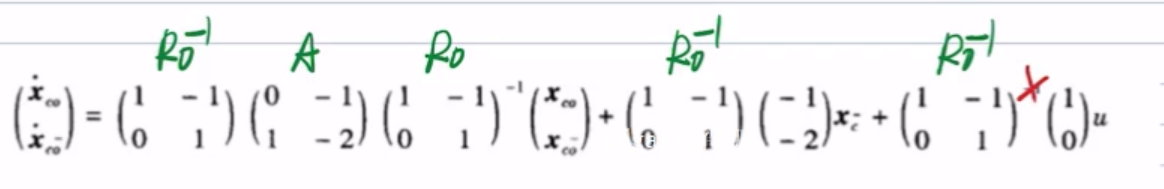在这里插入图片描述

Q 如果传递函数有零极点对消，那么一定不是最小实现

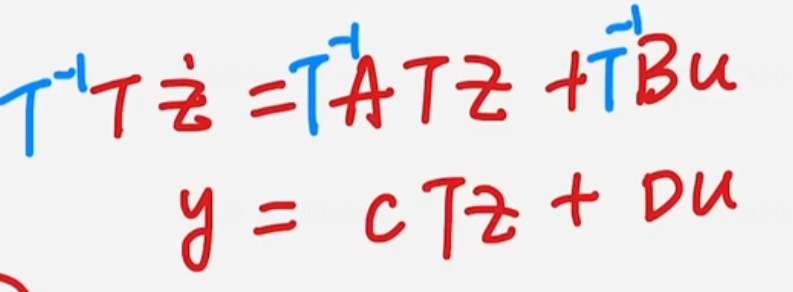
线性变换

基础知识🌟

线性变换的公式

要求：变换矩阵T非奇异
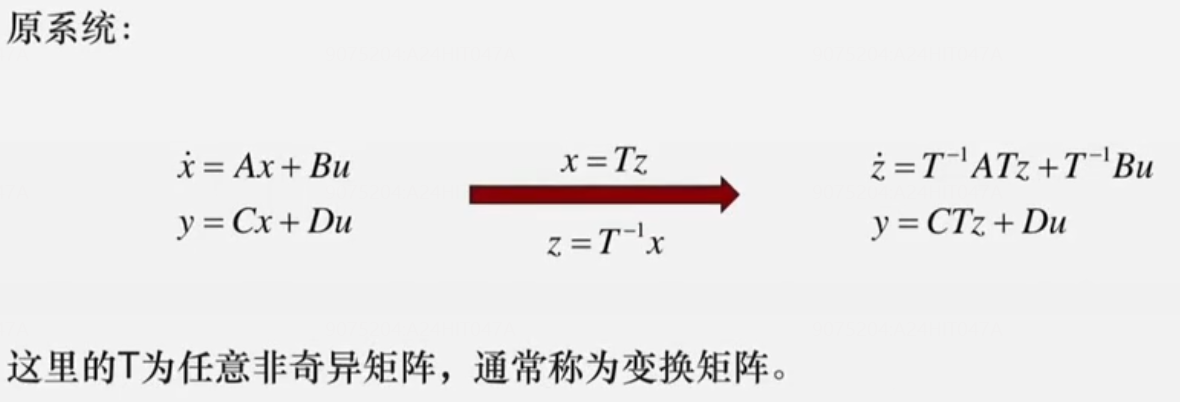
在这里插入图片描述

推导过程
在这里插入图片描述

线性变换性质

传递函数不变、特征值不变、系统【注意，是系统不是矩阵A】的可控可观性不变

变为对角阵（A可进行相似对角化）

对应：特征值无重根的情况
方法：找特征向量进行相似对角化

相似对角化中一个特例：A阵为友矩阵（仍要满足特征值无重根）

矩阵
在这里插入图片描述
对应变换公式
在这里插入图片描述

变为约旦阵（特征值有重根且A不可进行相似对角化）🌟

在这里插入图片描述

同样的特例：友矩阵

在这里插入图片描述
在这里插入图片描述

举例1 线性变换后求可观性?

在这里插入图片描述
经判断，A是友矩阵，线性变换为范德蒙德行列式
在这里插入图片描述
在这里插入图片描述

线性定常系统反馈问题

状态反馈【题目多，灵活】

结构图【反馈到输入后，B前】

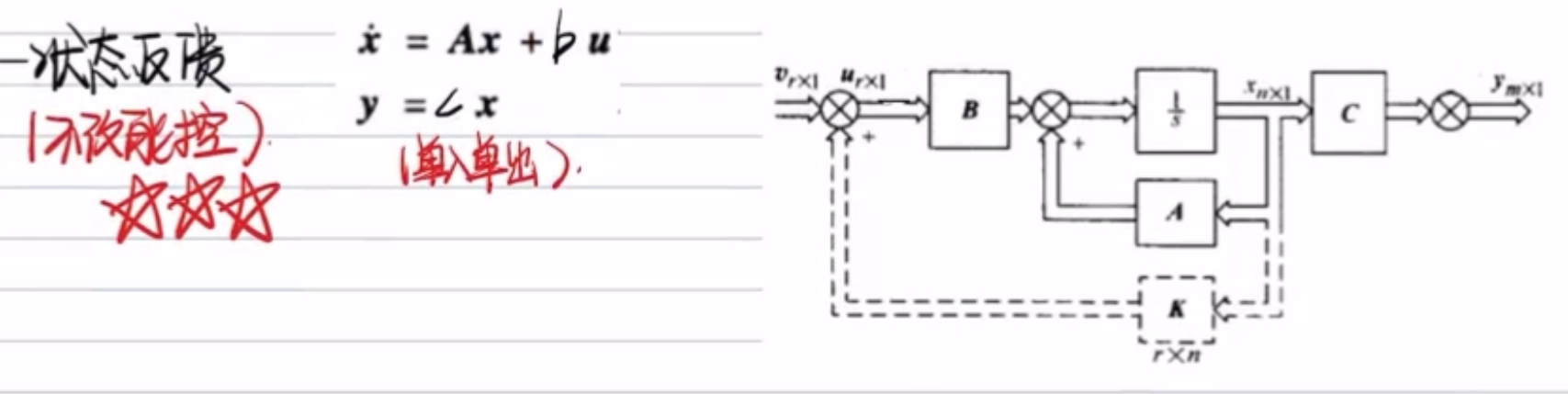
在这里插入图片描述

求解方法【官方，规范，必须遵守】?

  1. 判断系统是否满足能控性
  2. 列写反馈后的系统多项式【A+bK：正反馈 或者 A-bK：负反馈】其中K是1xm维未知向量
  3. 比较期望特征多项式和带参数的特征多项式的各项系数

绘图示例

在这里插入图片描述

技巧方法🌟【??本方法只适用于A为能控标准型情况】【状态观测器中该技巧对偶存在】

在这里插入图片描述
注意，k的下标和s前的系数是一致的，状态反馈后系统零点未改变
在这里插入图片描述

在此方法下…

在此方法下，分母就是特征多项式，分子不变，因为状态反馈不改变系统零点

举例1 状态反馈+结构图

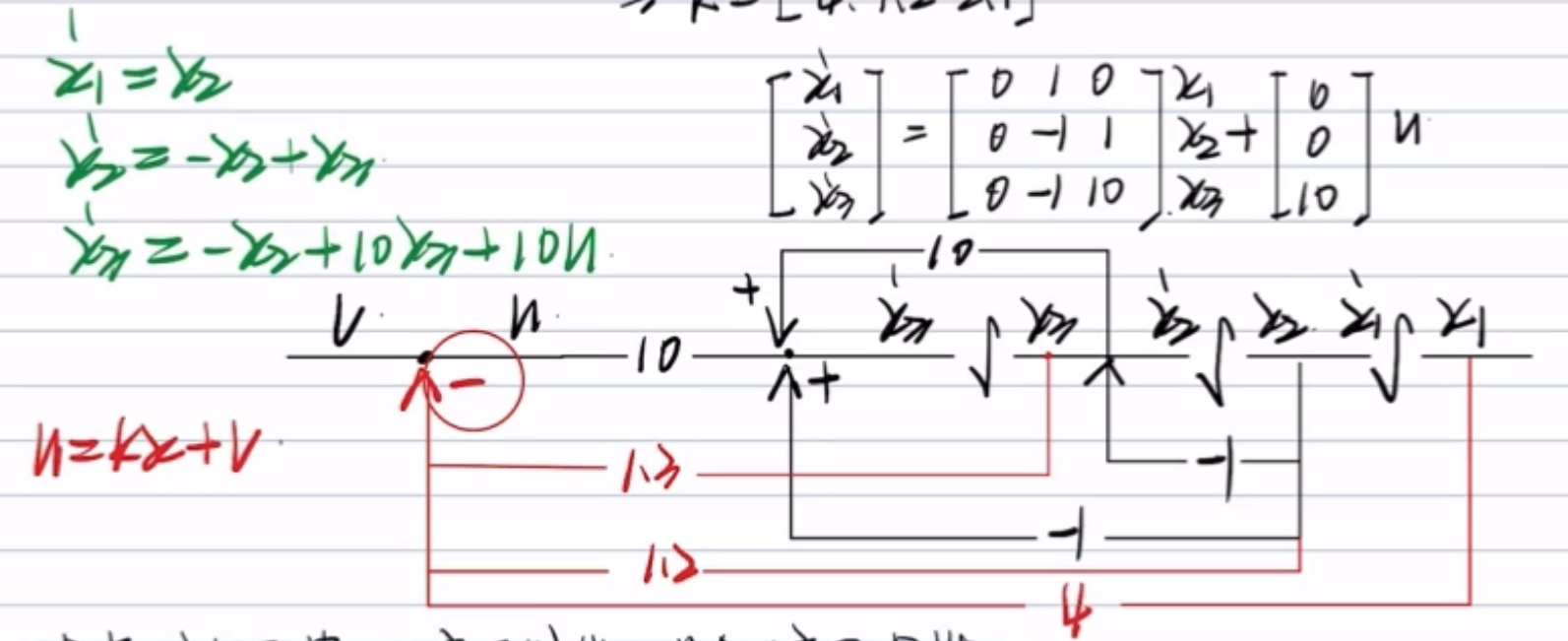
在这里插入图片描述

在这里插入图片描述

举例2 状态反馈+反馈后可观性

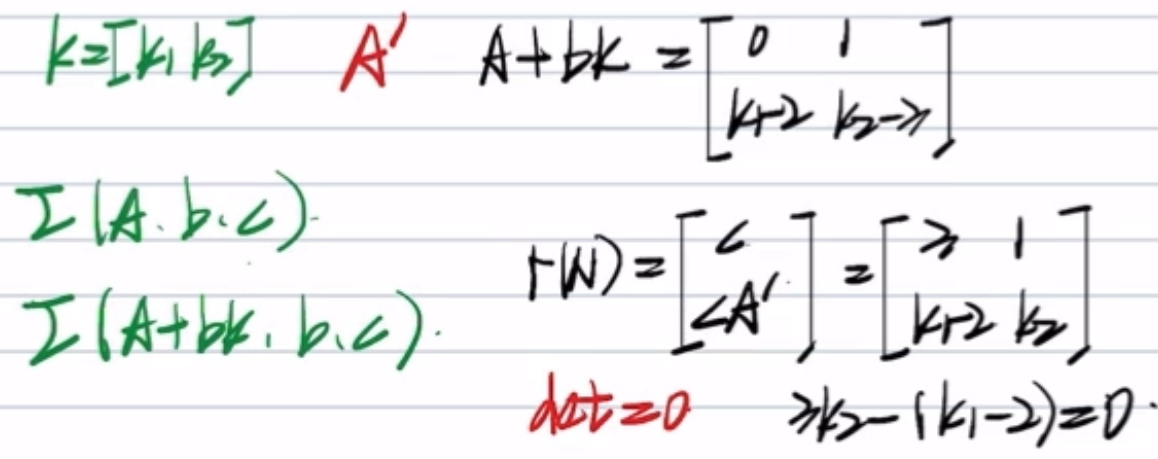
在这里插入图片描述
在这里插入图片描述

举例3 状态反馈+结构图&零极点对消

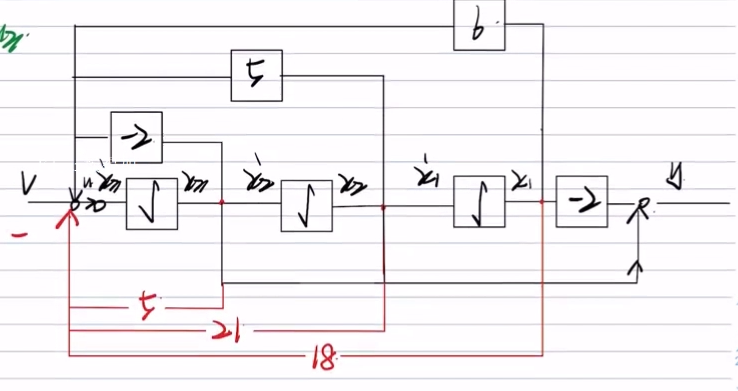
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

输出反馈*【考察的不多】

结构图【往往用下面的，反馈到状态变量导数前，B后】

在这里插入图片描述

求解方法【官方，规范，必须遵守】?

  1. 判断系统是否满足能观性
  2. 列写反馈后的系统多项式【A+Gc：正反馈 或者 A-Gc：负反馈】其中G是rx1维未知向量
  3. 比较期望特征多项式和带参数的特征多项式的各项系数

系统镇定【套路固定】

求解方法

进行能控分解后，系统镇定的充要条件是不可控部分特征值为负，因此基本套路如下：

  1. 能控分解，判断不能控部分特征方程是否均具有负实部
  2. 能控部分进行极点配置【随便配置，能控部分满足条件即可，不能控部分系数任意】
  3. ??将能控部分的状态反馈系数K‘转为原系统的状态反馈系数K（右乘 T c ? 1 T_c^{-1} Tc?1?）

    转换方法如下
    在这里插入图片描述
    类似地，输出反馈的话是左乘 ( T o ? 1 ) ? 1 (T_o^{-1})^{-1} (To?1?)?1【都是对：能直接得到的矩阵 求逆，一个是左乘，一个是右乘】

求解方法② 利用PBH判据*非主流

参考上面的可控性判断，主流方法是判断不可控的部分是否稳定，这个是判断不稳定的部分是否可控

举例1 系统镇定+能控分解后的状态反馈向原状态反馈的转变🌟🌟?

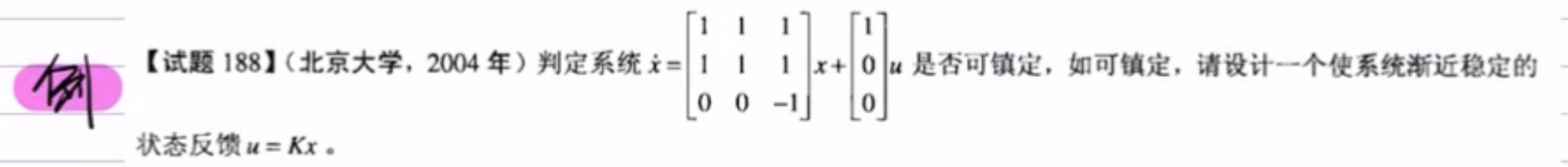
在这里插入图片描述

  1. 能控分解
    在这里插入图片描述

  2. 状态反馈配置可控部分
    在这里插入图片描述

  3. 将能控分解矩阵对应的反馈系数 K K K转为线性变换前反馈系数 K 0 K_0 K0?
    在这里插入图片描述

解耦*【从未考察】

求解方法

纯粹就是套模板

  1. 判断每一个输入对应的di
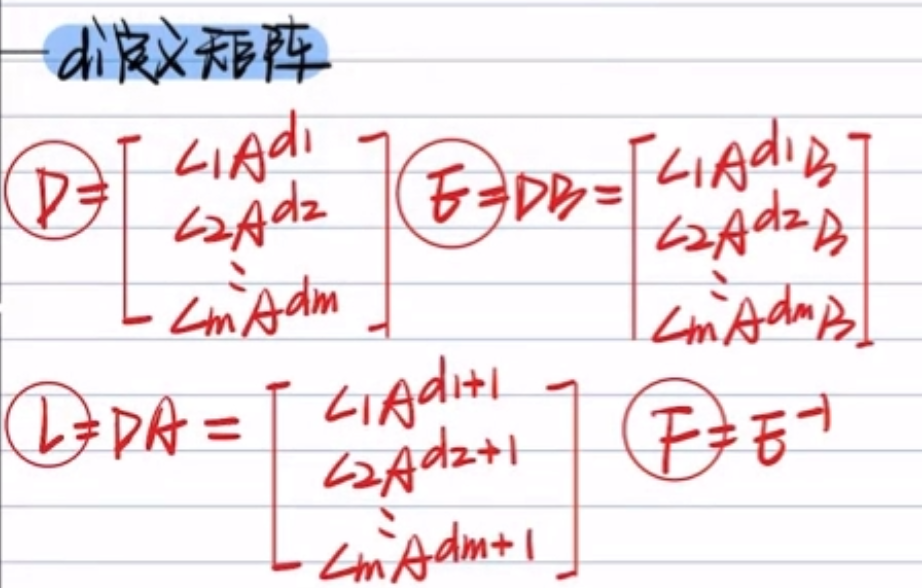
    在这里插入图片描述
  2. 代公式
    在这里插入图片描述
  3. 判别
    在这里插入图片描述

状态观测问题

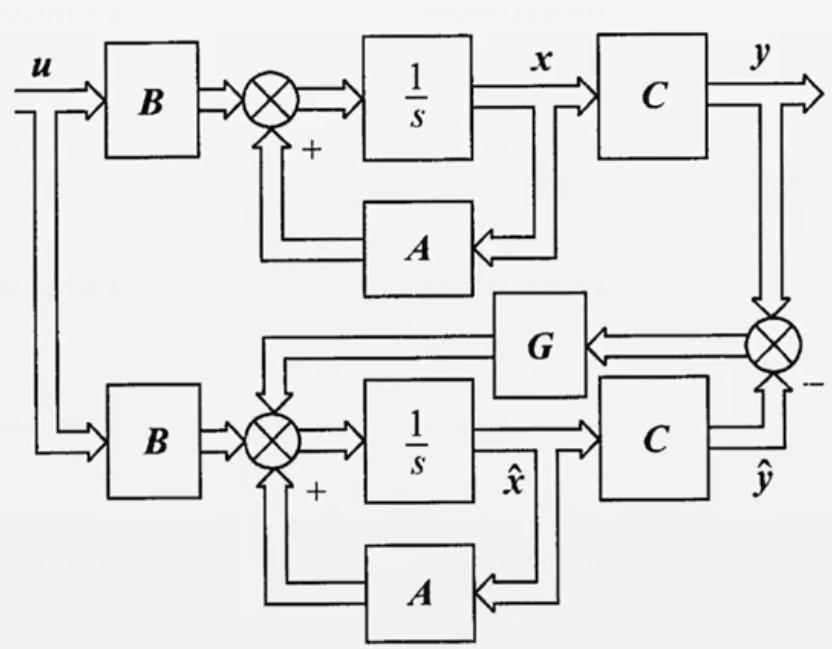
全维状态观测

结构图示意

本质上是状态反馈
在这里插入图片描述
??另一种表述
在这里插入图片描述

举例1 全维观测器+列写观测器方程

在这里插入图片描述
在这里插入图片描述

举例2 状态观测器（输出反馈）+状态反馈

在这里插入图片描述
设计观测器和进行状态反馈实际上是完全分开的

  1. 设计观测器
    在这里插入图片描述
  2. 设计状态反馈【可以考虑使用技巧方法】
    在这里插入图片描述
  3. 模型类似于下图：
    动态方程：
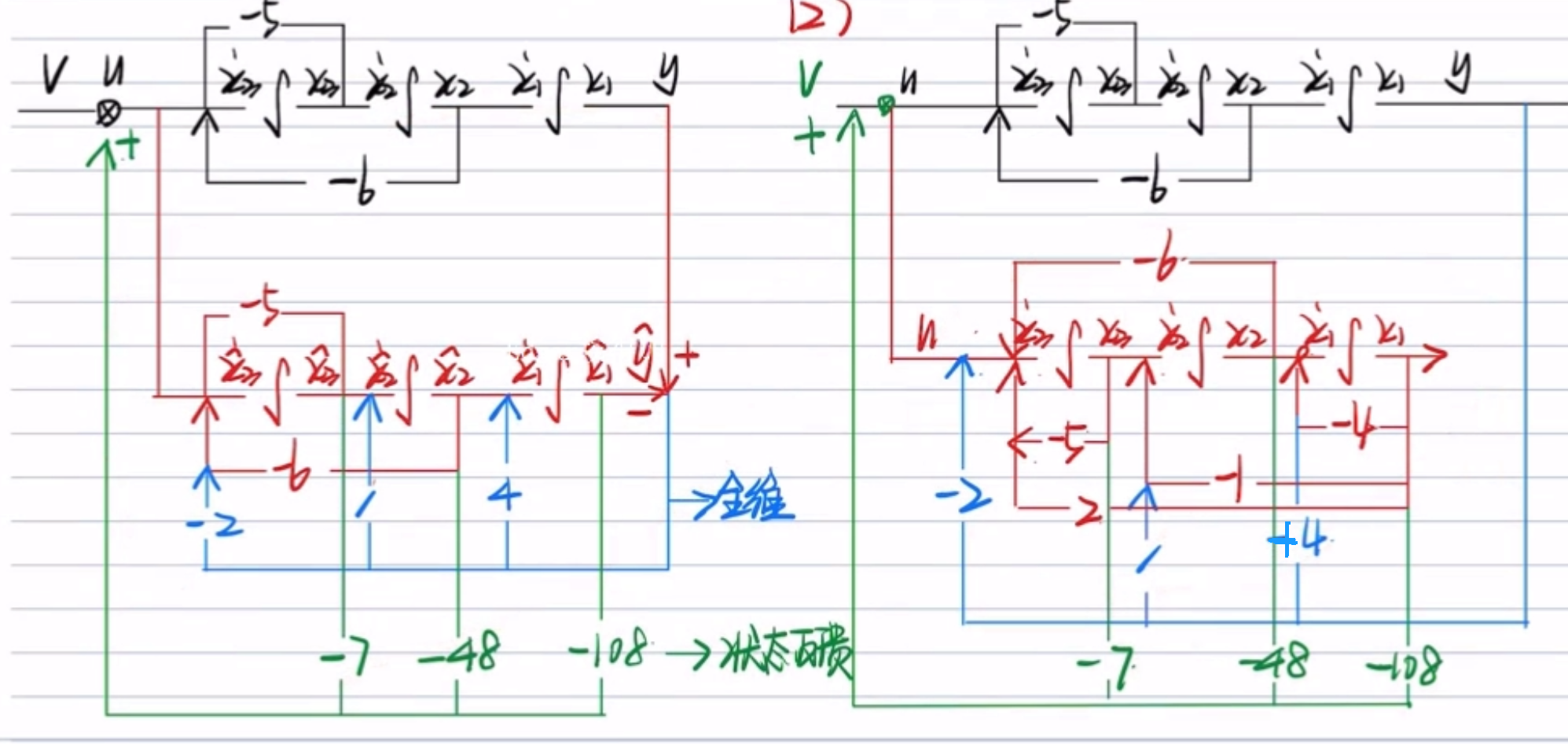
    在这里插入图片描述
    两种模型
    在这里插入图片描述

全维状态观测器的误差求解

在这里插入图片描述

在这里插入图片描述

举例【实质上是齐次方程求解问题】

在这里插入图片描述
注意最后一步取了一个模长

一个结论：极点距离虚轴越远，趋于稳定的速度越快，调节时间也就越快。

降维观测器

原理是利用通过调整输出对应的输出矩阵，可以获得一部分状态变量的观测值，从而减小传感器的数量等等。

Step01 设计 T ? 1 T^{-1} T?1，线性变换将输出矩阵调整成(0,0,I)形式

类似能观分解，能观分解中的矩阵选择，都是“一部分取原来的，一部分保证非奇异”
区别在于，可观分解是判据阵 前m-1行，这个是输出阵 后m行

在这里插入图片描述
T ? 1 T^{-1} T?1满足以下要求：最后m行为原输出矩阵C，上面的其他行任取，保证非奇异即可
然后以T为非奇异线性变换矩阵，进行线性变换

通常情况下，对输出y相关变量进行矩阵操作时，往往直接得到的是逆

完成线性变换后，可将A矩阵视为 A 11 ￣ , A 12 ￣ , A 21 ￣ , A 22 ￣ \overline{A_{11}},\overline{A_{12}},\overline{A_{21}},\overline{A_{22}} A11??,A12??,A21??,A22??【加横线代表和之前不一样】

Step02 设计降维状态观测器

按照 A 11 ， A 21 A_{11}，A_{21} A11?，A21?进行极点配置
f ( λ ) = det ? ( λ I ? ( A 11 ￣ ? G A 21 ￣ ) ) f ? ( λ ) = ( λ ? s 1 ) ( λ ? s 2 ) . . . ( λ ? s n ) \begin{array}{l} f(\lambda)=\operatorname{det}\left(\lambda I-\left(\overline{A_{11}} -G\overline{A_{21}}\right)\right) \\ f^{*}(\lambda)=(\lambda-s_1)(\lambda-s_2)...(\lambda-s_n) \end{array} f(λ)=det(λI?(A11???GA21??))f?(λ)=(λ?s1?)(λ?s2?)...(λ?sn?)?

Step03 套公式🌟🌟

在这里插入图片描述

这么做的原因是，原来的表达式里存在 y ˙ \dot y y˙?，不好求解 在这里插入图片描述

Step04 变回原有系统

上一步结果左乘 T T T
x ^ = T x ￣ ^ \hat {x} = T \hat{ \overline{ x}} x^=Tx^

举例1 降维观测器经典例题

在这里插入图片描述
Step01 能观性判断+变换矩阵设计
在这里插入图片描述
Step02 设计降维观测器
在这里插入图片描述
Step03 代入两个公式

Step04 线性变换变回去
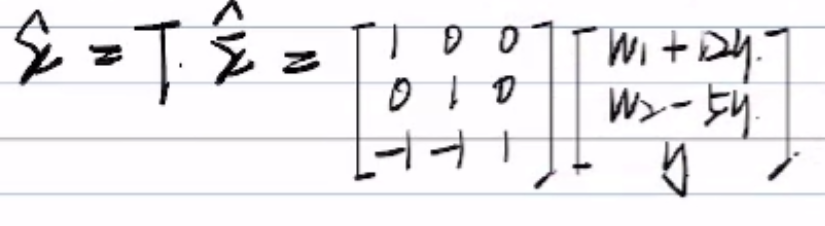
在这里插入图片描述

不熟练公式记录

状态方程非齐次求解【积分形式】
状态方程齐次求解和 e A t e^{At} eAt表达式书写
一般矩阵化能控标准型

文章来源:https://blog.csdn.net/weixin_51772802/article/details/134233102
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章