一个实例让你初识图像卷积

本篇文章参考李沐老师动手深度学习,只作为个人笔记.

前言

一、卷积

二、回顾全连接层

三.全连接层到卷积

四.图像的边缘检测

1.定义互相关运算函数

2.卷积层,与一维一样,把它当成一种运算就好理解了

3.图像中目标的边缘检测

五.学习由X生成Y的卷积核

总结

---

---

前言

在学习卷积神经网络之前我们已经了解了线性神经网络,这里我们简单回顾一下,从我们的线性回归,,softmax回归,多层感知机,模型的选择,欠拟合和过拟合,以及解决过拟合的两种方法,分别是:权重衰退和暂退法(dropout),前向传播,反向传播,模型的初始化等一系列知识,终于我们要学习卷积神经网络,从全连接层到卷积,本文基于前面我们对线性神经网络的了解,进一步扩展到卷积神经网络.

---

一、卷积

卷积（Convolution）卷积是一种积分变换的数学方法，与傅立叶变换有着密切的联系。 在数字信号处理、通信系统、光学系统、神经网络计算许多方面得到了广泛应用。

严格来说，卷积层是个错误的叫法，因为它所表达的运算其实是互相关运算（cross-correlation），而不是卷积运算。在卷积层中，输入张量和核张量通过互相关运算产生输出张量。

这里我就不在进行复杂的数学原理来介绍,大家要想深入研究可以搜索一下,在这里我就简单介绍一下具体如何操作就行了.

二、回顾全连接层

我们把32*32*3的图像直接拉成3072*1的输入(这里的32*32*3表示的是三通道的大小为32*32的图像)

三.全连接层到卷积

这里的输入和卷积核都是三维的,我们首先来拿一个二维的来举例子.

通过上图我们就很好理解,其实在运算时,实际上就是将和函数也就是我们所给的卷积核,扣在图像上然后对应位置相乘在相加之后输出,以相同操作遍历整张图,所得到的结果也就是我们输出的结果.

我们这里直接总结一下公式,就是当图片时N*N大小的,卷积核维F*F大小的,stride表示步长(就是遍历图片时我们要移几格),最后我们得到的输出图像为(N-F)/步长 +1.例子如上图的例子大家算一下就好理解了.

四.图像的边缘检测

如果大家学过一点数字图像处理,这里就比较好理解了,没学过也没关系很简单的.

1.定义互相关运算函数

import torch
from torch import nn
from d2l import torch as d2l

def corr2d(X, K):  #@save
    """计算二维互相关运算"""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

这段代码就是我们求卷积得到我们的输出结果的过程.

我简单介绍一下,能看懂的直接可以跳过.

首先我们输入我们的X即我们的图像,K即我们的卷积核.

Y则是我们通过卷积运算得到得结果.

Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))

这里我们先声明一个输出结果得框架,这个输出结果框架得大小,就是根据上面得公式就得到了,我们默认得步长为1.

然后就是两层for loop来计算输出结果,与上面我们给的例子操作相同.

接下来我们有了计算互相关运算函数来验证我们上面的例子是否正确.

X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
corr2d(X, K)

输出结果:

2.卷积层,与一维一样,把它当成一种运算就好理解了

class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

3.图像中目标的边缘检测

首先我们生成一个带边缘的数据.

X = torch.ones((6, 8))
X[:, 2:6] = 0
X

带边缘就是1到0,或者0到1,这就表示边缘.

之后定义我们的卷积核.这个是可以检测垂直方向的边缘的,大家可以试着乘一下就会发现之没变化的地方得到的结果是0,变换的地方得到的结果非0.

K = torch.tensor([[1.0, -1.0]])

最后得到我们的输出结果.

Y = corr2d(X, K)
Y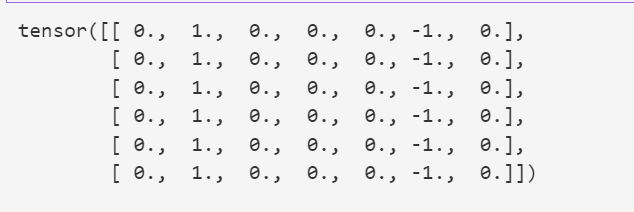

发现边缘的部分已经被检测出来了.

corr2d(X.t(), K)

将图像转置一下在输出结果我们发现无法检测出边缘.简单想想很好理解的.转置以后水平方向是没有梯度变化的.

五.学习由X生成Y的卷积核

刚才我们通过已有图像和给定卷积核得到我们的输出结果,那么我们如何根据图像X与输出结果Y去得到我们的卷积核呢?

# 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)

# 这个二维卷积层使用四维输入和输出格式（批量大小(照片数量)、通道、高度、宽度），
# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2  # 学习率

for i in range(10):
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    # 迭代卷积核
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch {i+1}, loss {l.sum():.3f}')

这里我们损失函数就用相差的平方,采用梯度下降法进行求解.

在10次迭代之后，误差已经降到足够低。现在我们来看看我们所学的卷积核的权重张量。

conv2d.weight.data.reshape((1, 2))

可以看到与我们之前所给定的卷积核还是相近的.

这个例子与线性回归应用梯度下降算法求解非常类似.

线性回归应用梯度下降法-CSDN博客

---

总结

本文简单介绍了卷积及相关操作,以及通过一个小例子帮助大家更好的初步了解卷积神经网络,希望能够帮助到大家.