[蓝桥杯学习] ST表
发布时间:2024年01月07日
RMQ问题

ST 表

用状态 s[i][j] 记录区间长度为 2^j 的长度的区间的最大值
所以状态转移方程就是 st[i][j] = max( st[i][j-1] , st[i+(1 << (j-1))][j-1] )
注意状态转移的方向,保证区间合法性(i+2^j? 不能超过数组大小)
写完这些后,定义好第一个,就可以从前往后进行计算
用ST表进行区间查询
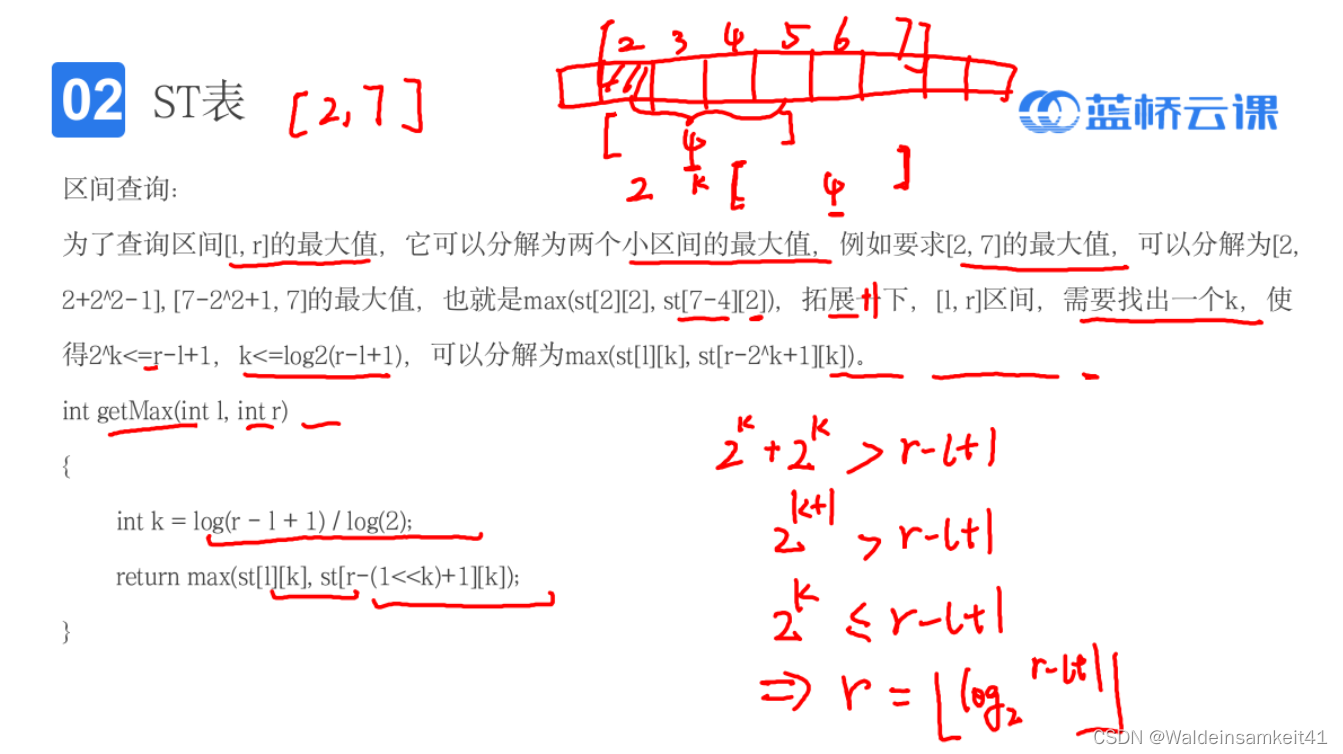
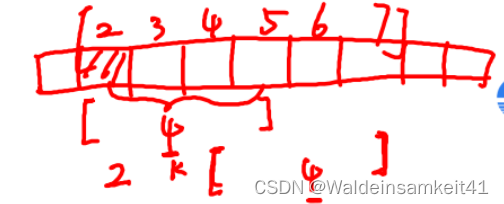
ST表存储的区间是2的整数倍,所以要计算的是,如何从要求的区间,到ST表存储的区域。
要寻找一个k,如果满足以下的大小关系,
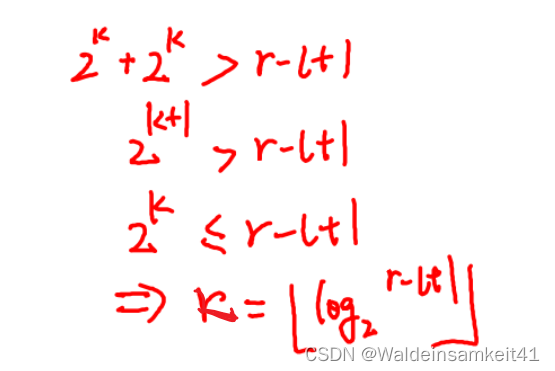
就可以取两个区间的最大值 max(st[l][k],st[r-(1<<k)][k]),这两个区间是囊括了整个要求的区域。
k值的具体计算是,把(r-l+1)对2求对数,并向下取整,可以用强制类型转换来实现。
求区间最大值的代码
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
#define ll long long
const int N = 5e5 + 5;
int n,q;
ll a[N];
ll st[N][21];
ll getMax(int l,int r)
{
//计算k,区间长度对2取对数
int k = log(r-l+1)/log(2);
return max(st[l][k],st[r-(1<<k)+1][k]);
}
int main()
{
// 请在此输入您的代码
cin >> n >> q;
for(int i = 1 ; i <= n ; i++)
{
int x;
cin >> x;
a[i] = x;
}
//构造ST表
//1.初始化
for(int i = 1 ; i <= n ; i++) st[i][0] = a[i];
//2.利用状态转移方程求ST表
for(int j = 1 ; j <= 20 ; j++)
{
for(int i = 1 ; i <= n ; i++)
{
if(i + (1<<j) -1 <= n) //不要忘记-1,是要区间长度为 2^j 的
{
st[i][j] = max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}
}
}
//3.利用ST表来求区间最大值
while(q--)
{
int l,r;
cin >> l >> r;
cout << getMax(l,r) <<'\n';
}
return 0;
}
文章来源:https://blog.csdn.net/weixin_73512213/article/details/135442160
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 贝塞尔曲线
- 【Linux】Ubuntu系统的基础操作和使用
- 机器学习分类模型
- Spark应用程序的结构与驱动程序
- [算法]使用aes进行数据加密
- 1月11日代码随想录513找树左下角的值
- oracle 补齐数字长度 to_char踩坑
- C语言报错:declaration does not declare anything
- 校友交流论坛(JSP+java+springmvc+mysql+MyBatis)
- FEP水质取样器应用环境检测无溶出析出深水取样器