基于循环神经网络长短时记忆(RNN-LSTM)的大豆土壤水分预测模型的建立

本研究的目的是开发一种未来的土壤水分(SM)预测模型，以根据土壤水分随天气条件的变化来决定是否进行灌溉。
传感器用于测量距表层土壤10 cm、20 cm和30 cm深度的土壤水分和土壤温度。
以10 cm至30 cm深度的土壤湿度和土壤温度以及天气数据作为输入变量，对最优变量组合进行了研究。
利用时间序列数据建立了预测SM的循环神经网络长短时记忆(RNN-LSTM)模型。
以损耗值和决定系数(R2)值作为评价模型性能的指标，并利用两个验证数据集对不同条件进行测试。
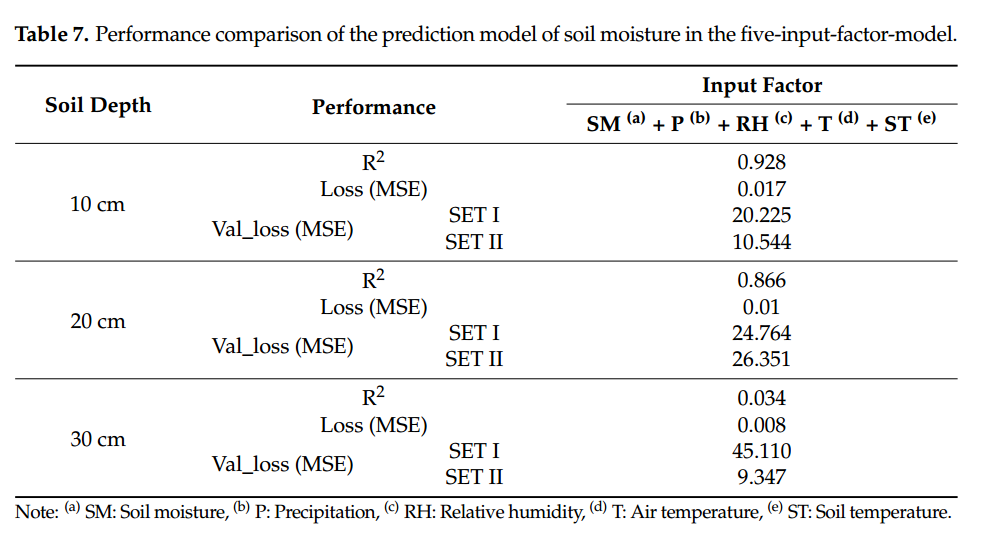
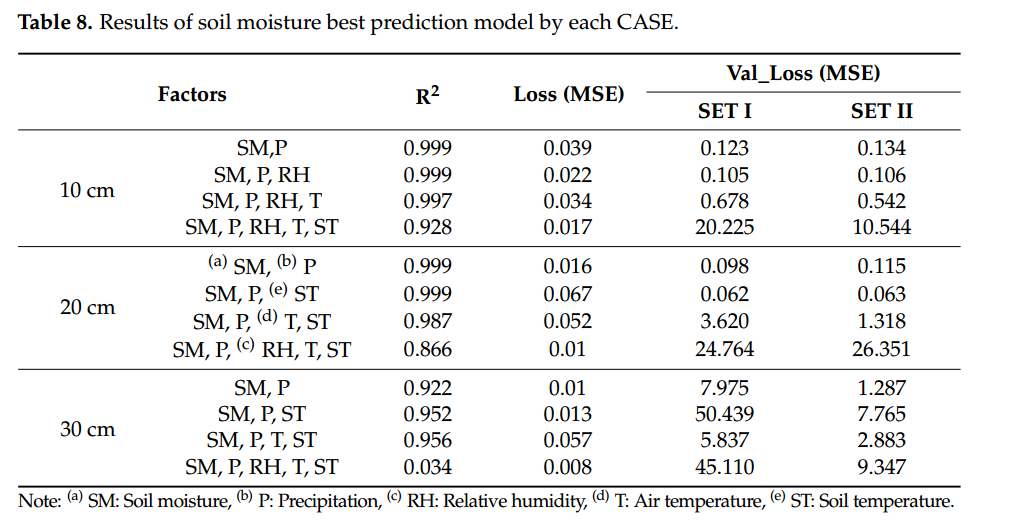
10 cm深度的最佳模型性能的R2分别为0.999、0.022和0.105,20 cm和30 cm深度的最佳模型性能的R2分别为0.999、0.016和0.098,R2分别为0.956、0.057和2.883。
RNN-LSTM模型用于确认大豆耕地的SM可预测性，并可用于供应作物生长所需的适当水分。
研究结果表明，基于时间序列天气数据的土壤水分预测模型可以帮助确定作物种植所需的适宜灌溉量。

1、介绍

递归神经网络(RNN)在处理时序数据(如时间序列数据)时是非常有效的。然而，早期的神经网络由简单的算法组成，在训练过程中不断遇到梯度消失等问题;这导致RNNs缺乏实用性的长序列。为此，提出了长短时记忆方法(LSTM)来解决长序列的消失梯度问题。为了解决斜坡的拥塞和消光问题，LSTM增加了一个步骤，决定移动到下一个时间点时是否传递隐含层处理过的结果值;即通过每个栅极打开或关闭输入和输出，通过解决斜坡拥挤和消光问题来补充长期依赖关系。
最近，利用LSTM方法预测土壤温度和水分的研究结果表明，提高土壤湿度预测性能是可能的。然而，为了提高含水率预测模型的性能，需要选择预测因子;此外，土壤湿度还受降水、前期土壤湿度、温度、湿度等因素的影响。
因此，本研究的目的是开发一个循环深度学习模型，利用SM的时间序列模式和气象数据预测大豆种植预测点之前的未来SM。特别是，利用发布的天气数据(温度、相对湿度和降水)和耕作环境的当前土壤温度和水分数据，确定了预测未来土壤深度(10 cm、20 cm和30 cm)的最佳因子。最后，建立了基于环境因子的各土层深度SM预测模型。

2、方法

2.1 数据获取

获取2020年7月5日至2020年10月4日（即大豆收获前一段时间）的土壤数据（SM，土壤温度）和天气数据（温度、湿度和降水量）。安装在耕地中心（5 m × 5 m）的传感器收集约 1 m 范围内的 SM 和土壤温度（ST）数据。
该传感器使用 TDR 型土壤传感器（SDI-12，Sentek Drill & Drop Probes，Stepney，澳大利亚）。土壤传感器的详细信息如表1所示。大豆植物的根主要分布在距表土0-30 cm的深度，深度超过30 cm时根的数量迅速减少[25]。因此，安装的土壤传感器在距全罗北道完州郡伊西面大豆种植田 10、20 和 30 厘米各深度处每隔 10 分钟测量 SM 和温度。对田间土壤性状进行调查，平均沙、粉、粘土含量分别为36.84%、35.56%、27.60%。根据美国农业部土壤分类，该土壤被分类为粘壤土。黏壤土约占韩国田间土壤总量的42%，根据研究，它是因土壤变化对大豆产量增加影响最大的土壤[26]。为了使用最少的传感器来预测未来的 SM，本研究利用了公开的环境数据。气温（T）、相对湿度（RH）和降水量（P）天气数据取自农村发展管理局农业气象信息服务发布的数据。这些天气数据是由韩国政府提供的数据自动测量的，准确度超过97.0%。获得的天气数据包括T、RH和P，它们的值是每隔10分钟测量一次的（图1）。

表1 澳大利亚 Sentek Drill & Drop Probes 土壤传感器 SDI-12 的描述

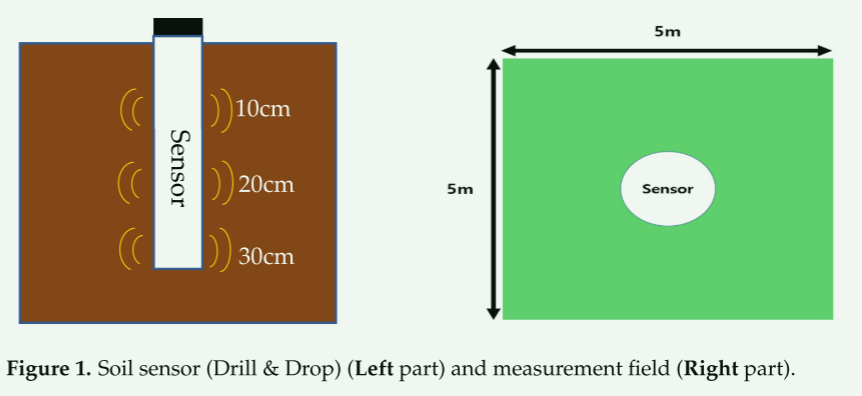
图1.土壤传感器(钻探和滴灌)(左侧)和测量区域(右侧)。

2.2.用于预测土壤湿度的 LSTM 模型

LSTM是RNN模型的一种。RNN结构基本上由三层(输入、隐藏和输出)组成，隐藏层与之前的数据相连。然而，RNN的隐含层存在长期依赖问题，当前数据中只反映了以前的值，而过去数据的?值随着时间的推移而减少；因此，它不能在长序列中实际应用。为了解决长期依赖问题，在现有的RNN中创建了三个门(输入、忘记和输出)，并通过它们传递旧信息[17]。LSTM结构如图2所示，该单元输出当前时间点的输出值yt，使用当前时间点的输入值xt输出当前时间点的隐藏状态ht，以及输出前一时间点的隐藏状态ht?1。输入和遗忘门存储来自过去和当前信息的必要信息，并删除不必要的信息，而输出门使用单元状态信息来确定输出信息[27]。对于依赖问题，在现有的RNN中创建了三个门(输入、忘记和输出)，旧信息通过它们传递[17]。LSTM结构如图2所示，该单元输出当前时间点的输出值yt，使用当前时间点的输入值xt输出当前时间点的隐藏状态ht，以及输出前一时间点的隐藏状态ht?1。输入和忘记门存储来自过去和当前信息的必要信息，并删除不必要的信息，而输出门使用单元状态信息来确定输出信息[27]

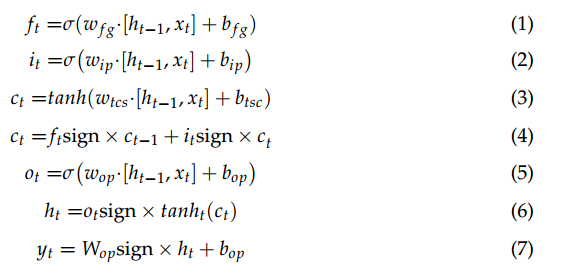
其中 ft 是被遗忘的信息； Wfg为重量； bfg 是偏差； ht?1 是上一层的输出值； xt为当前层的输入值； s 决定遗忘门中丢弃的信息量； s函数的取值范围为(0, 1)；是输入信息； wip、bip 是输入门的权重和偏置； wtcs、btsc是临时细胞状态的权重和偏差，分别是上一层和当前层的输出值； tanh函数的范围是(?1, 1)； ct 是临时单元状态 wop，bop 是输出门的权重和偏置；和 ot 由函数控制。

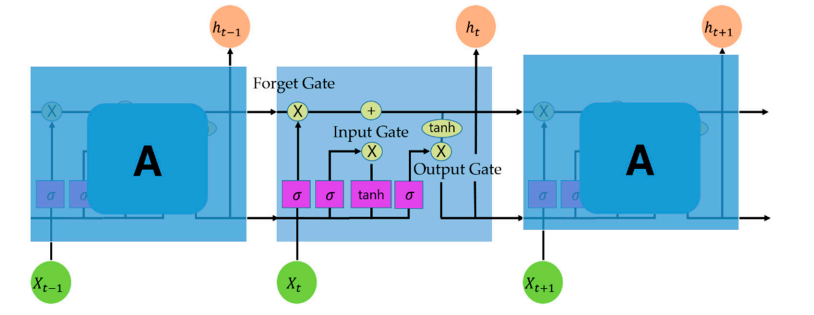
图 2. LSTM 结构

遗忘门通过将先前的隐藏状态值 ht?1 和当前的输入值 xt 输入到 sigmoid 函数（方程（1））来确定宝贵的 ct?1 存储状态。输入门是前一层和当前层的组合；即，将之前的隐藏状态值和新的输入值输入到sigmoid(方程(2))和(方程(3))以确定期望存储的新输入值。

Ct方程表示由先前的细胞状态、遗忘信息和临时细胞状态计算出的细胞状态的值。 ct 将前一个状态值 (ct?1) 乘以遗忘门，通过将前一个状态值的持有度值乘以输入门和新输入的向量值来确定当前状态的 ct（等式（ 4））。这是结合历史数据和当前数据的实现，这是 LSTM 模型的关键特征（方程（3）和（4））。输出门通过前一个隐藏状态值和新输入值的sigmoid化来确定输出值（等式（5）），将输出门的值 (ot) 与当前 ct 的 tanh 值相乘（等式（6））。
综上所述，遗忘门可以通过确定应该忘记多少先前存储单元值的逻辑来减少长期依赖问题。输入门和输出门分别确定新输入值和输出值的大小。最终值yt是通过使用输出权重和输出偏置获得的（等式（7））。

2.3.土壤水分预测的RNN-LSTM模型的建立条件

SM预测模型是使用基于TensorFlow(即，Python库)的RNN-LSTM，使用从之前1小时到现在的10分钟间隔数据来预测10分钟之后的SM的算法。MinMaxScaler被用作输入预测模型的数据的数据预处理方法，因为它可以克服仿真环境中软件误差数据在0到1的范围内的缩放(方程式(8))。标准激活函数几乎处处是压缩的，在较大值处的梯度几乎为零。这就是所谓的消失梯度问题。为了解决这个问题，引入了限制校正的线性单位(REU)[28]。Glorot等人。[29]结果表明，在隐含层使用REU激活函数，提高了各种深度神经网络的学习速度。由于RELU激活函数不存在消失梯度问题，也不涉及很大的计算代价，因此在本研究中使用它作为优化器(方程式(9))。

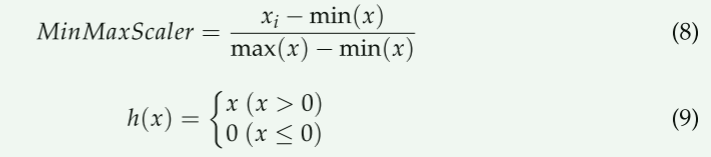
其中，xi是第i个数据，min(X)是数据最小值，max(X)是数据最大值；h(X)是函数结果，x是数据值。
深度学习的一个重要因素是学习的次数(即时代)。如果历元数较少，则学习可能不足；如果历元数较大，则可能发生过?测试。因此，需要适当数量的纪元。在本研究中，在每个环境中进行了100到20,000次的分析，以防止?过多，并根据历元的数量控制损失值的变化。?。对于损失值，在1,000到1,500次之间发生过?设置，并且通过使用当损失值没有改善时可以结束学习的早期停止功能来终止学习(如果没有改善1,000倍或更多)。

2.4.预测土壤水分的RNN-LSTM模型输入因子

以前有报道称，通过适当选择模型的输入变量可以提高SM预测的精度[30，31]。选择输入变量来预测大豆栽培中的SM是影响模型性能的重要因素。作物生长的环境因子，如T、RH、P、ST和当前土壤水分(C-SM)被用作输入变量，因为它们影响未来土壤水分(F-SM)的变化。T影响土壤水分减少，P影响土壤水分增加，RH和当前SM影响土壤水分损失和增加。因此，T、RH、P(由农业气象局获取)、ST和SM(由土壤传感器获取)被作为输入变量来寻找预测未来土壤水分(F-SM)的最佳因子。
表2显示了几个因素的组合，如T、RH、P和ST；当前土壤湿度是使用土壤深度(10厘米、20厘米和30厘米)寻找最佳因素和组合的分析方法的基本因素。

2.5.土壤水分预测的RNN-LSTM模型开发及性能检验

对于分析和预测，56%的数据(13,602个值)(从2020年7月5日0：00到2020年8月26日10：50)用作学习数据，44%用作验证数据(6000个值)。为了验证所开发的SM预测LSTM模型的性能，将验证?集合分为两种情况。?首个集合(集合I)由6,000个数据点组成，从2020年8月26日19：30到2020年10月7日11：10。培训数据采集时间为2020年8月26日19时30分至2020年10月1日14时。因此，超出培训数据范围的数据是在2020年10月1日14时至2020年10月7日11时10分之间采集的。第二个数据集(集合II)由5152个数据点组成，时间为2020年8月26日19：30至2020年10月1日14：00。在集合II中，测试数据集中的SM的时间序列模式被包括在训练数据集中的SM的时间序列模式中。因为在8月26日19：30之前的学习数据中，SM开始低于最低SM的参考点，所以在10月1日14：00分离了Veri?数据集。
为了评估模型的预测性能，计算了模型实测值与预测值之间的均方误差(MSE)和决定系数(R2)(方程式(9)和(10))。

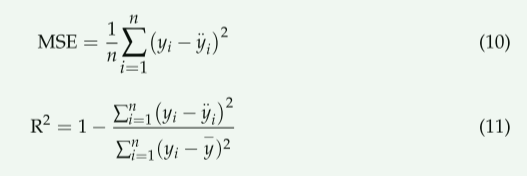
其中，yi是第i个实际值，i.Yi是第i个预测值，?y是y的平均值，n是数据点的数量。
MSE通过计算算法的损失函数来衡量预测的准确性，并通过取土壤水分实测值与深度学习模型在未来某个时间点的预测值的平方差来求平均值。R2评估算法的性能，表明在回归分析中计算出的实际值有多少；它越接近1，性能就越好。

3.成果和讨论

3.1.天气和环境数据

从栽培的100d开始，降雨47天，多云16天，晴天37天；日P在0到101.5毫米之间。大豆田土壤温度和相对湿度分别为23.72?C和82.55%。土壤水分受磷的影响较大，但反应速率因土壤深度不同而不同。

3.2.土壤水分预测的RNN-LSTM模型研究

利用天气数据（T、P 和 RH）和环境数据（SM、ST），我们开发了一个模型来预测 SM 并选择最佳因子。因此，我们通过将大豆栽培区三种不同土壤深度（10、20和30厘米）的输入变量调整为2、3、4和5来改进用于SM预测的RNN-LSTM模型

3.2.1.双输入因子模型：用于预测土壤湿度的 RNN-LSTM 模型的开发

在双输入因素模型中，使用 SM 和环境因素作为输入变量，即土壤深度为 10、20 和 30 的两个输入变量，开发了一个预测大豆种植 10 分钟后 SM 的 RNN-LSTM 模型。厘米（表 3）。当使用 SM（10、20 和 30 cm 深度）和 P 作为输入变量以及使用 SM 和 RH 作为输入变量时，训练模型经过 SETI 验证并显示出最低的验证损失值。开发 10 厘米土壤深度的 SM 预测模型的结果，当使用 SM 和 P 作为输入变量时，训练模型的准确率 R2 为 0.999，损失为 0.039。通过SETI验证，验证损失得到最好的结果，等于0.123。 R2、损失和验证损失 (SET I) 在 20 cm 深度处分别等于 0.999、0.016 和 0.098，在 30 cm 深度处分别等于 0.922、0.01 和 7.975。 SM在20cm深度时准确率最高，在30cm深度时预测准确率趋于较低。与后来的模型一样，当预测30厘米深度的SM时，表明预测了包含学习数据的SM。然而，当 SM 低于该水平时，预测性能就会下降。在学习模型的过程中，没有出现SM不低于32.7%的情况。因此，低于该值的预测，判断为难以跟上趋势。 SET II验证的结果与SET I相似；当SM和P作为输入变量，深度为10 cm时，验证损失为0.1344；当深度为 20 cm 的 SM 时，验证损失为 0.1147；当深度为 30 cm 的 SM 和 P 作为输入变量时，验证损失为 1.2867。
表3 土壤湿度预测模型在双输入因子下的性能比较

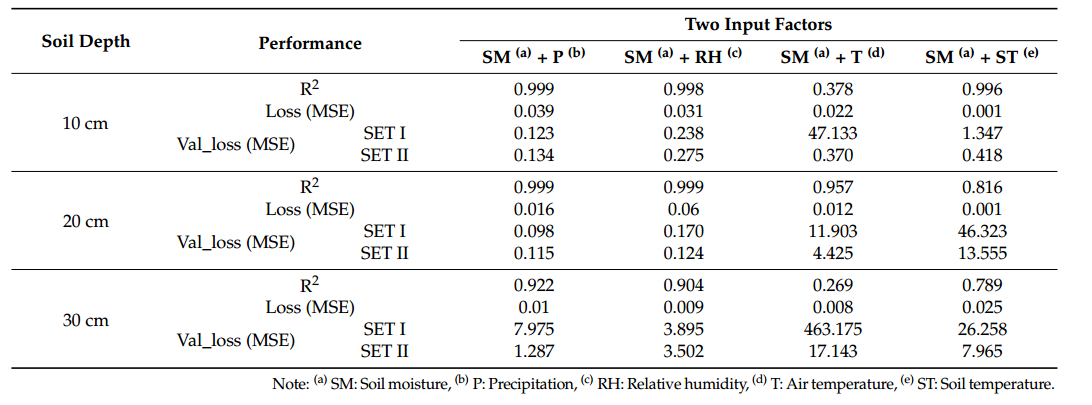
比较每组结果，当使用两个因子预测 SM 时，选择 SM 和 P 作为每个深度（10、20 和 30 cm）的最佳因子，似乎比 RH 更受 P 的影响，因为 P与土壤湿度有直接关系。接下来，发现RH受到影响。包含 RH 和 SM 作为因子的训练模型在 10 cm 深度的结果为：R2 为 0.998，损失为 0.031，SET I 验证损失为 0.238，SET II 验证损失为 0.275。在20 cm和30 cm深度处，训练模型的R2、损失、损失SET I的验证损失和SET II的验证损失分别为0.999、0.06、0.170和0.124以及0.904、0.009、3.895和3.502 。在20 cm和30 cm深度验证情况下，带降水因子的模型表现优于带相对湿度因子的模型。 RH 之后，准确度按照 ST 和 T 的顺序提高。因此，对于使用两个因子预测 SM，选择 SM 和 P 作为最佳因子。接下来，选择SM和RH。图 4 显示了在两个输入因子中每个深度具有最佳性能的预测模型。图 4-7 是显示从中午 12 点开始测量的 13,604 个时间序列数据的图表。 2020年7月5日至2020年10月7日上午11点10分，从晚上7点30分开始预测6000个时间序列结果2020年8月26日至2020年10月7日上午11点10分。在同时使用SM和P的预测模型的情况下，如图4a所示，20深度土壤湿度保持在15%左右的原因cm且在30cm深度处小于32%是训练模型不包含显示时间序列特征的数据；因此，预测误差较大。

3.2.2.三输入因素模型：用于预测土壤湿度的 RNN-LSTM 模型的开发

在三输入因子模型中，使用两个输入因子选择的 SET I 期间的两个最佳因子，根据土壤深度（10 cm、20 cm 和 30 cm）开发了用于预测大豆种植 SM 的 RNN-LSTM 模型以及其余环境因素之一作为输入变量。
表4 土壤湿度预测模型在三输入因子I下的性能比较

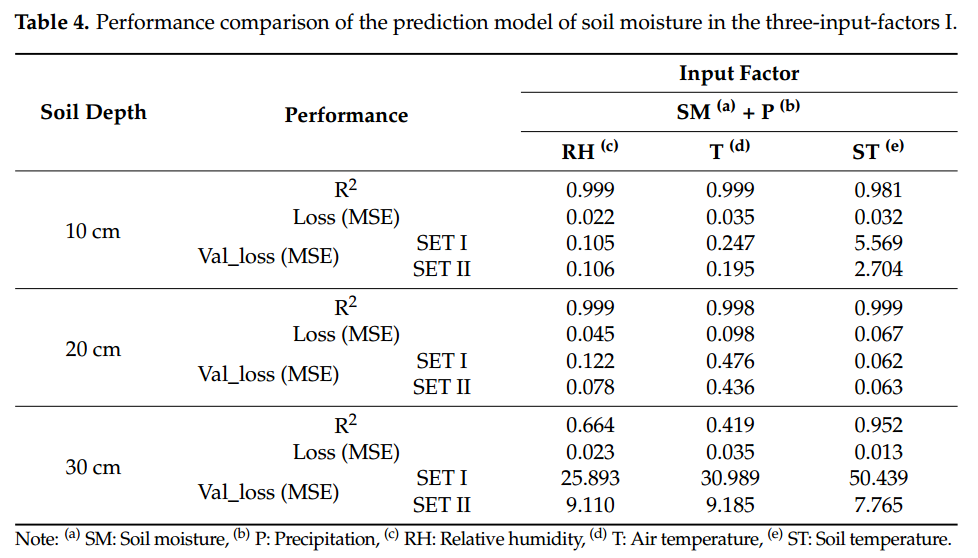
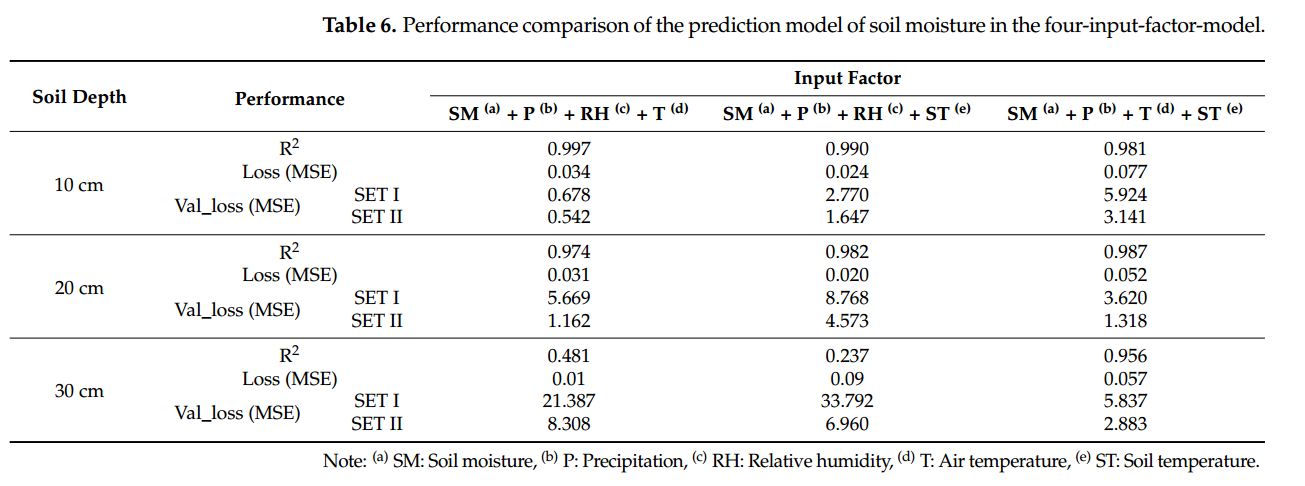
4、结论

在这项研究中，建立了预测大豆种植地未来SM的RNN-LSTM模型，该模型利用SM的时间序列模式和直到预报点的天气数据。首先，我们选择了最优的栽培环境变量来预测大豆种植时的SM，并建立了由土层深度预测SM的RNN-LSTM模型。为了提高SM的预测性能，建立了每个深度组合的预测模型，并用包含学习范围外的数据的集合I和不包含数据的集合II进行了验证。Set I?检验结果显示，SM、P和RH(R2=0.999，损失0.022，验证损失0.105)选择在10 cm深度；SM、P和ST(R2=0.999，损失0.067，验证损失0.062)选择在深度20 cm；SM、P、T和ST(R2=0.956，损失0.057，验证损失5.837)选择在30 cm深度。SET II验证表明，SM和P(R2=0.922，损失0.01，验证损失1.287)是30 cm深度的最佳选择。研究了基于时间序列SM数据的RNN-LSTM在不同学习数据条件下的最优因子特征。通过本研究，利用RNN-LSTM模型验证了大豆耕地SM的可预测性，并可用于预测作物生长所需的水分供应。通过对未来土壤水分的预测，它可以帮助制定作物栽培所需的决策，如是否灌溉。未来还将进行进一步的研究，通过增加数据采集周期和大小来提高预测性能。