数据结构二（C语言）

哈希表

哈希函数的两个问题：
（1）哈希函数，让键值尽量平均分布
（2）解决冲突，拉链法

哈希表结构

哈希表的基本操作
get(k key)，根据键获取对应的值,int index = hash(key);
遍历链表；key存在，返回key对应的value；key不存在，返回特殊值
put(k key,v value),添加键值对，如果键值对已经存在，更新键值对的值，int index = hash(key);
遍历链表：key存在，更新key对应的value，并返回原来的value；kay不存在，添加键值对，返回特殊值
remove(k key),删除键值对，int index = hash(key);
遍历链表：key存在，删除键值对，并返回对应的值；key不存，返回特殊值

#include <stdlib.h>
#include <stdio.h>
#define N 2043

typedef char * K;
typedef  int V;
typedef struct entry_s{
	K key;
	V val;
	struct entry_s* next;
} Entry; 
typedef struct {
	Entry* table[N];
} HashMap;

//创建空的哈希表
HashMap* HashMap_create() {
	return (HashMap*)calloc(1,sizeof(HashMap));
}

//哈希函数
int hash(char* key) {
	int h = 0,g;
	while(*key) {
		h = (h << 4) + *key++;
		g = h & 0xf0000000;
		if(g)
			h^= g >> 24;
		h &= ~g;
	}
	return h % N;
}

void HasgMapo_destroy(HashMap* map) {
	//释放所有节点
	for (int i = 0;i < N;i++) {
		Entry*curr = map->table[i];
		while(curr != NULL) {
			//保存后继节点
			Entry* next = curr->next;
			free(curr);
			curr = next;
		}
	}
	//释放HashMap结构体
	free(map);
}


V HansshMap_get(HashMap* map,K key) {
	//根据key获取索引
	 int idx = hash(key);
	 //遍历链表
	 Entry* curr = map->table[idx];
	 while(curr != NULL) {
	 	//判断key是否存在
	 	if(strcmp(key,curr->key) == 0) {
	 		return curr->val;
	 	}
	 	curr = curr->next;
	 }
	 //不存在这样的key
	 return -1;
}

V HashMap_put(HashMap* map,K key,V val) {
	//根据key获取索引
	 int idx = hash(key);
	 //遍历链表
	 Entry* curr = map->table[idx];
	 while(curr != NULL) {
	 	//判断key是否存在
	 	if(strcmp(key,curr->key) == 0) {
	 		V oldValue = curr->val;
	 		curr->val = val;
	 		return oldValue;
	 	}
	 	curr = curr->next;
	 }
	 //不存在这样的key,添加节点，头插法
	 //创建键值对
	 Entry* entry = (Entry*)malloc(sizeof(Entry));
	 if(entry == NULL) {
	 	printf("Error:malloc failed in HashMap_put.\n");
	 	exit(1);
	 }
	 entry->key = key;
	 entry->val = val;
	 entry->next = nmao->table[idx];
	 //更新链表的头节点
	 map->table[idx] = entry;
	 return -1;
}

V HsahMap_remove(HashMap* map,K key) {
	//根据key获取索引
	 int idx = hash(key);
	 //遍历链表
	 Entry* prev = NULL;
	 Entry* curr = map->table[idx];
	 while(curr != NULL) {
	 	//判断key是否存在
	 	if(strcmp(key,curr->key) == 0) {
	 		//删除节点
	 		if(prev == NULL) {
	 			map->table[idx] = curr->next;
	 		}else {
	 			prev->next = ccurr->next;
	 		}
	 		//释放空间
	 		V removeValue = currr->val;
	 		free(curr);
	 		return removeValue;
	 	}
	 	curr = curr->next;
	 }
	 //不存在这样的key
	 return -1;
}

二叉搜索树（BST）

二叉树的遍历：
（1）深度优先遍历【前序遍历，中序遍历，后序遍历】
（2）广度优先遍历（层级遍历）

二叉查找树（Binary Search Tree）

1.二叉树
2.左子树所有结点的key值都小于根结点多的key值
右子树所有结点的key值都大于根结点的key值
并且左、右子树都是二叉查找树

查看中序遍历序列可以判定一颗二叉树是不是二叉查找树（BST），如果中序遍历序列是递增的那么是二叉查找树

二叉查找树的好处：方便查找，相当于二分查找，
查找效率：O(h),h为树的高度
插入的效率：O(h)
删除的效率：O(h)

如果一颗BST有N个结点，那么他最小的高度是完全二叉树的最小高度

平衡二叉查找树（AVL）:对任意一个结点，它的左子树的告诉和右子树的高度相差不超过1
红黑树：广义上来来说也是一颗平衡二叉树，保证树的高度是O(logn)级别

2-3-4树

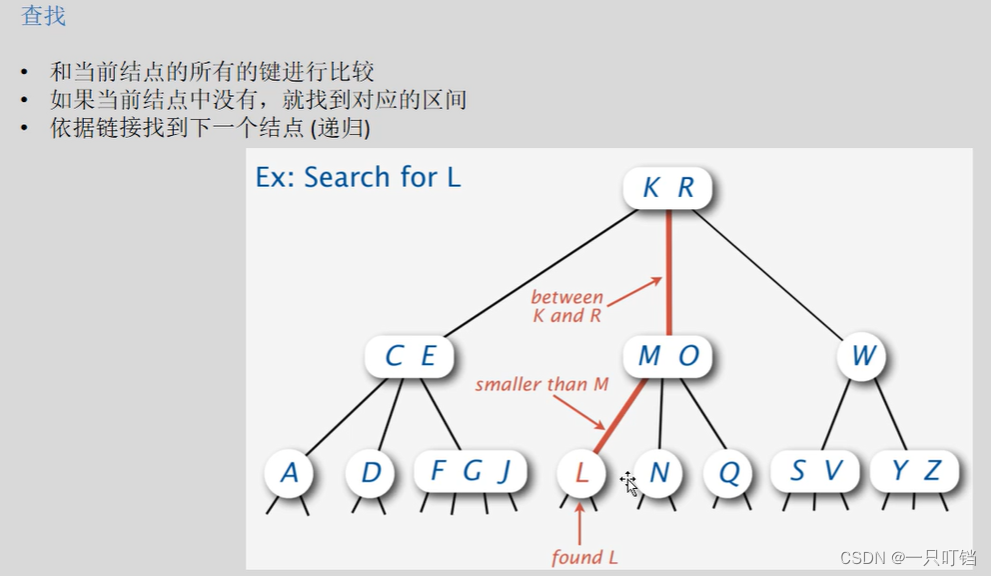
红黑树就是一种比较简单2-3-4树实现方式

红黑树是一个二叉查找树（BST），我们就是使用二叉查找树来表示2-3-4树

#include <stdbool.h>
#include <stdio.h>
#include  <string.h>

#define RED false
#define BLACK true

typedef char T;

typedef struct TreeNode_s {
	bool color;
	T key;
	struct TreeNode_s* left;
	struct TreeNode_s* right;
	struct TreeNode_s* parent;
}TreeNode;

typedef struct {
	TreeNode* root;
}RBTree;

//红黑树树的遍历
//先序遍历
void RBTree_preOrder(RBTree* tree) {
	//委托这个方法实现
	preOrder(tree->root);
}
void preOrder(TreeNode* root) { 
	//边界条件
	if(root == NULL) return ;
	//遍历根结点
	printf("%c ",root->key);
	//遍历左子树
	inOrder(root->left);
	//遍历右子树
	inOrder(root->right);
}

//中序遍历
void RBTree_inOrder(RBTree* tree) {
	//委托这个方法实现
	inOrder(tree->root);
}
void inOrder(TreeNode* root) { 
	//边界条件
	if(root == NULL) return ;
	//遍历左子树
	inOrder(root->left);
	//遍历根结点
	printf("%c ",root->key);
	//遍历右子树
	inOrder(root->right);
}

//后序遍历
void RBTree_postOrder(RBTree* tree) {
	//委托这个方法实现
	postOrder(tree->root);
}
void postOrder(TreeNode* root) {
	//边界条件
	if(root == NULL) return;
	//遍历左子树
	postOrder(root->left);
	//遍历右子树
	postOrder(root->right);
	//遍历根结点
	printf("%c ",root->key);
}

//层次遍历/广度优先遍历(使用队列实现)
void RBTree_levelOrder(RBTree* tree) {
	if(tree->root == NULL) return ;
	Queue* q = Queue_create();
	//将根结点入队
	enqueue(q,tree->root);
	while(!isEmpty(q)) {
		//出队列
		TreeNode* node = dequeue(q);
		printf("%c ",node->key);
		if(node->left != NULL) {
			enqueue(q,node->left);
		}
		if(node->right != NULL) {
			enqueue(q,node->right);
		}
	}
}
//建树(按照树的先序、中序遍历结果构建树)
TreeNode* build(char * preOrder,char* inOrder,int len) {
	char ch = *preOrder;
	//构建根结点
	TreeNode* root = (TreeNode*)calloc(1,sizeof(TreeNode));
	root->key = ch;
	int idx = 0;
	for(;idx < len;idx++) {
		if(inOrder[idx] == ch) {
			break;
		}
	}
	//[0..idx-1]idx[idx+1,len-1]
	//构建左子树
	root->left = build(preOrder + 1,inOrder,idx); 
	//构建右子树
	root->right = build(preOrder+idx+1,inOrder+idx+1,len-idx-1);
	return root;
}
Tree* RBTree_build(char* preOrder,char* inOrder,int len) {
	RBTree* tree = (RBTree*) calloc(1,sizeod(RBTree));
	//创建所有结点，并把创建后的根结点赋值给 tree->root
	tree->root = build(preOrder,inOrder,len);
	return tree;
}