【详解：两数之和&&三数之和&&四数之和】

本文讲解两数之和，三数之和和四数之和这三道经典双指针类型题。会在详解题目的同时给出AC代码【这三个题目从前往后是循序渐进的，非常巧妙】

目录

1、查找总价格为目标值的两个商品

2、三数之和

3、力扣18. 四数之和

---

1、查找总价格为目标值的两个商品

【本题即两数之和经典例题】?

解法一：暴力解法

本题是升序的数组，因此可以用「对撞指针」优化时间复杂度。
算法流程（附带算法分析，为什么可以使用对撞指针）：
a.?初始化?left ， right 分别指向数组的左右两端（不是我们理解的指针，而是数组的下标）
b.?当?left < right 的时候，一直循环

• ?当 nums[left] + nums[right] == target 时，说明找到结果，记录结果，并且返回；
• ?当?nums[left] + nums[right] < target 时：
• ?对于?nums[left] 而言，此时?nums[right] 相当于是?nums[left] 能碰到的最大值。如果此时不符合要求，我们可以让left++，使和变大
• ?当?nums[left] + nums[right] > target 时，同理我们可以舍去nums[right] （因为和过大了，应该小一点）。让?right-- ，继续比较下一组数据，而?left 指针不变

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) {
        int left = 0, right = price.size() - 1;
        int sum = 0;
        while (left < right)
        {
            sum = price[left] + price[right];
            if (sum > target) right--;
            else if (sum < target) left++;
            else return {price[left], price[right]};//这么返回会被视为vector返回
        }
        //因为没结果也要有返回值，所以为了让编译器过，随便设置一个返回值
        return {-1, -1};
    }
};

---

2、三数之和

找三元组的过程：?

去重： 【当然也可以用set等，但是我们可以想另一个办法】

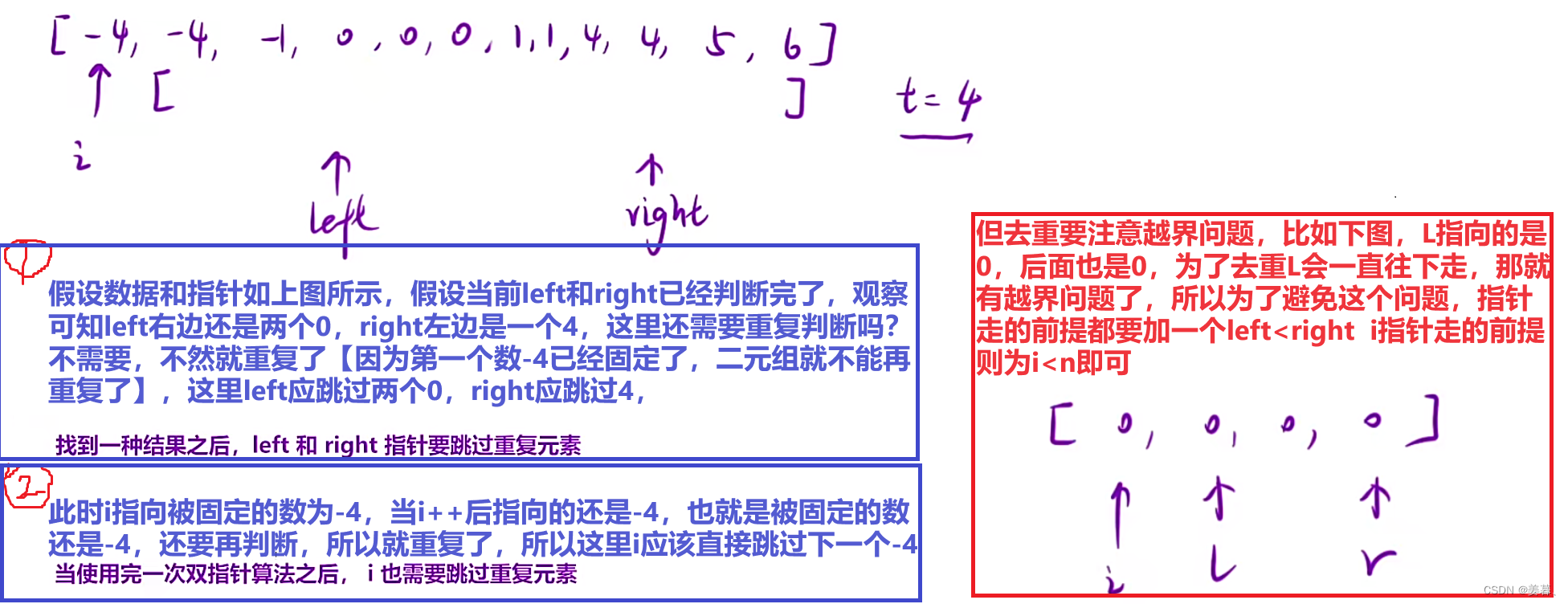
class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> ret;
        //1、排序
        sort(nums.begin(), nums.end());
        //2、双指针算法解决问题
        int  n = nums.size();
        for (int i = 0; i < n;)
        {
            if (nums[i] > 0) break;//优化：若固定的数都>0，且是升序，后面之和不可能有负数
            //沿用两数之和操作
            int left = i + 1, right = n - 1 , target = -nums[i];
            while (left < right)
            {
                int sum = nums[left] + nums[right];
                if(sum < target) left++;
                else if (sum > target) right--;
                else{
                   ret.push_back({nums[i], nums[left], nums[right]});
                   left++, right--; 
                     //对两个指针去重,前提是这个地方已经作为答案了，所以放在else中
                    while (left < right && nums[left - 1] == nums[left]) left++;
                    while (left < right && nums[right + 1] == nums[right]) right--;
                }
            }
            //对i指针去重
            i++;
            while (i < n && nums[i - 1] == nums[i]) i++;
        }
        return ret;
    }
};

---

3、力扣18. 四数之和

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> ret;
        //1、排序
        sort(nums.begin(), nums.end());

        int n = nums.size();
        //2、利用双指针思想求解
        for (int i = 0; i < n;) //固定数a
        {
            //利用三数之和思路求解
            for (int j = i + 1; j < n;) //固定数b
            {
                int left = j + 1, right = n - 1;
                //数据范围为-10亿~10亿，那三个数相+-一定超int[-21亿~21亿]
                //所以这里用long long才行，强转即可
                long long t = (long long)target - nums[i] - nums[j];
                while (left < right)
                {
                    int sum = nums[left] + nums[right];
                    if (sum > t) right--;
                    else if (sum < t) left++;
                    else 
                    {
                        ret.push_back({nums[i],nums[j],nums[left++],nums[right--]});
                        //对双指针去重
                        while (left < right && nums[left-1] == nums[left]) left++;
                        while (left < right && nums[right+1] == nums[right]) right--;
                    }
                }
                //对j指针指向的数去重
                j++;
                while (j < n && nums[j - 1] == nums[j]) j++;
            }    
            //对i指针指向的数去重
            i++;
            while (i < n && nums[i - 1] == nums[i]) i++;        
        }
        return ret;
    }
};

---