机器学习实验3——支持向量机分类鸢尾花

🧡🧡实验内容🧡🧡

基于鸢尾花数据集，完成关于支持向量机的分类模型训练、测试与评估。

🧡🧡数据预处理🧡🧡

代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# ==================特征探索====================

# ===认识数据===
iris = datasets.load_iris()
print("Feature names: {}".format(iris['feature_names']))
print("Target names: {}".format(iris["target_names"]))
print("target:\n{}".format(iris['target'])) # 0 代表setosa，1 代表versicolor，2 代表virginica。
print("shape of data: {}".format(iris['data'].shape))

# ===转为df对象===
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
feature_df=df.drop('label',axis=1,inplace=False) # 取出特征
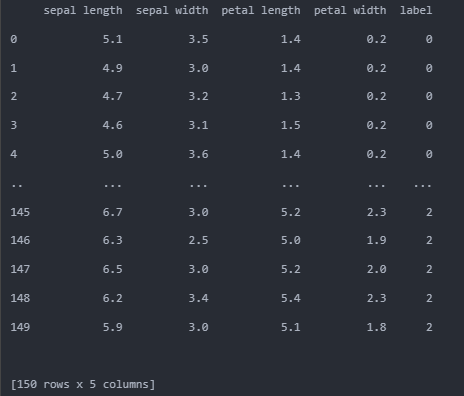
print(df)

# ===相关性矩阵===
corr_matrix = feature_df.corr()
plt.figure(figsize=(8, 6))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

# ===径向可视化===
ax = pd.plotting.radviz(df, 'label', colormap='brg')
ax.add_artist(plt.Circle((0,0), 1, color='r', fill = False))

# ===各特征之间关系矩阵图===
# 设置颜色主题
g = sns.pairplot(data=df, palette="pastel", hue= 'label')

认识数据

属性：花萼长度，花萼宽度，花瓣长度，花瓣宽度
分类：Setosa，Versicolour，Virginica

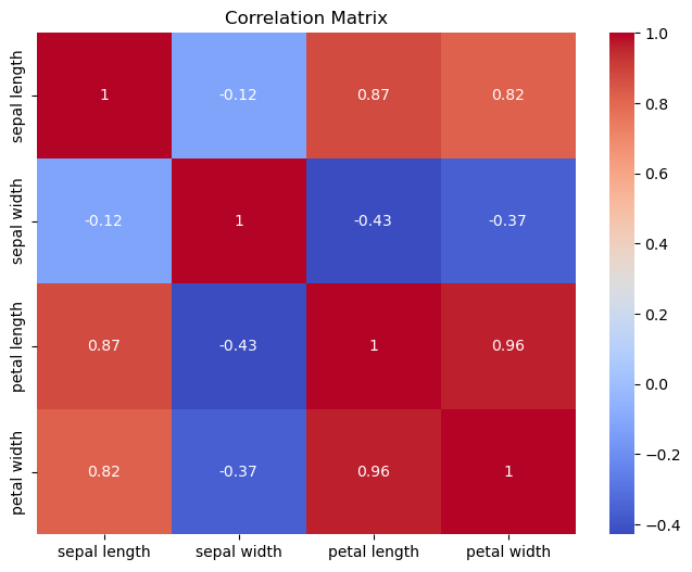
相关性分析

如下图，可以直观看到花瓣宽度（Petal Width）和花瓣长度（Petal Length）存在很高的正相关性，且它们与花萼长度（Speal Length）也具有很高的正相关性，而花萼宽度（Speal Width）与其他三个属性特征的相关性均很弱。

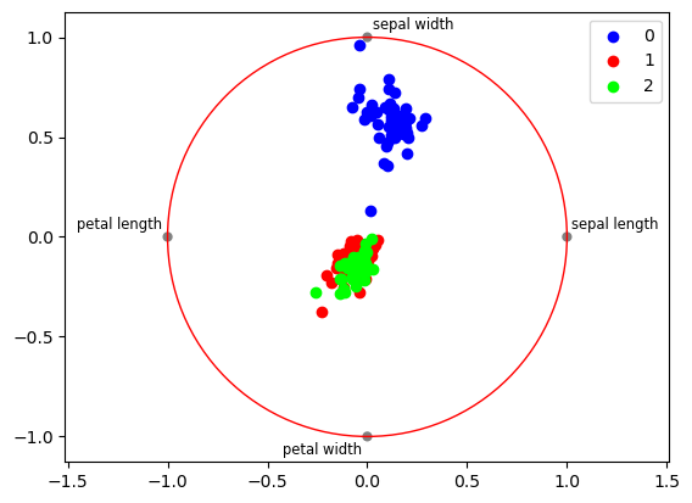
径向可视化

用于观察每种类别花的四个特征之间的相对关系（线性大小关系）。
如下图，其中0、1、2分别对应Setosa，Versicolour，Virginica类别，可以直观看出：Setosa花的花萼宽度（Speal Width）和花萼长度（Speal Length）这两个特征相比其他两个特征花瓣宽度（Petal Width）和花瓣长度（Petal Length）具有区分性，而Versicolour，Virginica花的四个特征分布很相似，不好区分。

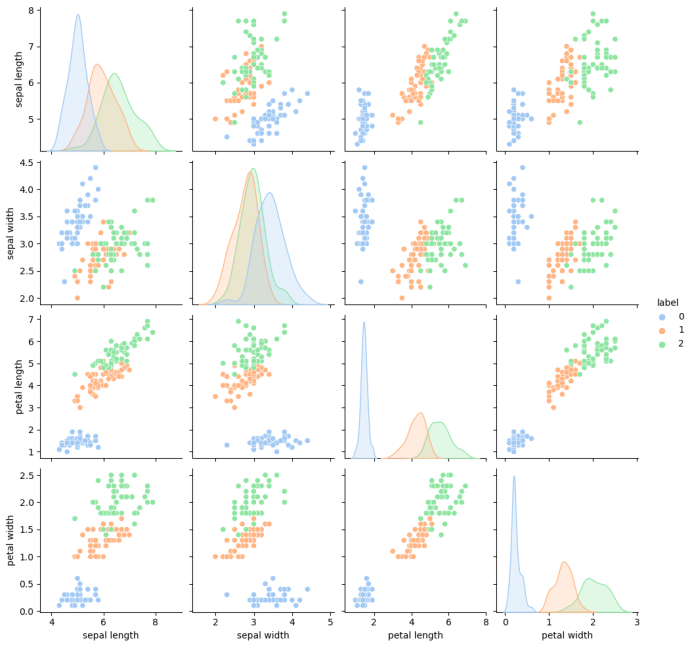
各个特征之间的关系图

从下图可以看出，Setosa花的花瓣宽度（Petal Width）和花瓣长度（Petal Length）的分布相比其他两类具有很好的区分性。

🧡🧡支持向量机SVM求解🧡🧡

直觉理解：

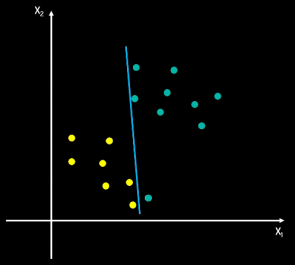
对于二维特征，如何区分图中不同的点
第一种思路：如下左图画一条线，但是是一个不太好的分割线
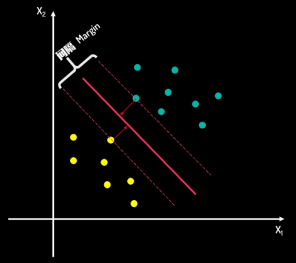
而换一种思路，如下右图，先找两个分类的决策边界(两边的虚线)之间的间隔区域，再取间隔区域的中间为分割线，这样能保证分割效果最佳。因此寻找最佳决策边界线（中间线）的问题可以转化为求解两类数据的最大间隔问题。

因此将决策边界上下移动c，得到间隔的两个边界线，如下左图，此时这两个边界线称为支持向量，它们决定了间隔距离。如下右图，经过数学变换，可以得到最终要求的超平面表达式，即求解参数w、b即可

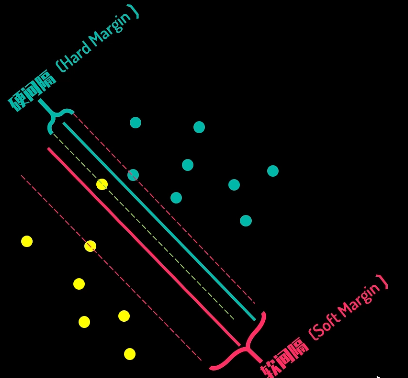
除此之外，只考虑分类点的决策边界之间的距离的间隔，称为硬间隔，同时考虑距离和异常点损失（下图红线上方的黄点）的间隔，称为软间隔。

数学推导

某点到超平面的距离r：（几何间隔，可以代表分类正确的确信度）

目标超平面之间的间隔距离γ：

约束条件：点到超平面距离r >= 超平面间隔距离γ的一半：

则最终求解的函数表达式为：

但是以上函数表达式为非凸函数，因此要：

1. 先转为凸函数
2. 用拉格朗日乘子法和KKT条件求解对偶问题

1.转为凸函数：

2.用拉格朗日乘子法和KKT条件求解对偶问题
这个过程就涉及到高阶的数学知识了，我这里也不是很懂，只大概了解：
为什么要用拉格朗日乘子法：将不等式约束转换为等式约束。
整合成如下拉格朗日表达式：

依据对偶性，求解问题为：

先求解：
根据KKT条件：对w、b求偏导可得：

代入L(w,b,a)：
再求解：

3.利用SMO求解α、从而求解w、b
现在优化问题变成了如上的形式，但是它的规模正比于训练样本数m，当m很大时，会有很大开销，因此针对这个问题的特性，有更高效的优化算法，即序列最小优化（SMO）算法。
其大概思想是：先固定α以外的参数，然后对α求极值，在上述约束条件下，α可以由其他变量导出，这样，在参数初始化后，不断迭代，可以最终达到收敛。
通过SMO求得的w、b为：

则超平面的公式为：

最后根据超平面的符号，表达成分类决策函数即可：

代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler


class SMO:
    def __init__(self, X, y, C, kernel, tol, max_passes=10):
        self.X = X  # 样本特征 m*n m个样本 n个特征
        self.y = y  # 样本标签 m*1
        self.C = C  # 惩罚因子, 用于控制松弛变量的影响
        self.kernel = kernel  # 核函数
        self.tol = tol  # 容忍度
        self.max_passes = max_passes  # 最大迭代次数
        self.m, self.n = X.shape
        self.alpha = np.zeros(self.m)
        self.b = 0
        self.w = np.zeros(self.n)

    # 计算核函数
    def K(self, i, j):
        if self.kernel == 'linear':
            return np.dot(self.X[i].T, self.X[j])
        elif self.kernel == 'rbf':
            gamma = 0.5
            return np.exp(-gamma * np.linalg.norm(self.X[i] - self.X[j]) ** 2)

        else:
            raise ValueError('Invalid kernel specified')

    def predict(self, X_test):
        pred = np.zeros_like(X_test[:, 0])
        pred = np.dot(X_test, self.w) + self.b
        return np.sign(pred)

    def train(self):
        """
        训练模型
        :return:
        """
        passes = 0
        while passes < self.max_passes:
            num_changed_alphas = 0
            for i in range(self.m):
                # 计算E_i, E_i = f(x_i) - y_i, f(x_i) = w^T * x_i + b
                # 计算误差E_i
                E_i = 0
                for ii in range(self.m):
                    E_i += self.alpha[ii] * self.y[ii] * self.K(ii, i)
                E_i += self.b - self.y[i]
                # 检验样本x_i是否满足KKT条件
                if (self.y[i] * E_i < -self.tol and self.alpha[i] < self.C) or (self.y[i] * E_i > self.tol and self.alpha[i] > 0):
                    # 随机选择样本x_j
                    j = np.random.choice(list(range(i)) + list(range(i + 1, self.m)), size=1)[0]
                    # 计算E_j, E_j = f(x_j) - y_j, f(x_j) = w^T * x_j + b
                    # E_j用于检验样本x_j是否满足KKT条件
                    E_j = 0
                    for jj in range(self.m):
                        E_j += self.alpha[jj] * self.y[jj] * self.K(jj, j)
                    E_j += self.b - self.y[j]

                    alpha_i_old = self.alpha[i].copy()
                    alpha_j_old = self.alpha[j].copy()

                    # L和H用于将alpha[j]调整到[0, C]之间
                    if self.y[i] != self.y[j]:
                        L = max(0, self.alpha[j] - self.alpha[i])
                        H = min(self.C, self.C + self.alpha[j] - self.alpha[i])
                    else:
                        L = max(0, self.alpha[i] + self.alpha[j] - self.C)
                        H = min(self.C, self.alpha[i] + self.alpha[j])

                    # 如果L == H，则不需要更新alpha[j]
                    if L == H:
                        continue

                    # eta: alpha[j]的最优修改量
                    eta = 2 * self.K(i, j) - self.K(i, i) - self.K(j, j)
                    # 如果eta >= 0, 则不需要更新alpha[j]
                    if eta >= 0:
                        continue

                    # 更新alpha[j]
                    self.alpha[j] -= (self.y[j] * (E_i - E_j)) / eta
                    # 根据取值范围修剪alpha[j]
                    self.alpha[j] = np.clip(self.alpha[j], L, H)

                    # 检查alpha[j]是否只有轻微改变，如果是则退出for循环
                    if abs(self.alpha[j] - alpha_j_old) < 1e-5:
                        continue

                    # 更新alpha[i]
                    self.alpha[i] += self.y[i] * self.y[j] * (alpha_j_old - self.alpha[j])

                    # 更新b1和b2
                    b1 = self.b - E_i - self.y[i] * (self.alpha[i] - alpha_i_old) * self.K(i, i) \
                         - self.y[j] * (self.alpha[j] - alpha_j_old) * self.K(i, j)
                    b2 = self.b - E_j - self.y[i] * (self.alpha[i] - alpha_i_old) * self.K(i, j) \
                         - self.y[j] * (self.alpha[j] - alpha_j_old) * self.K(j, j)

                    # 根据b1和b2更新b
                    if 0 < self.alpha[i] and self.alpha[i] < self.C:
                        self.b = b1
                    elif 0 < self.alpha[j] and self.alpha[j] < self.C:
                        self.b = b2
                    else:
                        self.b = (b1 + b2) / 2

                    num_changed_alphas += 1

            if num_changed_alphas == 0:
                passes += 1
            else:
                passes = 0

        # 提取支持向量和对应的参数
        idx = self.alpha > 0  # 支持向量的索引
        # SVs = X[idx]
        selected_idx = np.where(idx)[0]
        SVs = self.X[selected_idx]
        SV_labels = self.y[selected_idx]
        SV_alphas = self.alpha[selected_idx]

        # 计算权重向量和截距
        self.w = np.sum(SV_alphas[:, None] * SV_labels[:, None] * SVs, axis=0)
        self.b = np.mean(SV_labels - np.dot(SVs, self.w))
        print("w", self.w)
        print("b", self.b)

    def score(self, X, y):
        predict = self.predict(X)
        print("predict", predict)
        print("target", y)
        return np.mean(predict == y)
        
# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target
y[y != 0] = -1
y[y == 0] = 1 # 分成两类



# 为了方便可视化，只取前两个特征
X2 = X[:,:2]
# # 分别画出类别 0 和 1 的点
plt.scatter(X2[y == 1, 0], X2[y == 1, 1], color='red',label="class 1")
plt.scatter(X2[y == -1, 0], X2[y == -1, 1], color='blue',label="class -1")
plt.xlabel("Speal Width")
plt.ylabel("Speal Length")
plt.legend()
plt.show()

# 数据预处理，将特征进行标准化，并将数据划分为训练集和测试集
scaler = StandardScaler()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=3706)
X_train_std = scaler.fit_transform(X_train)

# 创建SVM对象并训练模型
svm = SMO(X_train_std, y_train, C=0.6, kernel='rbf', tol=0.001)
svm.train()


# 预测测试集的结果并计算准确率
X_test_std = scaler.transform(X_test)
accuracy = svm.score(X_test_std, y_test)
print('正确率: {:.2%}'.format(accuracy))

from sklearn.metrics import confusion_matrix, roc_curve, auc
y_pred=svm.predict(X_test_std)

# 绘制混淆矩阵
def cal_ConfusialMatrix(y_true_labels, y_pred_labels):
    cm = np.zeros((2, 2))
    y_true_labels = [0 if x == -1 else x for x in y_true_labels]
    y_pred_labels = [0 if x == -1 else x for x in y_pred_labels]
    for i in range(len(y_true_labels)):
        cm[ y_true_labels[i], y_pred_labels[i] ] += 1
    plt.figure(figsize=(8, 6))
    sns.heatmap(cm, annot=True, fmt='g', cmap='Blues', xticklabels=['Predicted Negative', 'Predicted Positive'], yticklabels=['Actual Negative', 'Actual Positive'])
    plt.xlabel('Predicted label')
    plt.ylabel('True label')
    plt.title('Confusion Matrix')
    plt.show()

y_pred=[int(x) for x in y_pred]
y_test=[int(x) for x in y_test]
cal_ConfusialMatrix(y_test, y_pred)

运行结果

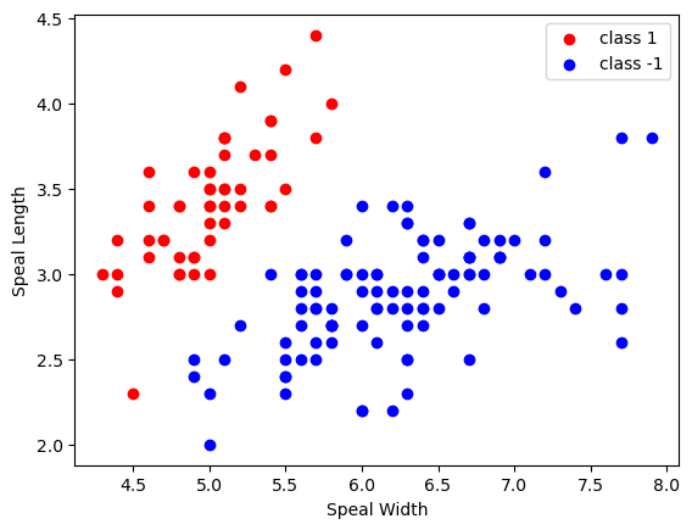
由于鸢尾花为三分类，为了简化实验，这里先把setosa定义为1类（+1），versicolor、virginica组合定义为1类（-1）。
做出其对于sepal width和sepal length的分布图，可以看到，训练样本应该是线性可分的。

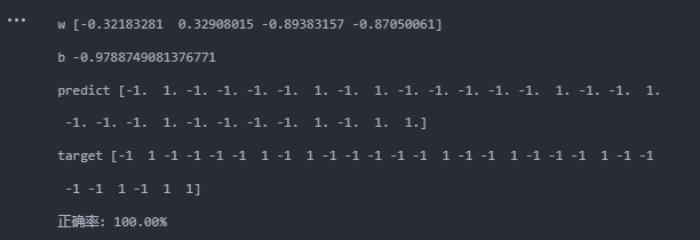
按照训练集：测试集=8：2的比例进行训练，之后进行测试集分类结果如下：

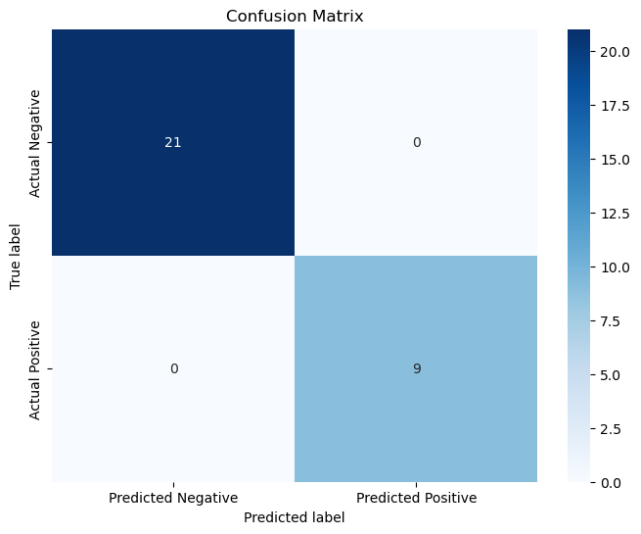
线性核：

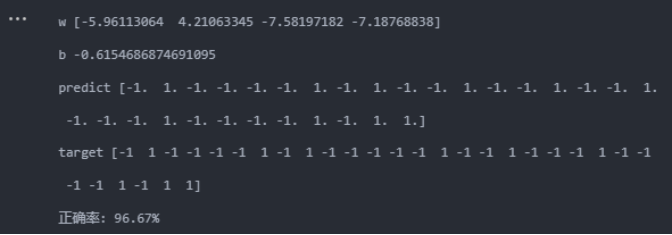
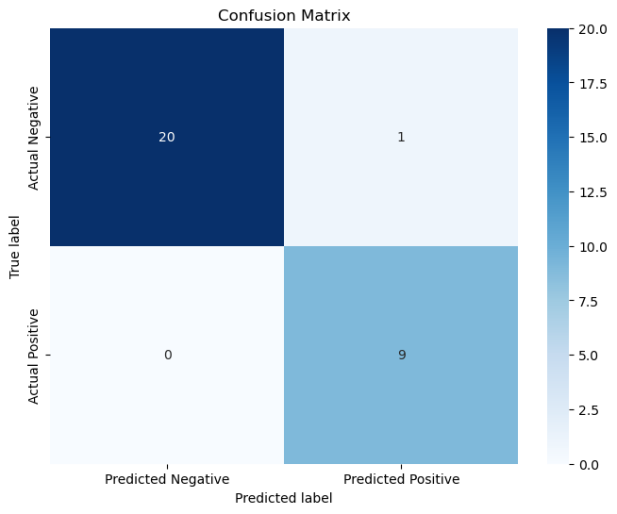
高斯核：

🧡🧡总结🧡🧡

实验结果：
当使用的核函数为线性核时，准确率能达到100%，而使用高斯核时，准确率降低到96.67%（其实从混淆矩阵可以看到，只分类错误1个），且运行时间相对长很多。

分析原因：
线性核适用于数据集具有线性可分性的情况，即类别之间可以通过一条直线进行划分。在这种情况下，线性核可以提供较好的分类性能，并且计算效率较高。
高斯核可以更好地处理非线性问题。高斯核可以将输入空间映射到一个更高维度的特征空间，从而使得数据在新的特征空间中更容易被线性分割。但是，高斯核也有其缺点：在使用高斯核时，需要调整的超参数较多，如 gamma 参数和正则化参数 C，不正确的参数选择可能导致过拟合或欠拟合的问题。此外，高斯核计算复杂度较高，需要计算每个样本与其他样本之间的相似度，因此在数据集上的训练和预测时间可能较长。
因此综合分析，本实验中鸢尾花的特征为线性，因此使用线性核效果更佳。同时高斯核对参数比较敏感，实验中对于高斯核的参数选择可能也不够恰当。