DropBlock（NeurIPS 2018）论文与代码解析

paper：DropBlock: A regularization method for convolutional networks

third-party implementation：https://github.com/open-mmlab/mmdetection/blob/main/mmdet/models/layers/dropblock.py

存在的问题

Dropout作为一种正则化方法，在卷积结构中很少使用，大多数情况下，dropout主要用于卷积网络的全连接层。作者认为dropout的主要缺点在于它是随机删除特征的，这对于全连接层有效，但对于特征空间相关spatially correlated的卷积层就不那么有效了。但特征相关联时，即使个别特征被删除了，输入的信息仍然传到下一层，从而导致网络过拟合。因此需要一种更结构化形式的dropout来对网络进行正则化。

本文的创新点

本文提出了DropBlock，一种结构化形式的dropout，特征图中一个连续相邻区域中的所有特征被一起丢弃，作者通过实验发现，除了在卷积层中，在skip connection中应用DropBlock也可以提高精度。此外在训练过程中，逐渐增加丢弃特征的数量可以进一步提高精度并且对超参的选择更加鲁棒。

方法介绍

DropBlock的伪代码如下所示

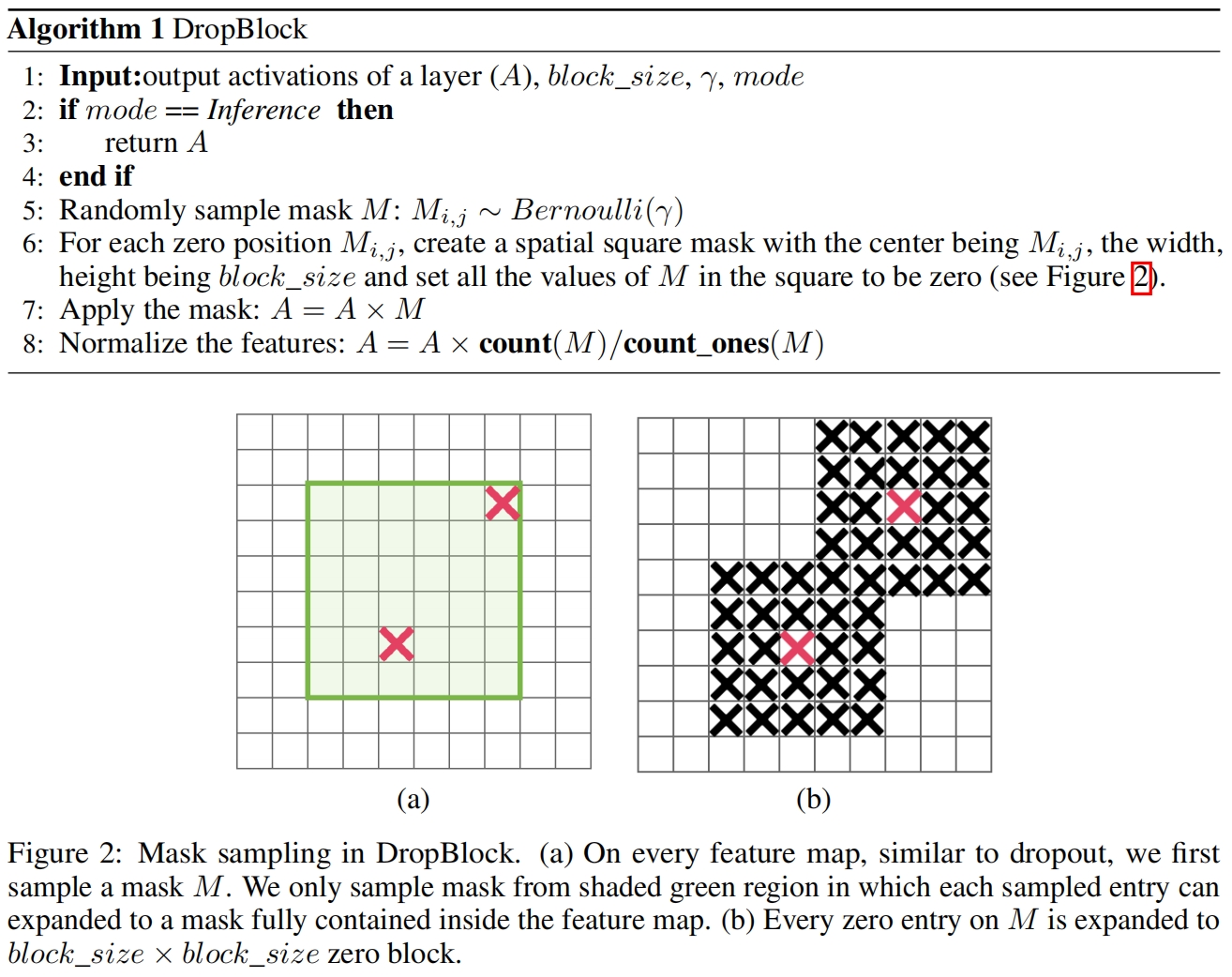
其中有两个参数 \(block\_size\) 和 \(\gamma\)，block_size是丢弃区域的大小，\(\gamma\) 控制丢弃特征的数量。

作者实验在不同的通道上共用一个DropBlock掩码和每个通道单独一个掩码，结果表明后者效果更好，算法1对应的是后者。

在具体实现中，所有的特征图的block_size设置为固定值，不管特征图的分辨率大小。

\(\gamma\) 通过下式计算得到

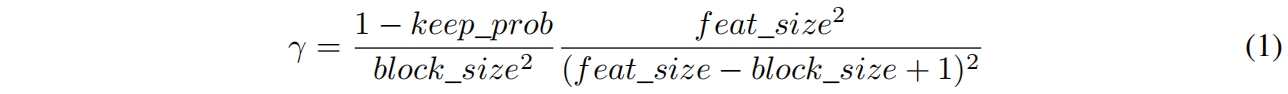
其中 \(keep\_prob\) 可以解释为dropout中保留一个特征unit的概率，\(feat\_size\) 是特征图的大小，有效种子区域的大小为 \((feat\_size-block\_size+1)^2\)，因为丢弃的区域可能会用重合，因此式(1)只是一个近似结果。

Scheduled DropBlock. 作者发现在训练过程中使用固定的 \(keep\_prob\) 的效果不佳，在训练刚开始时 \(keep\_prob\) 过小会影响模型的学习，因此作者采用了一个线性减小的方案，\(keep\_prob\) 从1逐渐减小到目标值，实验证明，这种方案在各种超参设置下的效果都很好。

代码解析

下面是mmdetection中的完整实现

# Copyright (c) OpenMMLab. All rights reserved.
import torch
import torch.nn as nn
import torch.nn.functional as F
from mmcv.cnn import PLUGIN_LAYERS

eps = 1e-6


@PLUGIN_LAYERS.register_module()
class DropBlock(nn.Module):
    """Randomly drop some regions of feature maps.

     Please refer to the method proposed in `DropBlock
     <https://arxiv.org/abs/1810.12890>`_ for details.

    Args:
        drop_prob (float): The probability of dropping each block.
        block_size (int): The size of dropped blocks.
        warmup_iters (int): The drop probability will linearly increase
            from `0` to `drop_prob` during the first `warmup_iters` iterations.
            Default: 2000.
    """

    def __init__(self, drop_prob, block_size, warmup_iters=2000, **kwargs):
        super(DropBlock, self).__init__()
        assert block_size % 2 == 1
        assert 0 < drop_prob <= 1
        assert warmup_iters >= 0
        self.drop_prob = drop_prob
        self.block_size = block_size
        self.warmup_iters = warmup_iters
        self.iter_cnt = 0

    def forward(self, x):
        """
        Args:
            x (Tensor): Input feature map on which some areas will be randomly
                dropped.

        Returns:
            Tensor: The tensor after DropBlock layer.
        """
        if not self.training:
            return x
        self.iter_cnt += 1
        N, C, H, W = list(x.shape)
        gamma = self._compute_gamma((H, W))
        mask_shape = (N, C, H - self.block_size + 1, W - self.block_size + 1)
        mask = torch.bernoulli(torch.full(mask_shape, gamma, device=x.device))

        mask = F.pad(mask, [self.block_size // 2] * 4, value=0)
        mask = F.max_pool2d(
            input=mask,
            stride=(1, 1),
            kernel_size=(self.block_size, self.block_size),
            padding=self.block_size // 2)
        mask = 1 - mask
        x = x * mask * mask.numel() / (eps + mask.sum())
        return x

    def _compute_gamma(self, feat_size):
        """Compute the value of gamma according to paper. gamma is the
        parameter of bernoulli distribution, which controls the number of
        features to drop.

        gamma = (drop_prob * fm_area) / (drop_area * keep_area)

        Args:
            feat_size (tuple[int, int]): The height and width of feature map.

        Returns:
            float: The value of gamma.
        """
        gamma = (self.drop_prob * feat_size[0] * feat_size[1])
        gamma /= ((feat_size[0] - self.block_size + 1) *
                  (feat_size[1] - self.block_size + 1))
        gamma /= (self.block_size**2)
        factor = (1.0 if self.iter_cnt > self.warmup_iters else self.iter_cnt /
                  self.warmup_iters)
        return gamma * factor

    def extra_repr(self):
        return (f'drop_prob={self.drop_prob}, block_size={self.block_size}, '
                f'warmup_iters={self.warmup_iters}')

我们可以直接用下面的代码进行测试，其中feat表示输入特征图，其中值的随机设定的，单通道大小为11x11。drop_prob=0.5和论文中keep_prob的关系是drop_prob=1-keep_prob。warmup_iters表示文中提到的线性减小keep_prob的迭代次数，即这里线性增大drop_prob的迭代次数。

feat = torch.rand(1, 1, 11, 11)
drop_prob = 0.5
dropblock = DropBlock(drop_prob, block_size=5, warmup_iters=0)
out_feat = dropblock(feat)

函数_compute_gamma对应式(1)，最后一行的factor相当于一个缩放因子，迭代从0到warmup_iters，factor的值从0线性增大到1，之后保持不变。这里计算得到的gamma值为0.0494。

然后mask_shape大小为原始输入大小减去block_size，这里为7x7。torch.bernoulli的输入是一个7x7的矩阵，其中所有值都是0.494，表示每个位置有0.0494的概率为1。输出mask是一个7x7大小的0,1矩阵，如下

tensor([[[[0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 1.],
          [0., 0., 0., 0., 0., 0., 0.],
          [1., 0., 0., 0., 0., 0., 0.]]]])

?然后四周补0，pad回11x11大小。如下

tensor([[[[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]]]])

然后通过max pooling的方式根据block_size进行外扩，即图2中(a)到(b)的过程，如下

tensor([[[[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 1.],
          [0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1.],
          [1., 1., 1., 1., 1., 0., 0., 0., 0., 0., 0.],
          [1., 1., 1., 1., 1., 0., 0., 0., 0., 0., 0.]]]])

最后1-mask这两个block处的值置为0，然后与原始输入相乘，并进行归一化，mask.numel()求得是mask中的元素个数，mask.sum()求的是mask中所有元素值的和，这里分别为121和71。

实验结果

从下表可以看出，在ResNet-50上，DropBlock的效果要优于dropout以及其它正则方法和数据增强。

对于ResNet-50，keep_prob=0.9，block_size=7，将dropblock应用到group3、4，并结合label smooth的效果是最好的。?