汉诺塔(Tower of Hanoi)问题（Ｃ语言）（学不会，你来找我）

1.汉诺塔问题简述

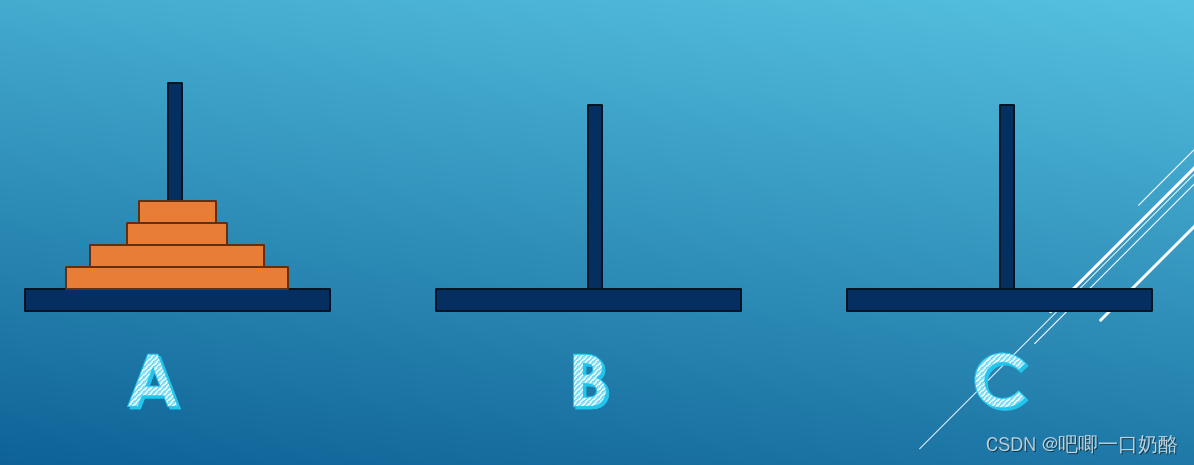
古代有一个梵塔，塔内有A,B,C3个座，座A上有64个大小不等的盘子，大的在下，小的在上，如下图所示。有一个和尚想把这64个盘子从座A全部移动到座C，在移动过程中可以借助座A,座B和座C，但每次只允许移动一个盒子，并且不允许大盘放在小盘的上面。要求打印移动的步骤。

2.编程思路

我们进行如下设想：

（1）先将上面的63个盘子看成一个整体，从座A移到座B。

（2）再将剩下的1个盘子（第64个）从座A移到座C。

（3）最后将这63个盘子看成一个整体，从座B移到座C。

这样通过上述3步将64个盘子的问题化简成63个盘子的问题，在用类似的3步，可以将63个盘子的问题化简成62个盘子的问题。以此类推，最终可以将问题化简成一个盘子的问题，而一个盘子可以直接移动，从而解决问题。（相信有许多小伙伴到这还是没懂，萌萌的）

为了解决小伙伴心中的疑惑，我用图片形式来解释（先以4个盘子为例）

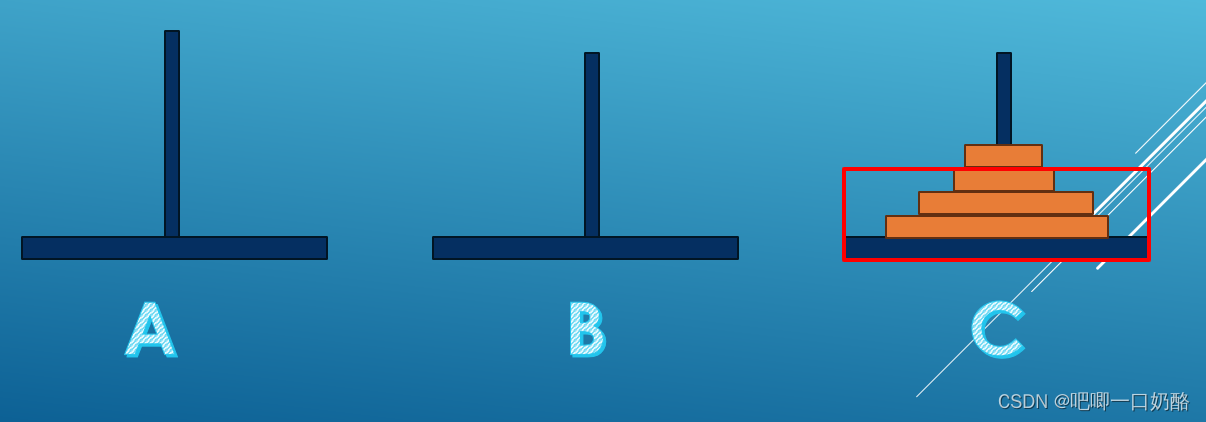
（1）先将上面的3个盘子看成一个整体，从座A移到座B，再将剩下的1个盘子（第4个）从座A移到座C。

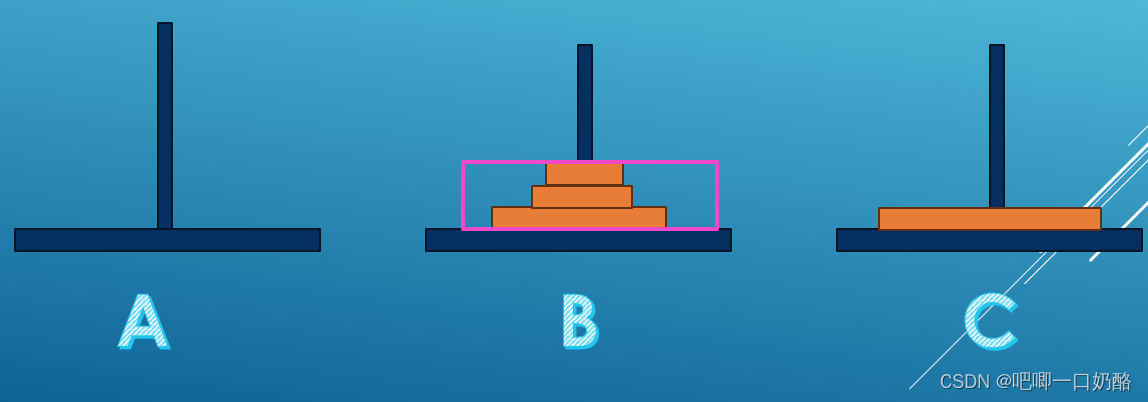
?（2）最后将这3个盘子看成一个整体，从座B移到座C（桃红框里的为一个整体）。

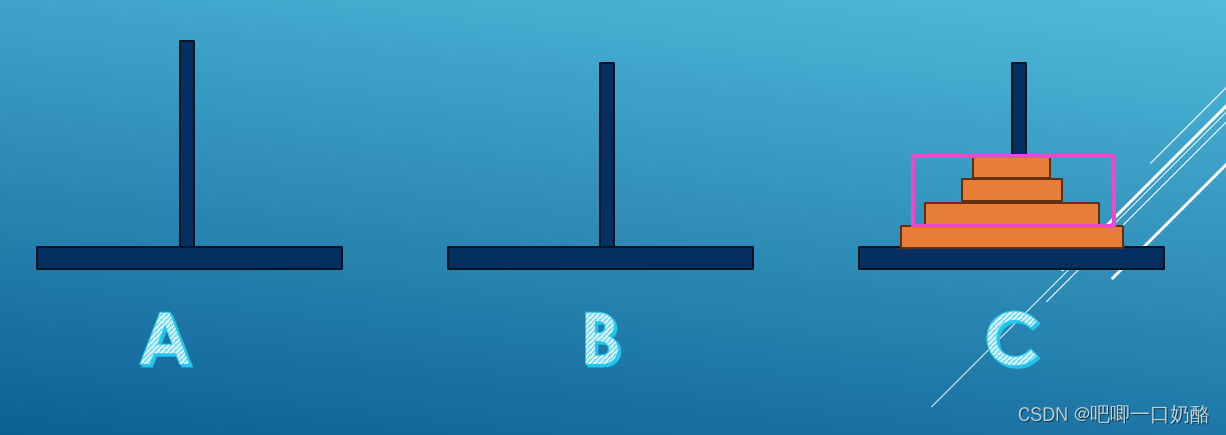
（3）这时我们将这个4个盘子问题化简成3个盘子问题，分析上图桃红框里的那三块，化简以后如下图所示（将红框里的看成底座）。

（4）先将上面的2个盘子看成一个整体，从座A移到座B，再将剩下的1个盘子（第3个）从座A移到座C。

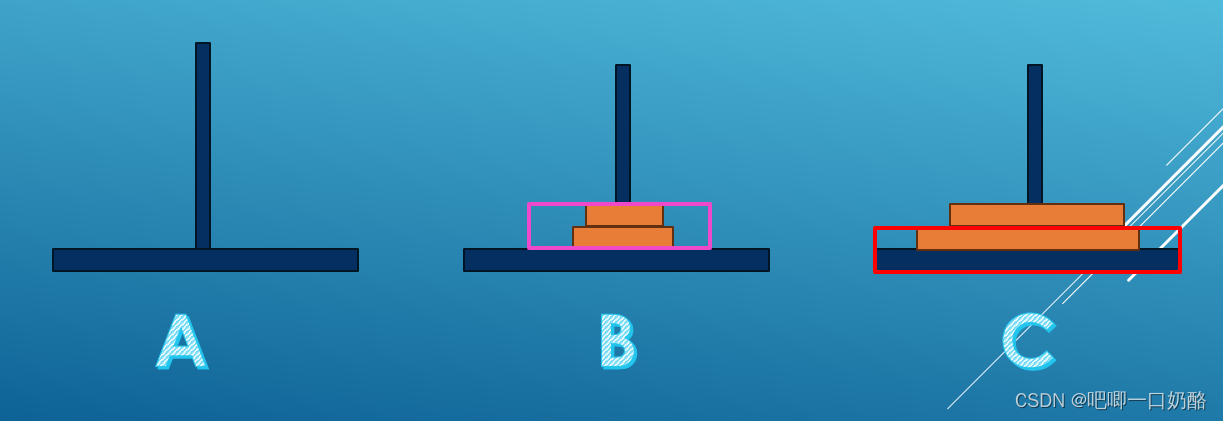
??（5）最后将这2个盘子看成一个整体，从座B移到座C（桃红框里的为一个整体，红框里的为底座）。

?（6）这时我们将这个3个盘子问题化简成2个盘子问题，分析上图桃红框里的那两块，化简以后如下图所示（红框为底座）

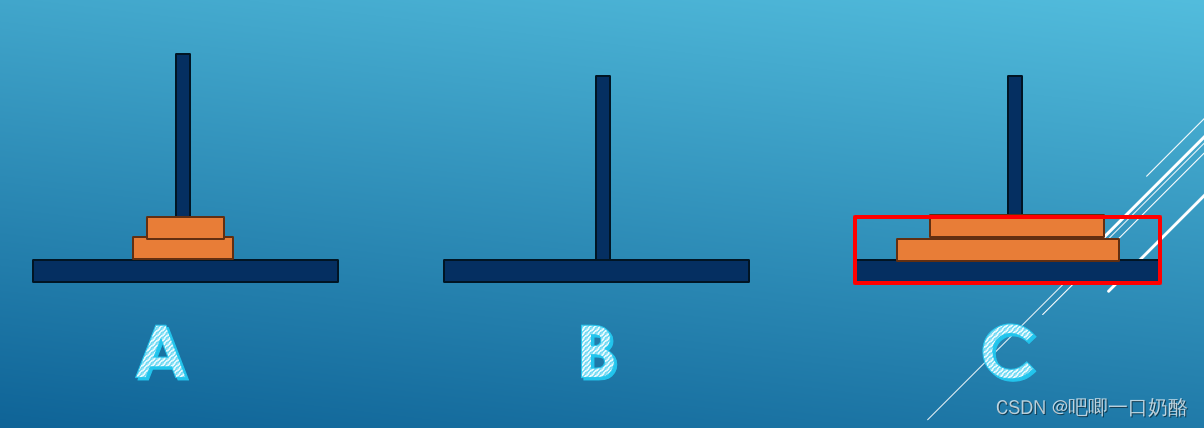
?（7）先将上面的1个盘子从座A移到座B，再将剩下的1个盘子（第2个）从座A移到座C。

（8）最后将这1个盘子从座B移到座C（红框为底座）。?

?

?（9）这时我们将这个2个盘子问题化简成1个盘子问题，化简以后如下图所示（红框为底座）

（9） 此时只需要将座A上的盘子移动到座C。

3.经过上述，我们可以描述为

?（1）将n-1个盘子从座A，借助座从，移到座B。

（2）将剩下的一个盘子从座A移到座C。

（3）将n-1个盘子从座B，借助座A，移到座C。

4.程序设计

#include <stdio.h>

//定义递归函数，将n个盘子从座A，借助座B，移到座C
void TowerofHanoi(int n, char A, char B, char C)
{
	if (n == 1)
		printf("从%c到%c\n", A, C);	//终止条件，只有1个盘子，可以直接移动
	else
	{
		TowerofHanoi(n - 1, A, C, B);
		printf("从%c到%c\n", A, C);
		TowerofHanoi(n - 1, B, A, C);
	}
}

int main()
{
	int m;
	while (1)
	{
		printf("请输入盘子的个数:");
		scanf("%d,%d", &m);
		printf("%d个盘子移动的步骤如下：\n");
		TowerofHanoi(m, 'A', 'B', 'C');
	}
	return 0;
}

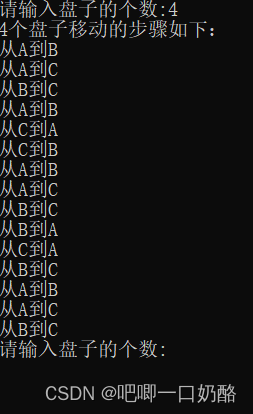
5.运行结果

由于64个得运行半天，就用了4个，有兴趣的小伙伴可以试一试64个