20文章解读与程序——@@@@EI\CSCD\北大核心《基于主从博弈的智能小区代理商定价策略及电动汽车充电管理》已提供下载资源

👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆下载资源链接👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆

这个标题涉及到两个主要方面：智能小区代理商的定价策略和电动汽车充电管理，而这两者都是基于主从博弈的理论框架来进行研究和设计的。

1. 主从博弈： 这是博弈论中的一种模型，涉及到参与者之间的相互作用和决策。在这种情境下，存在一个主体（主）和一个从属体（从），它们通过相互作用和协调来达成决策。这种博弈理论常被应用在经济学、管理学等领域，用于分析参与者之间的策略和互动。

2. 智能小区代理商定价策略： 这指的是在一个智能小区中，代理商（可能是自动化系统、算法或其他决策实体）采用主从博弈的理论框架来制定定价策略。代理商可能是主导者，而智能小区内的其他参与者可能是从属者。定价策略的制定可能涉及到资源分配、服务提供、能源管理等方面。

3. 电动汽车充电管理： 这表示研究范围还包括了电动汽车充电的问题。这可能涉及到在智能小区中管理电动汽车充电的时机、速率、能源成本等方面的决策。主从博弈的理论框架可能用于解决代理商与电动汽车用户之间的互动和决策过程。

因此，整个标题的含义是在一个智能小区的背景下，通过应用主从博弈的理论框架，研究智能小区代理商的定价策略以及与电动汽车充电管理相关的决策过程。这表明研究的焦点在于理解和优化代理商在智能小区环境下的定价决策，并且考虑到电动汽车充电管理的方面。

摘要：智能电网的负荷包括传统负荷和主动负荷，我国配电 网侧的主动负荷主要由电动汽车构成，功率需求随电价变化 是其重要特点之一。随着电动汽车的普及，代理商将在小区 电动汽车充电管理中扮演重要角色。如何制定代理商的定价 与购电策略，实现代理商与电动汽车车主双赢，成为重要的研究课题。基于以上原因，提出了一种未来智能小区代理商 的定价及购电策略，将代理商和车主各自追求利益最大化建 模为主从博弈。该模型亦可为研究电动汽车参与的需求侧响 应提供重要的借鉴。另外，还进一步通过 Karush-KuhnTucker 最优性条件和线性规划对偶定理将此博弈模型转化 为混合整数线性规划问题进行求解，最终获得全局最优的定 价策略。

这段摘要涉及到智能电网中的负荷管理，特别是涉及到电动汽车的主动负荷。以下是对摘要的详细解读：

1. 智能电网的负荷： 智能电网的负荷可以分为传统负荷和主动负荷。传统负荷可能指的是传统的电力需求，而主动负荷则主要由电动汽车构成。

2. 电动汽车构成的主动负荷： 在我国的配电网侧，电动汽车构成了主要的主动负荷。这意味着电动汽车对电网的功率需求具有显著的影响，并且这个需求会随电价的变化而变化。

3. 代理商在电动汽车充电管理中的角色： 随着电动汽车的普及，代理商在小区电动汽车充电管理中变得至关重要。代理商可能是负责管理电动汽车充电的实体，其任务包括制定定价和购电策略。

4. 定价与购电策略的制定： 摘要指出，如何制定代理商的定价与购电策略成为一个重要的研究课题。这涉及到平衡代理商与电动汽车车主之间的利益，实现双赢的目标。

5. 主从博弈建模： 为解决这一问题，摘要提出了一种未来智能小区代理商的定价及购电策略，将代理商和车主各自追求利益最大化建模为主从博弈。这意味着代理商和车主在定价与购电方面存在相互影响和冲突。

6. 线性规划求解： 为了得到最优的定价策略，摘要还提到通过 Karush-Kuhn-Tucker 最优性条件和线性规划对偶定理，将主从博弈模型转化为混合整数线性规划问题进行求解。这是一种数学方法，用于优化博弈模型，最终得到全局最优的定价策略。

总体而言，这段摘要关注智能电网中电动汽车充电管理的问题，通过主从博弈的模型，强调了代理商与电动汽车车主之间利益平衡的重要性，并提供了一种通过线性规划求解最优策略的方法。

部分代码展示：

%三层博弈，电网-充电站-用户
%电网-充电站，合作博弈，Pareto均衡
%充电站-用户，主从博弈，KKT条件
clear
clc
%%%%主从博弈%%%
PL=[1733.66666666000;1857.50000000000;2105.16666657000;2352.83333343000;2476.66666657000;2724.33333343000;2848.16666657000;2972;3219.66666657000;3467.33333343000;3591.16666657000;3715.00000000000;3467.33333343000;3219.66666657000;2972;2600.50000000000;2476.66666657000;2724.33333343000;2972;3467.33333343000;3219.66666657000;2724.33333343000;2229;1981.33333343000];
a=0.55*PL/mean(PL);
b=0.55/mean(PL)*ones(24,1);;
%b=zeros(24,1);
lb=0.2;
ub=1;
T_1=[1;1;1;1;1;1;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;1;1;1];%%%早出晚归型
T_2=[1;1;1;1;1;1;1;1;0;0;0;0;1;1;1;0;0;0;0;1;1;1;1;1];%%%上班族
T_3=[0;0;0;0;0;0;0;1;1;1;1;1;1;1;1;1;1;1;1;1;0;0;0;0];%%%夜班型
Ce=sdpvar(24,1);%电价
Pb=sdpvar(24,1);%购电
Pc1=sdpvar(24,1);%一类车充电功率
Pc2=sdpvar(24,1);%二类车充电功率
Pc3=sdpvar(24,1);%三类车充电功率
C=[lb<=Ce<=ub,mean(Ce)==0.7,Pb>=0];%边界约束
C=[C,Pc1+Pc2+Pc3==Pb];%能量平衡
L_u=sdpvar(1,3);%电量需求等式约束的拉格朗日函数
L_lb=sdpvar(24,3);%充电功率下限约束的拉格朗日函数
L_ub=sdpvar(24,3);%充电功率上限约束的拉格朗日函数
L_T=sdpvar(24,3);%充电可用时间约束的拉格朗日函数
f=200*L_u(1)*(0.9*42-9.6)+150*L_u(2)*(0.9*42-9.6)+50*L_u(3)*(0.9*42-9.6)+sum(sum(L_ub).*[32*30,32*30,16*30])-sum(a.*Pb+b.*Pb.^2);%目标函数
C=[C,Ce-L_u(1)*ones(24,1)-L_lb(:,1)-L_ub(:,1)-L_T(:,1)==0,Ce-L_u(2)*ones(24,1)-L_lb(:,2)-L_ub(:,2)-L_T(:,2)==0,Ce-L_u(3)*ones(24,1)-L_lb(:,3)-L_ub(:,3)-L_T(:,3)==0];%KKT条件
C=[C,sum(Pc1)==200*(0.9*42-9.6),sum(Pc2)==150*(0.9*42-9.6),sum(Pc3)==50*(0.9*42-9.6)];%电量需求约束
for t=1:24
    if T_1(t)==0
        C=[C,Pc1(t)==0];
    else
        C=[C,L_T(t,1)==0];
    end
    if T_2(t)==0
        C=[C,Pc2(t)==0];
    else
        C=[C,L_T(t,2)==0];
    end
    if T_3(t)==0
        C=[C,Pc3(t)==0];
    else
        C=[C,L_T(t,3)==0];
    end

效果展示：

20号资源-源程序：论文可在知网下载《基于主从博弈的智能小区代理商定价策略及电动汽车充电管理》本人博客有解读资源-CSDN文库https://download.csdn.net/download/LIANG674027206/88728051

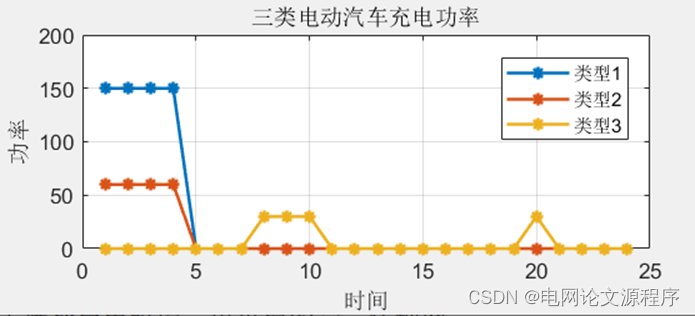
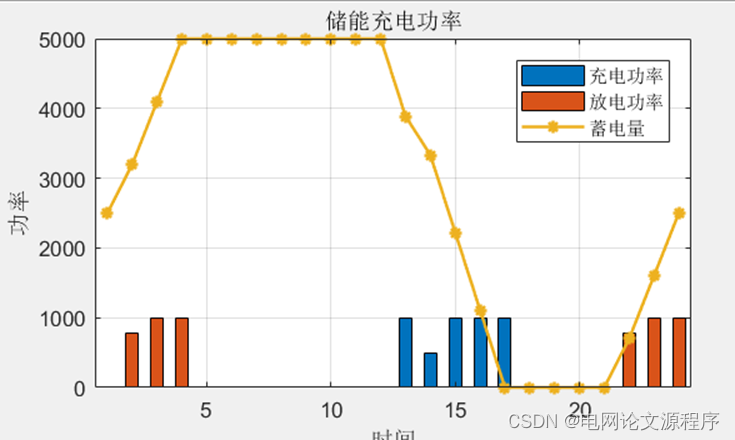
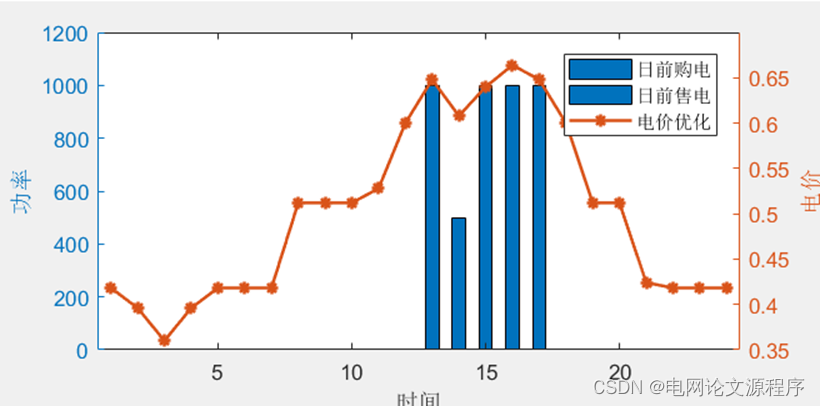
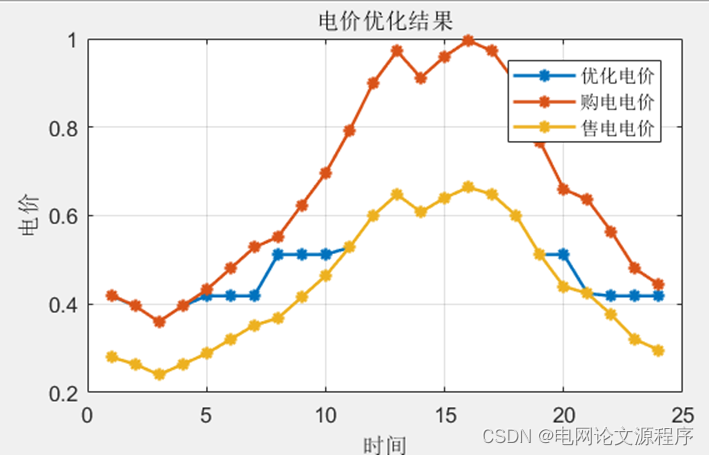
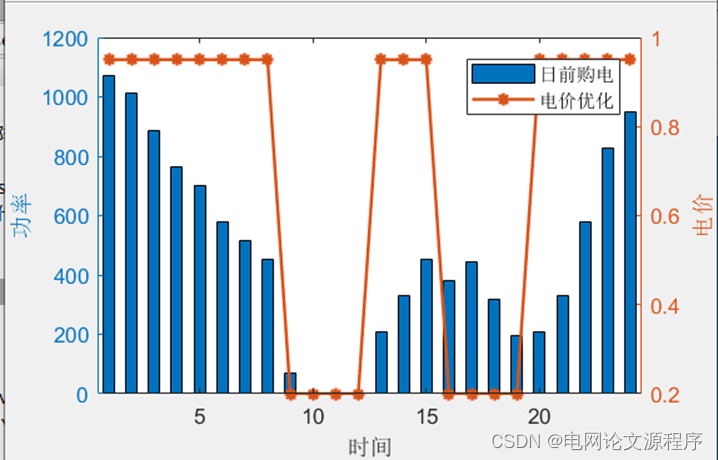
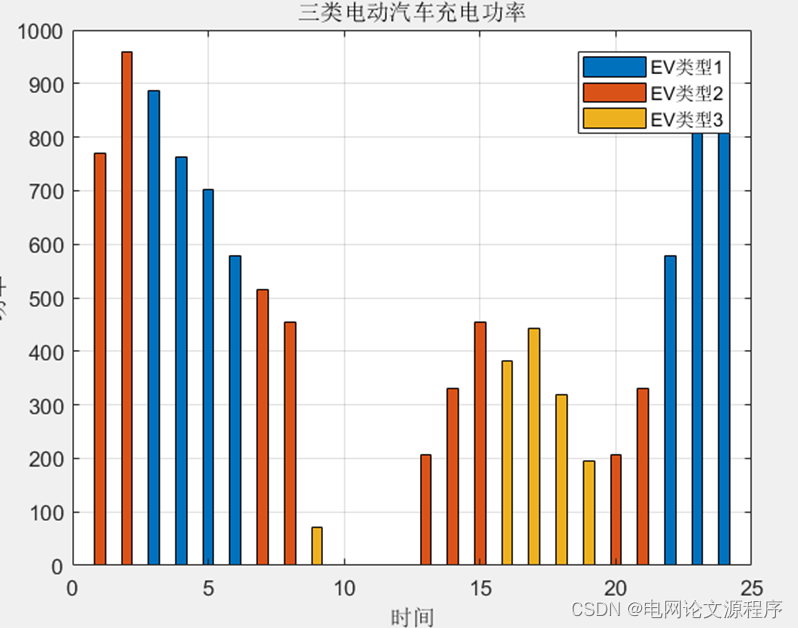
👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆下载资源链接👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆