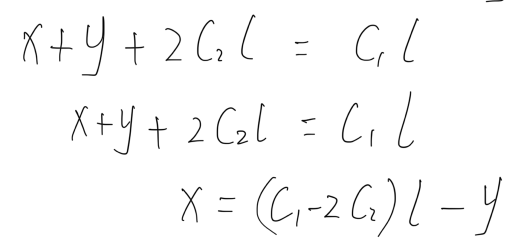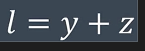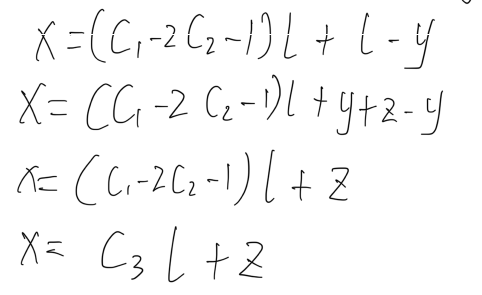弗洛伊德循环查找算法-原理

本文灵感来自哔哩哔哩视频?

视频链接:

弗洛伊德循环查找算法

算法代码(java)

package rain;

class ListNode {
    int value;
    ListNode next;

    public ListNode(int value) {
        this.value = value;
        this.next = null;
    }

    @Override
    public String toString() {
        return "ListNode{" +
                "value=" + value +
                '}';
    }
}
public class FloydCycleDetectionAlgrithm {
    public static void main(String[] args) {
        ListNode node0 = new ListNode(4);
        ListNode node1 = new ListNode(3);
        ListNode node2 = new ListNode(7);
        ListNode node3 = new ListNode(8);
        ListNode node4 = new ListNode(6);
        ListNode node5 = new ListNode(9);
        ListNode node6 = new ListNode(2);
        ListNode node7 = new ListNode(1);
        ListNode node8 = new ListNode(5);
        ListNode node9 = new ListNode(2);

        node0.next = node4;
        node1.next = node3;
        node2.next = node7;
        node3.next = node8;
        node4.next = node6;
        node5.next = node9;
        node6.next = node2;
        node7.next = node1;
        node8.next = node5;
        node9.next = node2;

        ListNode node = Find(node0);
        System.out.println(node);
    }
    public static ListNode Find(ListNode head) {
        ListNode slow  = head;
        ListNode fast = head;

        while (true) {
            slow = slow.next;
            fast = fast.next.next;
            //第一次相遇
            //if slow and fast meet, then break the loop
            if (fast == slow) {
                break;
            }
        }
        //第二次相遇
        slow = head;
        while (true) {
            slow = slow.next;
            fast = fast.next;
            if (fast == slow) {
                return fast;
            }
        }
    }
}

弗洛伊德循环查找算法中第二次相遇的地方就是循环的起始点，这个性质的证明是基于数学的原理。这是因为在第一次相遇时，慢指针 `slow` 和快指针 `fast` 已经处于同一个循环内。设链表起点到环的起始点的距离为 X，环的起始点到第一次相遇点的距离为 Y，第一次相遇点到环的起始点的距离为Z。

第一次相遇

 ListNode slow  = head;
        ListNode fast = head;

        while (true) {
            slow = slow.next;
            fast = fast.next.next;
            //第一次相遇
            //if slow and fast meet, then break the loop
            if (fast == slow) {
                break;
            }
        }

设循环长度

1. 在第一次相遇时，慢指针 `slow` 走的距离，

C2是常数

而快指针 `fast` 走?的距离

2. 由于快指针的速度是慢指针的两倍，所以快指针走的距离是慢指针的两倍。因此，有

3. 进一步简化上述等式，得到

这意味着

循环前的距离X = 一定数量循环次数 减去 汇合点前距离Y

4.因为

可得

C3乘以 循环长度长度l 意味着固定的循环量！

找到节点只需要让两个节点分别走X和C3l+Z的路程

此时, 我们可以把slow放在起始位置 每次走一格,?

同时 让fast也是每次走一格

直到相遇 fast == slow 说明相遇的节点就是循环开始的节点

//第二次相遇
        slow = head;
        while (true) {
            slow = slow.next;
            fast = fast.next;
            if (fast == slow) {
                return fast;
            }
        }

也就是说，如果此时将慢指针重新指向链表起始点，慢指针再次移动 X 的距离，而快指针从第一次相遇点开始移动 C3l+Z 的距离，它们将会在环的起始点再次相遇。

因此，第二次相遇的地方就是循环的起始点。这个性质是弗洛伊德循环查找算法的关键之一，也是该算法能够正确找到环的起始点的原因。

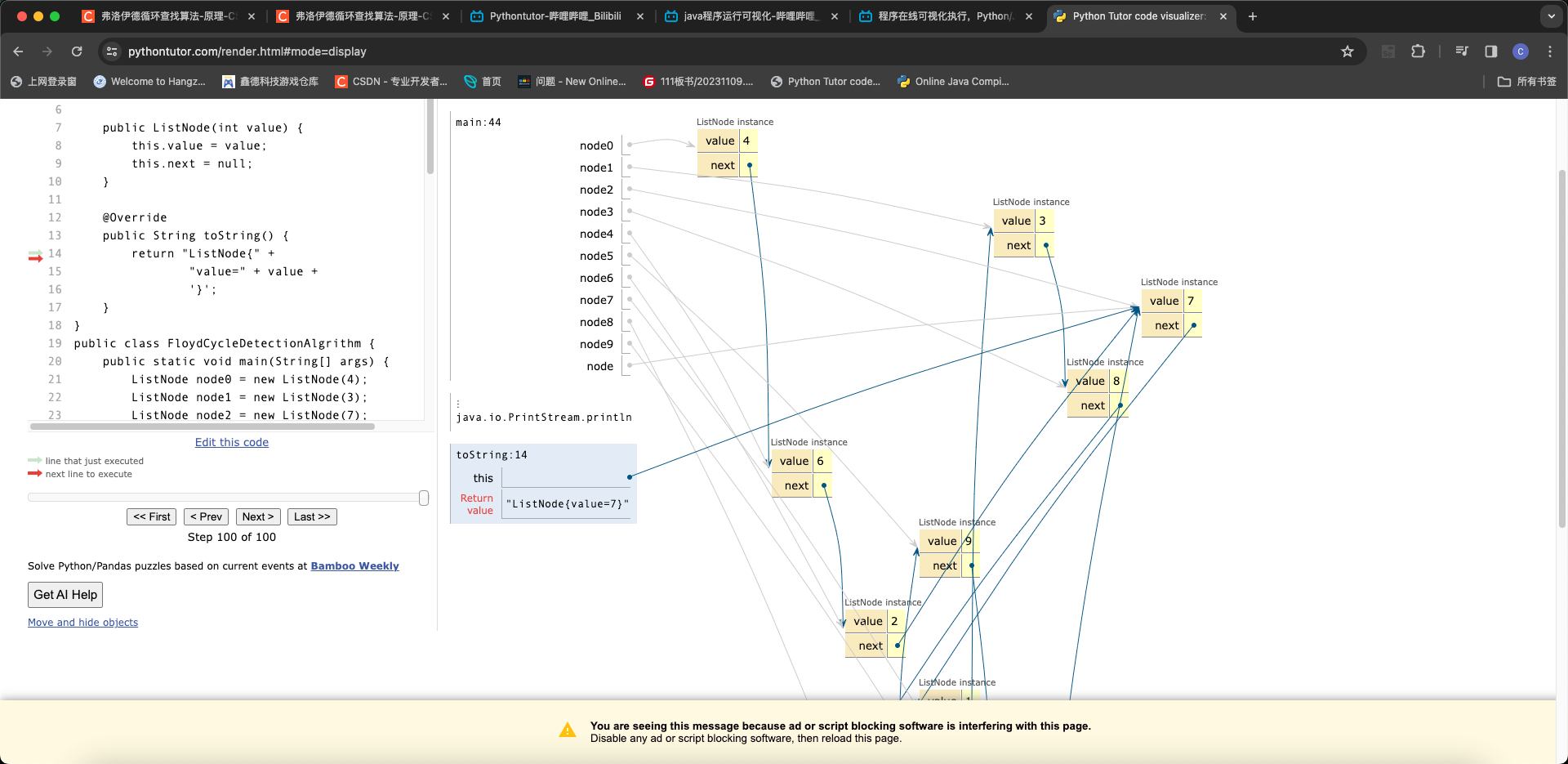
文末推荐我常用的一个学习网站 可视化运行程序

比如这段链表就可以直观展示出来

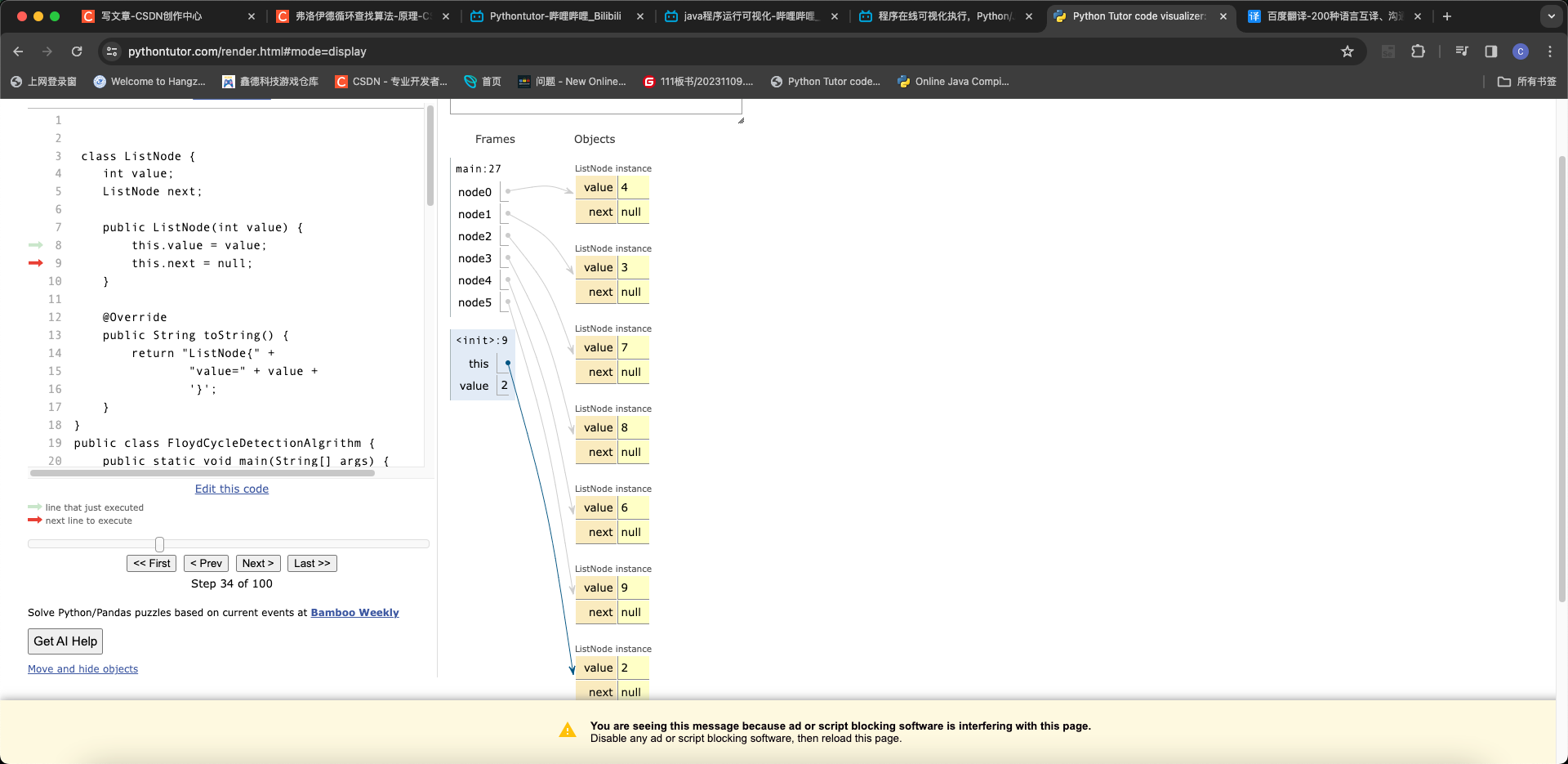
网站链接

可视化运行网站

?