【代码随想录】刷题笔记Day53

前言

• 不用开组会的我是多么阳光开朗，这周就要离开杭州回家啦，多刷题刷题

115. 不同的子序列 - 力扣（LeetCode）

• dp[i][j]
  • 以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]
• 递推公式
  • dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
  • 
• ?初始化
  • dp[i][0] = 1，dp[0][j] = 0，dp[0][0] = 1，遍历从上到下，从左到右
• 

• class Solution {
  public:
      int numDistinct(string s, string t) {
          vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1));
          for (int i = 0; i < s.size(); i++) dp[i][0] = 1;
          for (int j = 1; j < t.size(); j++) dp[0][j] = 0;
          for (int i = 1; i <= s.size(); i++) {
              for (int j = 1; j <= t.size(); j++) {
                  if (s[i - 1] == t[j - 1]) {
                      dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                  } else {
                      dp[i][j] = dp[i - 1][j];
                  }
              }
          }
          return dp[s.size()][t.size()];
      }
  };

?583. 两个字符串的删除操作 - 力扣（LeetCode）

• 思路一

  • 求最长公共子序列，再求每个串相减所需要的步数，相加

  • class Solution {
    public:
        int minDistance(string word1, string word2) {
            // 求最长公共子序列（不连续）
            int len1 = word1.size();
            int len2 = word2.size();
            int maxlen = 0;
            vector<vector<int>> dp (len1 + 1, vector<int>(len2 + 1, 0));
            for (int i = 1; i <= len1; i++) {
                for (int j = 1; j <= len2; j++) {
                    if(word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                    else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                    maxlen = max(dp[i][j], maxlen);
                }
            }
            // 求每个串减去公共子序列需要的步数，相加
            return len1 + len2 - 2 * maxlen;
        }
    };

• 思路二

  • ?编辑子串思路，两个字符串都可以进行删除操作
  • dp[i][j]含义
    • 以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，达到相等所需要删除元素的最少次数
  • 递推公式
    • 当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1][j - 1];
    • 当word1[i - 1] 与 word2[j - 1]不相同的时候
      • 情况一：删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1
      • 情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1
      • 情况三：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2
      • dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
      • 可简化为dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
  • 初始化
    • 空字符串要全删，dp[i][0] = i，dp[0][j] = j，从上到下从左到右
  • 

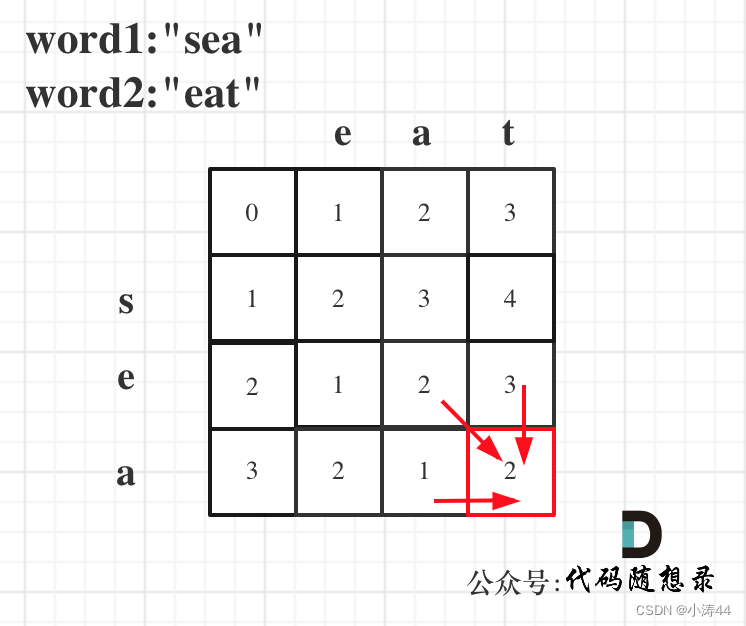
  • class Solution {
    public:
        int minDistance(string word1, string word2) {
            int len1 = word1.size();
            int len2 = word2.size();
            vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1));
            for(int i = 0; i <= len1; i++) dp[i][0] = i;
            for(int j = 0; j <= len2; j++) dp[0][j] = j;
            for(int i = 1; i <= len1; i++){
                for(int j = 1; j <= len2; j++){
                    if(word1[i-1] == word2[j-1]){
                        dp[i][j] = dp[i-1][j-1];
                    }else{
                        dp[i][j] = min(dp[i-1][j] + 1, dp[i][j-1] + 1);
                    }
                }
            }
            return dp[len1][len2];
        }
    };

?72. 编辑距离 - 力扣（LeetCode）

• 终极经典题目，暴力都没思路，1→2增删改，实际上是1→3←2删改
• dp[i][j]含义
  • 以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离（最小编辑次数）为dp[i][j]
• 递推公式

  • if(word1[i-1] == word2[j-1]){
        // 不操作
        dp[i][j] = dp[i-1][j-1];
    }else{
        // 增/删：dp[i-1][j] + 1, dp[i][j-1] + 1
        // 改：dp[i-1][j-1] + 1
        dp[i][j] = min(min(dp[i-1][j] + 1, dp[i][j-1] + 1), dp[i-1][j-1] + 1);
    }

• 初始化
  • ?空字符串要全删，dp[i][0] = i，dp[0][j] = j，从上到下从左到右
• 

• class Solution {
  public:
      int minDistance(string word1, string word2) {
          int len1 = word1.size();
          int len2 = word2.size();
          vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1));
          for(int i = 0; i <= len1; i++) dp[i][0] = i;
          for(int j = 0; j <= len2; j++) dp[0][j] = j;
          for(int i = 1; i <= len1; i++){
              for(int j = 1; j <= len2; j++){
                  if(word1[i-1] == word2[j-1]){
                      dp[i][j] = dp[i-1][j-1];
                  }else{
                      dp[i][j] = min(min(dp[i-1][j] + 1, dp[i][j-1] + 1), dp[i-1][j-1] + 1);
                  }
              }
          }
          return dp[len1][len2];
      }
  };

后言

• 下篇就是动规dp最后一篇啦，今天一次性搞完，心情鸡冻~?