强化学习的数学原理学习笔记 - Actor-Critic

---

本系列文章介绍强化学习基础知识与经典算法原理，大部分内容来自西湖大学赵世钰老师的强化学习的数学原理课程（参考资料1），并参考了部分参考资料2、3的内容进行补充。

系列博文索引：

• 强化学习的数学原理学习笔记 - RL基础知识
• 强化学习的数学原理学习笔记 - 基于模型（Model-based）
• 强化学习的数学原理学习笔记 - 蒙特卡洛方法（Monte Carlo）
• 强化学习的数学原理学习笔记 - 时序差分学习（Temporal Difference）
• 强化学习的数学原理学习笔记 - 值函数近似（Value Function Approximation）
• 强化学习的数学原理学习笔记 - 策略梯度（Policy Gradient）
• 强化学习的数学原理学习笔记 - Actor-Critic

参考资料：

1. 【强化学习的数学原理】课程：从零开始到透彻理解（完结）（主要）
2. Sutton & Barto Book: Reinforcement Learning: An Introduction
3. 机器学习笔记

*注：【】内文字为个人想法，不一定准确

概览：RL方法分类

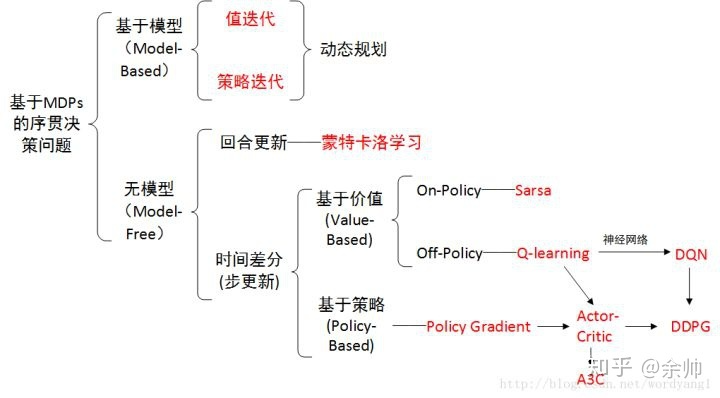
*图源：https://zhuanlan.zhihu.com/p/36494307

Actor-Critic

Actor-Critic属于策略梯度（PG）方法，实际上是将值函数近似和策略梯度方法进行了结合。

• Actor：策略更新，Actor用来执行动作与环境交互
• Critic：策略评估 / 值估计，Critic用来评估Actor的好坏

Basic actor-critic / QAC

与策略梯度算法对应，Actor即为策略梯度算法中执行策略更新的部分（通过更新参数$\theta$），而Critic是估计$q_t(s_t,a_t)$的算法。QAC（Q actor-critic）是最简单的actor-critic算法，也是一种on-policy方法。

QAC vs. REINFOCE：估计$q_t(s_t,a_t)$的方法不同

• REINFORCE：蒙特卡洛（MC）
• QAC：时序差分（TD）

QAC算法：【简单理解：QAC = Sarsa with function estimation + Policy Gradient】

• Critic（值更新 / 策略评估）：采用Sarsa with function estimation的方法估计$q_t(s_t,a_t)$
  • $w_{t+1}=w_t+{\alpha }_w[r_{t+1}+\gamma q(s_{t+1},a_{t+1},w_t)?q(s_t,a_t,w_t)]{?}_{w}q(s_t,a_t,w_t)$
• Actor（策略更新 / 策略提升）：采用策略梯度（PG）的方法（同REINFROCE）更新策略
  • ${\theta }_{t+1}={\theta }_t+{\alpha }_{\theta }{?}_{\theta }\ln \pi (a_t|s_t,{\theta }_t)q_t(s_t,a_t,w_{t+1})$

🟦A2C (Advantage actor-critic)

A2C的基本思想：在QAC中引入baseline来减少估计的方差（variance）。

理论基础：引入baseline $b(S)$后，策略梯度（期望）不会发生改变，但其方差会减小（推导略），即 ${?}_{\theta }J(\theta )={\mathbb{E}}_{S～\eta ,A～\pi }[{?}_{\theta }\ln \pi (A|S,\theta )q_{\pi }(S,A)]={\mathbb{E}}_{S～\eta ,A～\pi }[{?}_{\theta }\ln \pi (A|S,\theta )(q_{\pi }(S,A)?b(S))]$ 其中，$b(S)$为关于$S$的标量函数。
使得方差最小的最优baseline形式为：$b^{?}(s)=\frac{{\mathbb{E}}_{A～\pi }[\Vert {?}_{\theta }\ln \pi (A|s,{\theta }_t){\Vert }^{2}q(S,A)]}{{\mathbb{E}}_{A～\pi }[\Vert {?}_{\theta }\ln \pi (A|s,{\theta }_t){\Vert }^2]}$
但直接应用此式过于复杂，因此在实际中选择次优baseline，去掉权重项$\Vert {?}_{\theta }\ln \pi (A|s,{\theta }_t){\Vert }^2$，有： $b(s)={\mathbb{E}}_{A～\pi }[q(S,A)]=v_{\pi }(s)$
即将$s$的状态值作为baseline。

在actor（策略更新）中引入状态值作为baseline，即：
$$\begin{array}{rl}{\theta }_{t+1}& ={\theta }_t+\alpha \mathbb{E}[{?}_{\theta }\ln \pi (A|S,{\theta }_t)[q_{\pi }(S,A)?v_{\pi }(S)]]\\ & ={\theta }_t+\alpha \mathbb{E}[{?}_{\theta }\ln \pi (A|S,{\theta }_t){\delta }_{\pi }(S,A)]\end{array}$$
其中，${\delta }_{\pi }(S,A)=q_{\pi }(S,A)?v_{\pi }(S)$是优势函数（advantage function），表示当前状态下的特定动作相对于当前策略的优势。对应的随机采样公式为：
$$\begin{array}{rl}{\theta }_{t+1}& ={\theta }_t+\alpha {?}_{\theta }\ln \pi (a_t|s_t,{\theta }_t)[q_t(s_t,a_t)?v_t(s_t)]\\ & ={\theta }_t+\alpha {?}_{\theta }\ln \pi (a_t|s_t,{\theta }_t){\delta }_t(s_t,a_t)\end{array}$$
进一步地，优势函数可以由TD error近似（推导略），好处是只需要一个神经网络近似$v_t$即可，不需要再近似$q_t$。这就是A2C（也称为TD actor-critic）算法，其优势函数的具体形式为：
$${\delta }_t=r_{t+1}+\gamma v_t(s_{t+1})?v_t(s_t)$$
*注：

• 优势函数在文献中通常记作$A$
• 这里的直觉是，动作值的相对值比其绝对值更重要

A2C的完整算法（on-policy）：

• TD error（优势函数）：${\delta }_t=r_{t+1}+\gamma v_t(s_{t+1})?v_t(s_t)$
• Critic（值更新 / 策略评估）：$w_{t+1}=w_t+{\alpha }_w{\delta }_t{?}_{w}v(s_t,w_t)$
  • *注意这里与QAC的区别：QAC用的是Sarsa，A2C用的是TD，因此这里用状态值而非动作值
• Actor（策略更新 / 策略提升）：${\theta }_{t+1}={\theta }_t+{\alpha }_{\theta }{\delta }_t{?}_{\theta }\ln \pi (a_t|s_t,{\theta }_t)$

Off-policy AC

AC算法本身是on-policy的，但是可以通过重要性采样（Importance Sampling） 将其转为off-policy算法。
*实际上，重要性采样可以应用于任何需要求期望的算法（如MC、TD等）。

🟡重要性采样（Importance Sampling）

重要性采样：基于概率分布$p_1$上对随机变量$X$的采样，估计概率分布$p_0$上$X$的期望$\mathbb{E}[X]$。
*应用场景：难以直接在$p_0$上计算$X$的期望，但可以很容易在$p_1$上对进行$X$采样。例如：$p_0$是连续分布，或$p_0$的形式未知（如其为神经网络）。

$${\mathbb{E}}_{X～p_0}[X]=\sum _x{p}_0(x)x=\sum _x{p}_1(x)\underset{f(x)}{\underbrace{\frac{p_0(x)}{p_1(x)}x}}={\mathbb{E}}_{X～p_1}[f(X)]$$
其中，${\mathbb{E}}_{X～p_1}[f(X)]$可以由对$f(X)$的采样均值直接估计（大数定律），即：
$${\mathbb{E}}_{X～p_0}[X]\approx \bar{f}=\frac{1}{n}\sum _{i=1}^{n}f(x_i)=\frac{1}{n}\sum _{i=1}^n\frac{p_0(x_i)}{p_1(x_i)}{x}_i$$
其中，$\frac{p_0(x_i)}{p_1(x_i)}$是重要性权重（importance weight），其大于1表明$x_i$在$p_0$下被采样的概率更高，小于1表明在$p_1$下被采样的概率更高。

Off-policy PG

由行为策略$\beta$生成经验采样，目标是最大化下式：
$J(\theta )={\sum }_{s\in \mathcal{S}}{d}_{\beta }(s)v_{\pi }(s)={\mathbb{E}}_{S～d_{\beta }}[v_{\pi }(S)]$
其中，$d_{\beta }$为策略$\beta$下的平稳分布。（*注意此式与策略梯度中$J(\theta )$为平均状态值${\bar{v}}_{\pi }$时公式的区别）
对应的梯度为：
${?}_{\theta }J(\theta )={\mathbb{E}}_{S～\rho ,A～\beta }[\frac{\pi (A|S,\theta )}{\beta (A|S)}{?}_{\theta }\ln \pi (A|S,\theta )q_{\pi }(S,A)]$
式中$\rho$是一个状态分布，$\frac{\pi (A|S,\theta )}{\beta (A|S)}$是重要性权重。注意$A～\beta$而非$A～\pi$。

Off-policy AC

基于前文分析，Off-policy AC的算法为：
$\begin{array}{rl}{\theta }_{t+1}& ={\theta }_t+{\alpha }_{\theta }\frac{\pi (a_t|s_t,{\theta }_t)}{\beta (a_t|s_t)}{?}_{\theta }\ln \pi (a_t|s_t,{\theta }_t)[r_{t+1}+\gamma v_t(s_{t+1})?v_t(s_t)]\\ & ={\theta }_t+{\alpha }_{\theta }\frac{\pi (a_t|s_t,{\theta }_t)}{\beta (a_t|s_t)}{?}_{\theta }\ln \pi (a_t|s_t,{\theta }_t){\delta }_t(s_t,a_t)\end{array}$

算法步骤及伪代码类似于A2C，主要是多了重要性权重$\frac{\pi (a_t|s_t,{\theta }_t)}{\beta (a_t|s_t)}$。

🟦DPG (Deterministic AC)

先前的PG及AC算法均为随机性（stochastic）策略，实际上也存在确定性（deterministic）策略的AC算法，即DPG（Deterministic Policy Gradient）。
确定性策略相对于随机性策略的优势：随机性策略只能处理有限个动作的情况（比如，神经网络的输出是有限的），而确定性策略可以处理连续的动作空间。

确定性策略记作：$a=\mu (s,\theta )$，也可以简记为$\mu (s)$。
$\mu$是从状态空间$\mathcal{S}$到动作空间$\mathcal{A}$的映射，可以由神经网络表示。

DPG为off-policy方法（动作不依赖于具体策略），其梯度计算如下：
$$\begin{array}{rl}{?}_{\theta }J(\theta )& =\sum _{s\in \mathcal{S}}{\rho }_{\mu }(s){?}_{\theta }\mu (s)({?}_a{q}_{\mu }(s,a)){|}_{a=\mu (s)}\\ & ={\mathbb{E}}_{S～{\rho }_{\mu }}[{?}_{\theta }\mu (s)({?}_a{q}_{\mu }(s,a)){|}_{a=\mu (s)}]\end{array}$$
其中，${\rho }_{\mu }$是一个状态分布。$({?}_a{q}_{\mu }(s,a)){|}_{a=\mu (s)}$表示先对$q_{\mu }(s,a)$求关于$a$的梯度，再将其中$a$的替换为$\mu (s)$。
对应的随机梯度上升算法为：
$${\theta }_{t+1}={\theta }_t+{\alpha }_{\theta }{?}_{\theta }\mu (s_t)({?}_a{q}_{\mu }(s_t,a)){|}_{a=\mu (s)}$$

DPG算法步骤（伪代码）：
初始化：行为策略$\beta (a|s)$；确定性目标策略$\mu (s,{\theta }_0)$，其中${\theta }_0$为初始参数向量；值函数$v(s,w_0)$，其中$w_0$为初始参数向量。(*$\beta$也可以被替换为$\mu$+噪音)

目标：最大化$J(\theta )$
步骤：在每个episode的第$t$个时间步中，遵循行为策略$\beta$产生动作$a_t$并获得$r_{t+1}$和$s_{t+1}$

• TD error（优势函数）：${\delta }_t=r_{t+1}+\gamma q(s_{t+1},\mu (s_{t+1},{\theta }_t),w_t)?q(s_t,a_t,w_t)$
• Critic（值更新 / 策略评估）：$w_{t+1}=w_t+{\alpha }_w{\delta }_t{?}_{w}q(s_t,a_t,w_t)$，即TD+值函数估计
• Actor（策略更新 / 策略提升）：${\theta }_{t+1}={\theta }_t+{\alpha }_{\theta }{?}_{\theta }\mu (s_t,{\theta }_t)({?}_{a}q(s_t,a,w_{t+1})){|}_{a=\mu (s_t)}$

注意到DPG中包含了$q(s,a,w)$，其可以由两种方式确定：

• 线性函数：$q(s,a,w)={?}^T(s,a)w$，其中$?(s,a)$是特征向量。这是DPG原论文中采用的方法，缺陷在于特征向量的选择比较困难，且线性函数的拟合能力有限
• 神经网络：即后续的DDPG（Deep deterministic policy gradient）方法