1月18日代码随想录二叉树搜索、验证二叉搜索树

700.二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点?root?和一个整数值?val。

你需要在 BST 中找到节点值等于?val?的节点。 返回以该节点为根的子树。 如果节点不存在，则返回?null?。

示例 1:

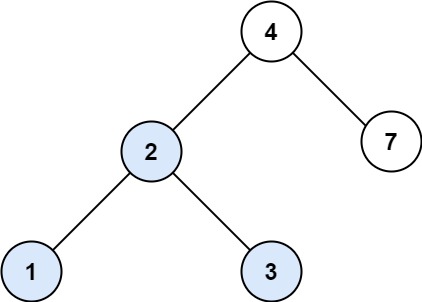
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

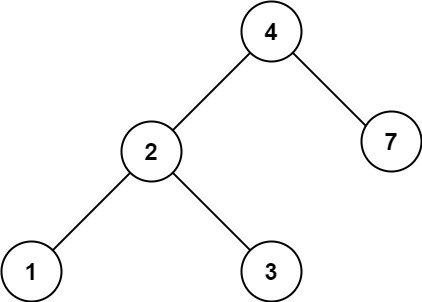
输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

• 树中节点数在?[1, 5000]?范围内
• 1 <= Node.val <= 107
• root?是二叉搜索树
• 1 <= val <= 107

思路

迭代法秒了，递归都不想看

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        while(root!=null){
            if (root.val == val) {
                return root;
            } else if (root.val > val) {
                root=root.left;
            }else {
                root=root.right;
            }
        }
        return null;
    }
}

98.验证二叉搜索树

给你一个二叉树的根节点?root?，判断其是否是一个有效的二叉搜索树。

有效?二叉搜索树定义如下：

• 节点的左子树只包含?小于?当前节点的数。
• 节点的右子树只包含?大于?当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

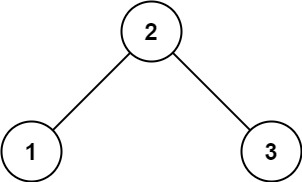
输入：root = [2,1,3]
输出：true

示例 2：

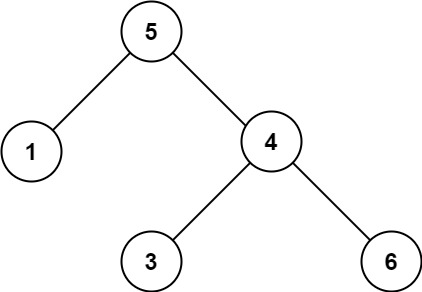
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104]?内
• -231 <= Node.val <= 231 - 1

思路

刚开始的想法是定义两个递归函数互相调用，一个判断左子树一个判断右子树，每次递归时把上一个节点的值记录下来传给下一个。

class Solution {
    public boolean isValidBST(TreeNode root) {
                if (root == null) {
            return false;
        }
        return isValidLeft(root.left,root.val)&&isValidRight(root.right,root.val);
    }
    public boolean isValidLeft(TreeNode node,int val){
        if (node == null) {
            return true;
        }
        if (node.val >= val) {
            return false;
        }
        return isValidLeft(node.left,node.val)&&isValidRight(node.right,node.val);
    }
    public boolean isValidRight(TreeNode node,int val){
        if (node == null) {
            return true;
        }
        if (node.val <= val) {
            return false;
        }
        return isValidLeft(node.left,node.val)&&isValidRight(node.right,node.val);
    }
} 

但这就犯了一个很严重的错误，就是只考虑每个节点的父节点的范围，没有考虑当前节点所在的整个子树，所以我们应该设置一个全局的值来判断是否为二叉搜索树。

class Solution {
    public boolean isValidBST(TreeNode root) {
        if(root==null){
            return false;
        }
        return isValid(root,Long.MIN_VALUE,Long.MAX_VALUE);
    }
    public boolean isValid(TreeNode node,long min,long max){
        if(node==null){
            return true;
        }
        if (node.val <= min || node.val >= max) {
            return false;
        }
        return isValid(node.left,min,node.val)&&isValid(node.right,node.val,max);
    }
    
}

迭代法：二叉搜索树的中序遍历一定是有序的，所以对二叉树进行中序遍历即可。

class Solution {
    public boolean isValidBST(TreeNode root) {
        Deque<TreeNode> stack=new LinkedList<TreeNode>();
        double inorder=-Double.MAX_VALUE;
        while(!stack.isEmpty()||root!=null){
            while (root != null) {
                stack.push(root);
                root=root.left;
            }
            root=stack.pop();
            if (root.val <= inorder) {
                return false;
            }
            inorder=root.val;
            root=root.right;
        }
        return true;
        
    }
}

总结

递归法一定要注意全局的条件，不能只继承上一次递归的。