yolo增加Shape-IoU，完美超越SIoU/EIoU/CIoU

论文地址：https://arxiv.org/pdf/2312.17663.pdf

代码地址：GitHub - malagoutou/Shape-IoU

摘要 作为检测定位分支的重要组成部分，边界框回归损失在目标检测任务中起着重要作用。现有的边界框回归方法通常考虑GT框和预测框之间的几何关系，通过相对位置和框形来计算损失，而忽略边界框的固有属性（如边界框的形状和尺寸）对边界框回归的影响。为了弥补现有研究的不足，本文提出了一种关注边界框自身形状和尺寸的边界框回归方法。首先，分析了边界框的回归特性，并发现边界框自身的形状和尺寸因素将对回归结果产生影响。基于上述结论提出了Shape IoU方法，该方法通过关注边界框自身的形状和尺寸来计算损失，从而使边界框回归更准确。最后，通过大量的比较实验验证了Shape-IoU方法，实验结果表明，Shape-IoU可以有效提高检测性能，并超越现有方法，在不同的检测任务中实现最先进的性能。

INTRODUCTION

????????目标检测是计算机视觉的基本任务之一，其目标是在图像中定位和识别物体。根据是否生成 Anchor 点，可以将方法分为Anchor-based的方法和Anchor-free的方法。Anchor-based的方法包括Faster R-CNN, YOLO系列,SSD 和RetinaNet。Anchor-free的方法包括CornerNet,CenterNet和FCOS。在这些检测器中，边界框回归损失函数作为局部化分支的重要组件起着不可替代的作用。

????????在目标检测领域，最常用的方法包括IoU,GIoU,CIoU,SIoU,等。IoU作为目标检测领域最广泛使用的损失函数，其优点在于更准确地描述了预测框和GT框之间的匹配程度。其缺点主要在于当两个框的交点为0时，无法准确描述预测框和GT框之间的位置关系。GIoU通过引入最小检测框来解决这个问题，从而提供了一个具体的改进。CIoU进一步提高了检测精度，通过在考虑预测框和GT框的中心点之间的归一化距离最小化的基础上，增加了一个形状损失项。在SIoU的工作中，提出将连接预测框中心点和GT框中心点的线的角大小作为新的损失项来考虑，以更准确地通过角的变化来判断预测框和GT框之间的匹配程度。

????????总之，边界框回归的主要方法是通过在IoU的基础上添加新的几何约束来使回归更准确。上述方法考虑了GT框和 Anchor 框的距离、形状和角度对边界框回归的影响，但忽略了边界框自身的形状和尺寸也会对边界框回归产生影响的事实。为了进一步提高回归的准确性，作者分析了边界框自身形状和角度的影响，并提出了一个新的边界回归损失：Shape-IoU。

本文的主要贡献如下：

1. 分析结果表明，在边界框回归过程中，边界框回归样本自身的形状和尺寸因素将对回归结果产生影响。

2. 基于现有的边界框回归损失函数，考虑到边界框回归样本自身的形状和尺寸对边界框回归的影响，提出了Shape-IoU损失函数，并在微型目标检测任务中提出了Shape-dot-distance和Shape-nwd损失。

3. 在各种检测任务上使用最先进的单阶段检测器进行了系列的比较实验，实验结果表明，本文提出的方法的检测效果优于现有方法，达到了最先进的水平。

RELATED WORK

A. IoU-based Metric in Object Detection

近年来，随着检测器的不断发展，边界框回归损失也得到了快速的发展。最初，IoU被提出用于评估边界框回归的状态，而基于IoU的DIoU, CIoU, EIoU, SIoU等方法则通过在IoU的基础上添加不同的约束来实现更好的检测。

1）IoU Metric：IoU是最流行的目标检测评估指标，定义如下：

其中，和分别表示预测框和GT框。

2) GIoU Metric:由于在边界框回归中，GT框和 Anchor 框之间没有重叠，导致IoU损失出现梯度消失的问题，因此提出了GIoU（广义IoU）来解决这个问题。其定义如下：

其中，表示GT框和 Anchor 框之间的最小检测框。

3) DIoU Metric:?与GIoU相比，DIoU考虑了边界框之间的距离约束，并在IoU的基础上添加了中心点归一化距离损失项，从而使得回归结果更准确。其定义如下：

在这里，和分别表示 Anchor 框的中心点和GT框的中心点，表示欧几里得距离，其中表示和之间的最小检测框的斜边长度。

CIoU进一步考虑了GT和 Anchor 框之间的形状相似性，通过在DIoU的基础上添加一个新的形状损失项来减少 Anchor 框和GT框之间的宽高比差异。其定义如下：

?在这里，和分别表示GT框的宽度和高度，和分别表示 Anchor 框的宽度和高度。

4)?EIoU Metric:EIoU根据CIoU重新定义了形状损失，并进一步通过直接减小GT框和 Anchor 框之间的宽高比来提高检测精度。其定义如下：

在这里，和分别表示最小检测框覆盖GT框和 Anchor 框的宽度和高度。

5)SIoU Metric：在前人研究的基础上，SIoU进一步考虑了边界框之间的角度对边界框回归的影响，旨在通过减小 Anchor 框和GT框之间的角度（水平或垂直方向）来加速收敛过程。其定义如下：

B. Metric in Tiny Object Detection

基于IoU的指标适用于一般的目标检测任务，对于小目标的检测，点距离（Dot Distance）和Normalized Wasserstein Distance（NWD）被提出来以克服它们对IoU值的敏感性。

1）?Dot Distance：

在这里，D表示GT框中心点与 Anchor 框中心点之间的欧几里得距离，S表示数据集中目标的平均大小，M表示图像的数量，表示第i张图像中的标注边界框数量，和分别表示第i张图像中第j个边界框的宽度和高度。

2)Normalized Gaussian Wasserstein Distance:

?在这里，权重w=2，C是与数据集相关的常数。

METHODS

A. Analysis of Bounding Box Regression Characteristics

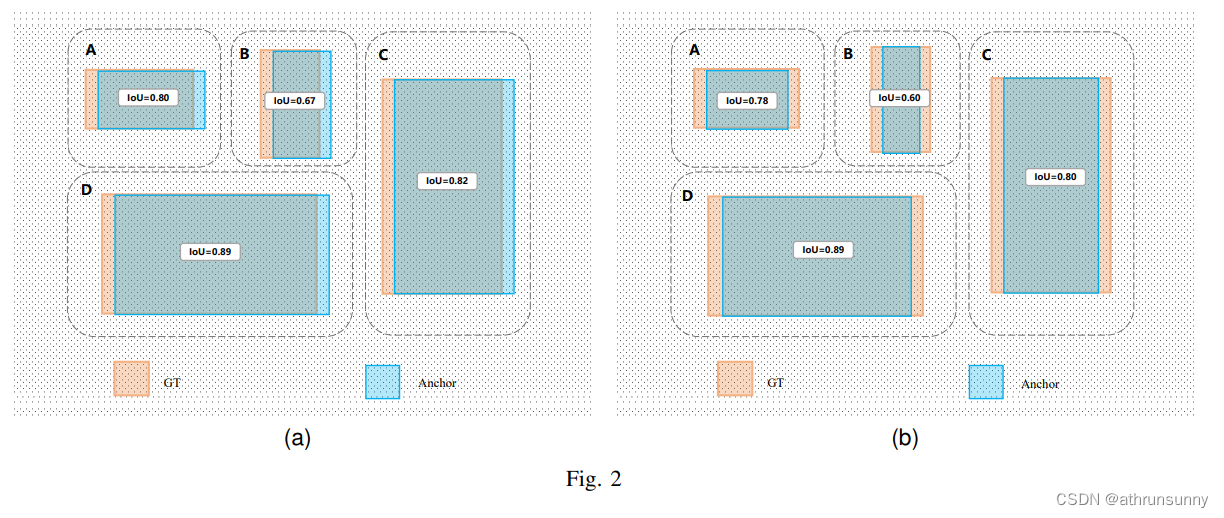
如图2所示，边界框回归样本A和B中的GT框的尺寸相同，而C和D中的GT框的尺寸相同。A和D中的GT框的形状相同，而B和C中的GT框的形状相同。C和D中边界框的尺寸大于A和B中边界框的尺寸。在图2a中，所有边界框回归样本的偏差相同，形状偏差为0。图2a和图2b之间的区别在于，图2b中所有边界框回归样本的形状偏差相同，为0。

在图2a中，A和B之间的偏差相同，但是IoU值存在差异。

在图2a中，C和D之间的偏差相同，但是IoU值存在差异，与A和B相比，IoU值的差异并不显著。

在图2b中，A和B的形状偏差相同，但是IoU值存在差异。

在图2b中，C和D的形状偏差相同，但是IoU值存在差异，与图2a中的A和B相比，IoU值的差异并不显著。

在图2a中，A和B之间的IoU值差异的原因在于它们的GT框有不同的形状，偏差（deviation）方向分别对应长边和短边，对A来说，GT框长边方向的偏差对IoU值的影响较小，而对于B来说，短边方向的偏差对IoU值的影响较大。

与large scale边界框相比，smaller scale边界框对IoU值的变化更加敏感，GT框的形状对smaller scale边界框的IoU值有更大的影响。因为A和B的scale比C和D小，所以在形状和偏差相同时，IoU值的差异更加显著。

类似地，从形状偏差的视角分析边界框回归，可以发现回归样本中GT框的形状会影响其IoU值在回归过程中的变化。

根据以上的分析，可以得出以下结论：

1、假设GT框并非正方形，其GT框存在长边与短边，对于deviation与shape-deviation相同且不全为0的情况下，回归样本中边框形状与尺度的差异会导致其IoU值存在差异。

2、对于相同尺度的边框回归样本，当回归样本deviation与shape-deviation相同且不全为0，边框的形状会对回归样本的IoU值产生影响，沿着其边框短边方向的deviation和shape-deviation所对应IoU值变化更为显著。

3、对于形状相同边框回归样本，当回归样本deviation与shape-deviation相同且不全为0，相较于较大尺度回归样本，较小尺度边框回归样本IoU值受GT框形状影响更为显著。

B. Shape-IoU

shape-iou如图3所示

?

其中，scale是缩放因子，与数据集中目标的大小相关，和分别表示水平方向和垂直方向上的权重系数，其值与GT框的形状有关。相应的边界框回归损失如下：?

C. Shape-IoU in Small Target

1) Shape-Dot Distance:将Shape-IoU的思想融入到点距离（Dot Distance）中，得到Shape-Dot Distance，其定义如下：

?2) Shape-NWD:同样地，将Shape-IoU的思想融入到归一化Normalized Wasserstein Distance（NWD）中，得到Shape-NWD，其定义如下：

EXPERIMENTS

A. PASCAL VOC on YOLOv8 and YOLOv7

PASCAL VOC数据集是目标检测领域最流行的数据集之一。在本篇文章中使用VOC2007和VOC2012的训练集（包括16551张图像）和测试集（包括4952张图像），来对YOLOv8和YOLOv7-tiny进行比较实验，并选择SIoU作为实验的比较方法。

实验结果如表I所示：

B. VisDrone2019 on YOLOv8

VisDrone2019是目标检测领域最流行的无人机航空图像数据集，其中包含比一般数据集更多的较小目标。在本实验中，选择YOLOv8作为检测器，并采用SIoU作为比较方法。

实验结果如下：

C. AI-TOD on YOLOv5

AI-TOD是一个遥感图像数据集，与一般数据集不同，它包含大量微小目标，且目标平均大小为12.8像素。在本实验中，选择YOLOv5s作为检测器，并采用SIoU作为比较方法。

实验结果如下：

Code

def shape_iou(box1, box2, xywh=True, scale=0  eps=1e-7):
    (x1, y1, w1, h1), (x2, y2, w2, h2) = box1.chunk(4, -1), box2.chunk(4, -1)
    w1_, h1_, w2_, h2_ = w1 / 2, h1 / 2, w2 / 2, h2 / 2
    b1_x1, b1_x2, b1_y1, b1_y2 = x1 - w1_, x1 + w1_, y1 - h1_, y1 + h1_
    b2_x1, b2_x2, b2_y1, b2_y2 = x2 - w2_, x2 + w2_, y2 - h2_, y2 + h2_

    # Intersection area
    inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \
            (torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)

    # Union Area
    union = w1 * h1 + w2 * h2 - inter + eps

    # IoU
    iou = inter / union

    #Shape-Distance    #Shape-Distance    #Shape-Distance    #Shape-Distance    #Shape-Distance    #Shape-Distance    #Shape-Distance  
    ww = 2 * torch.pow(w2, scale) / (torch.pow(w2, scale) + torch.pow(h2, scale))
    hh = 2 * torch.pow(h2, scale) / (torch.pow(w2, scale) + torch.pow(h2, scale))
    cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1)  # convex width
    ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1)  # convex height
    c2 = cw ** 2 + ch ** 2 + eps                            # convex diagonal squared
    center_distance_x = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2) / 4
    center_distance_y = ((b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4
    center_distance = hh * center_distance_x + ww * center_distance_y
    distance = center_distance / c2

    #Shape-Shape    #Shape-Shape    #Shape-Shape    #Shape-Shape    #Shape-Shape    #Shape-Shape    #Shape-Shape    #Shape-Shape    
    omiga_w = hh * torch.abs(w1 - w2) / torch.max(w1, w2)
    omiga_h = ww * torch.abs(h1 - h2) / torch.max(h1, h2)
    shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), 4) + torch.pow(1 - torch.exp(-1 * omiga_h), 4)
    
    #Shape-IoU    #Shape-IoU    #Shape-IoU    #Shape-IoU    #Shape-IoU    #Shape-IoU    #Shape-IoU    #Shape-IoU    #Shape-IoU
    iou = iou - distance - 0.5 * ( shape_cost)
    return iou  # IoU