Leetcode 47 全排列 II
发布时间:2023年12月17日
题意理解:
? ? ? ? 首先理解全排列是什么?全排列:使用集合中所有元素按照不同元素进行排列,将所有的排列结果的集合称为全排列。
? ? ? ? 这里的全排列难度升级了,问题在于集合中的元素是可以重复的。
? ? ? ? 问题:相同的元素会导致排列重复,需要对结果进行去重操作。
? ? ? ? 难点:如何去重?
解题思路:
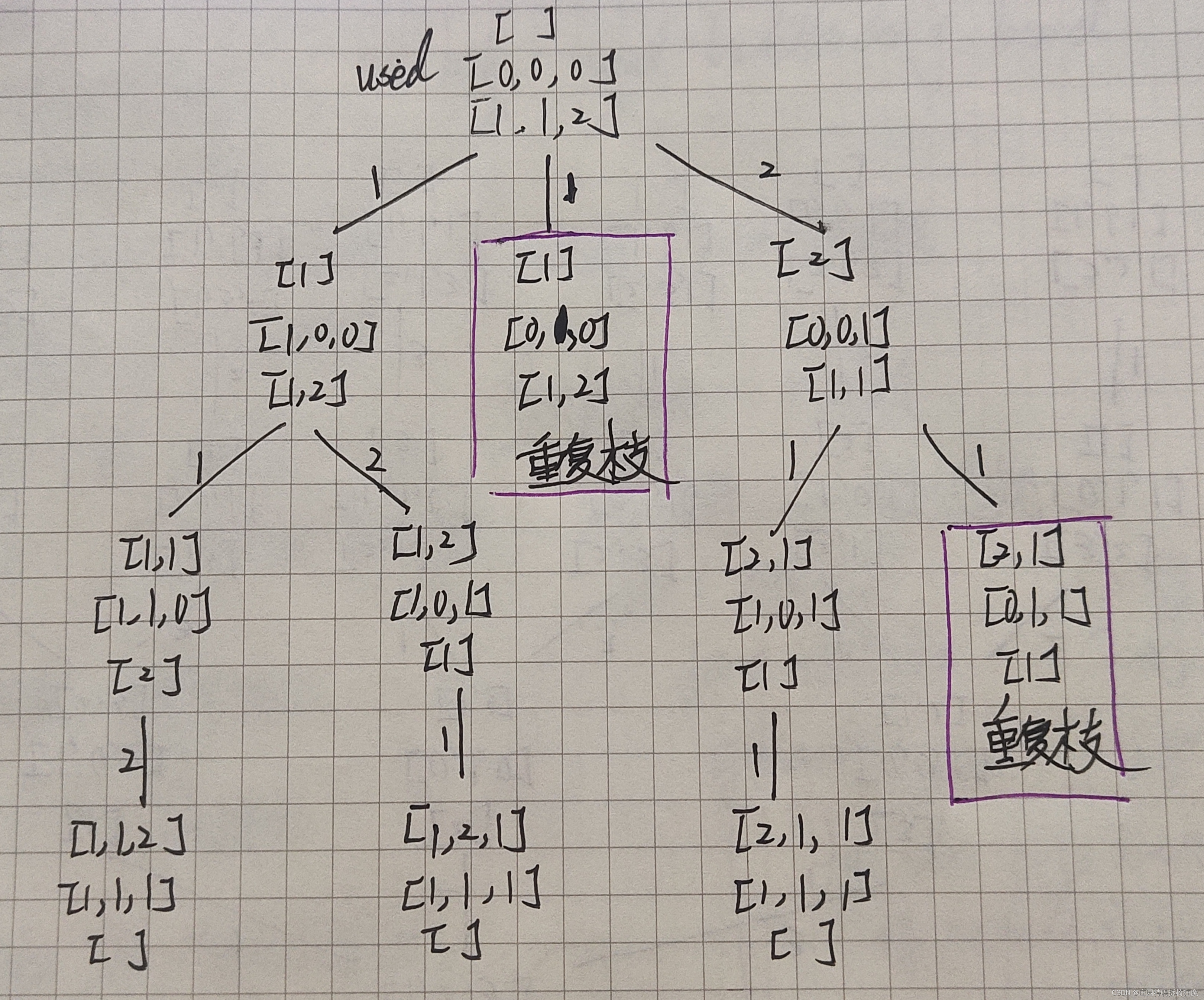
? ? ? ? 排列可以用回溯方法来进行解决。可以将其解决方案抽象为一棵树结构。
????????我们可以发现:
? ? ? ? ? ? ? ? 当前枝当前层,选择到重复的元素时,后出现两个相同的树枝结构,造成相同的相同的重复的结果,所以去重应该剪枝:当前枝当前层重复元素的选择。——树层去重。
? ? ? ? 为了实现树层去重:我们维护一个used[]数组来记录元素的访问状态。
? ? ? ? used数组的作用:????????
? ? ? ? ? ? ? ? 保证所有元素只是用一次。
? ? ? ? ? ? ? ? 来辅助树层去重操作。
1.暴力回溯+剪枝优化
回溯解决问题的三个关键步骤:
? ? ? ? 确定返回值和参数列表
? ? ? ? 确定终止条件
? ? ? ? 确定单层递归逻辑:1.保证元素只用一次? 2.树层剪枝,防止重复值造成结果重复。
List<List<Integer>> result=new ArrayList<>();
LinkedList<Integer> path=new LinkedList<>();
boolean[] used=null;
public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);
used=new boolean[nums.length];//初始化默认值false
backtracking(nums);
return result;
}
public void backtracking(int[] nums){
//确定终止条件
if(path.size()== nums.length){
result.add(new ArrayList<>(path));
return;
}
//单层递归逻辑
for(int i=0;i<nums.length;i++){
if(used[i]==true) continue;//该元素用过
if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false) continue;//同枝同层剪枝
path.add(nums[i]);
used[i]=true;
backtracking(nums);
path.removeLast();
used[i]=false;
}
}2.分析
时间复杂度:O(n×n!)
空间复杂度:O(n)
文章来源:https://blog.csdn.net/lt_BeiMo/article/details/134978960
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 使用tailscale访问对端局域网上的其他设备
- Everything结合内网穿透搭建在线资料库并实现随时随地远程访问
- 微信服务号和订阅号区别
- MySQL和 Oracle查看表信息
- S7-1200/1500(T) 通过功能块FB38051实现 SINAMICS S200 的 EPOS 基本定位控制
- sql:最后一个进入电梯的人
- Java研学-Servlet3.0文件上传下载
- TCP/IP详解——UDP 协议
- 带你解析Git的基础功能(三)
- 计算机组成原理-CPU数据通路(单总线结构和专用通路结构)