第 376 场 LeetCode 周赛题解
A 找出缺失和重复的数字

模拟
class Solution {
public:
vector<int> findMissingAndRepeatedValues(vector<vector<int>> &grid) {
int n = grid.size();
vector<int> vis(n * n + 1);
for (auto &r: grid)
for (auto &c: r)
vis[c]++;
vector<int> res(2);
for (int i = 1; i <= n * n; i++)
if (vis[i] == 2)
res[0] = i;
else if (vis[i] == 0)
res[1] = i;
return res;
}
};
B 划分数组并满足最大差限制

贪心:为了使组内元素之差尽可能小,所以只将排序后相邻的三个元素依次划分为一个子数组
class Solution {
public:
vector<vector<int>> divideArray(vector<int> &nums, int k) {
sort(nums.begin(), nums.end());
vector<vector<int>> res;
for (int i = 0; i < nums.size(); i += 3)
if (nums[i + 2] - nums[i] > k)
return {};
else {
res.push_back({nums[i], nums[i + 1], nums[i + 2]});
}
return res;
}
};
C 使数组成为等数数组的最小代价

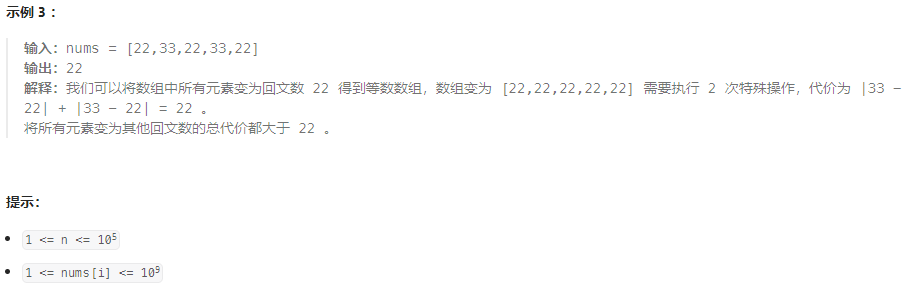
枚举:首先对 n u m s nums nums 排序,若 n u m s nums nums 的中位数 m i d mid mid 为回文数则将 n u m s nums nums 中各元素变为 m i d mid mid 即可产生最小代价,否则 y y y 应该是小于 m i d mid mid 的且最接近 m i d mid mid 的回文数 或 大于 m i d mid mid 的且最接近 m i d mid mid 的回文数
class Solution {
public:
using ll = long long;
bool ispow10(int x) {
while (x % 10 == 0)
x /= 10;
return x == 1;
}
vector<int> find_val(int x) {//找到最接近x的几个回文数
vector<int> res;
string s = to_string(x);
if (ispow10(x)) {
if (x == 1e9)
return {(int) 1e9 - 1};
else if (x == 1)
return {x};
else
return {x + 1, x - 1};
} else if (ispow10(x + 1) || ispow10(x - 1))
return {x};
if (s.size() % 2 == 0) {
string left = s.substr(0, s.size() / 2);
vector<int> d{1, 0, -1};
for (auto di: d) {
string nleft = to_string(stol(left) + di);
string r = string(nleft.rbegin(), nleft.rend());
ll t = stol(nleft + r);
if (t < 1e9) {
res.push_back(t);
}
}
} else {
string left = s.substr(0, s.size() / 2 + 1);
vector<int> d{1, 0, -1};
for (auto di: d) {
string nleft = to_string(stol(left) + di);
string r = string(nleft.rbegin() + 1, nleft.rend());
ll t = stol(nleft + r);
if (t < 1e9) {
res.push_back(t);
}
}
}
return res;
}
long long minimumCost(vector<int> &nums) {
int n = nums.size();
sort(nums.begin(), nums.end());
int x = n % 2 == 0 ? (nums[(n - 1) / 2] + nums[n / 2]) / 2 : nums[n / 2];
auto tar = find_val(x);
ll res = INT64_MAX;
for (auto ti: tar) {
ll t = 0;
for (auto it: nums)
t += abs(it - ti);
res = min(res, t);
}
return res;
}
};
D 执行操作使频率分数最大

二分+枚举:二分答案 m i d mid mid,在排序后的 n u m s nums nums 中枚举长为 m i d mid mid 的子数组,判断该将该子数组变为同一元素的最少操作(变为该子数组的中位数即可产生最少操作数)数是否不超过 k k k
class Solution {
public:
using ll = long long;
int maxFrequencyScore(vector<int> &nums, long long k) {
int n = nums.size();
sort(nums.begin(), nums.end());
vector<ll> ps(n + 1);//前缀和
for (int i = 0; i < n; i++)
ps[i + 1] = ps[i] + nums[i];
int l = 1, r = n;
while (l < r) {
int mid = (l + r + 1) / 2;
int find = 0;
for (int l = 0, r = mid - 1; r < n; l++, r++) {//子数组nums[l,r]
int cen = (l + r) / 2;
int tar = nums[cen];//将子数组各元素变为tar产生最少操作数
ll t = 1LL * tar * (cen - l + 1) - (ps[cen + 1] - ps[l]) + ps[r + 1] - ps[cen + 1] - 1LL * tar * (r - cen);
if (k >= t) {
find = 1;
break;
}
}
if (find)
l = mid;
else
r = mid - 1;
}
return l;
}
};
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- mybatis练习
- 外包干了5个月,技术明显退步了...
- 自然语言处理2——轻松入门情感分析 - Python实战指南
- 初学者SkyWalking详细使用文档
- ElasticSearch自定义算分排序(Function Score Query)
- 肿瘤NGS产品IVD报证入门者的基础资料
- Qt: QSpliter
- 一款用于host碰撞而生的小工具
- YOLOV7剪枝流程
- 【运维知识大神篇】运维界的超神器Kubernetes教程4,事已至此,来一波实战吧!(整合项目进镜像+打包项目成镜像+将Docker项目上K8s集群)