代码随想录27期|Python|Day35|435. 无重叠区间|763.划分字母区间|56. 合并区间
发布时间:2024年01月22日
?435. 无重叠区间
和昨天的射爆气球是一样的处理方式:
由于不需要进行不重合的时候的计算,只需要对重合进行处理,所以反而更加简单。

1、按照区间左边界从小到大排序;
2、从索引1开始遍历,对于i-1的右边界大于i的左边界的情况,记录一次重合,并且修改i的右边界是i和i-1的最小值。
(需要注意lambda取出元组的方式和遍历的时候判断的边界)
class Solution(object):
def eraseOverlapIntervals(self, intervals):
"""
:type intervals: List[List[int]]
:rtype: int
"""
intervals.sort(key=lambda x: x[0])
res = 0
for i in range(1, len(intervals)):
if intervals[i-1][1] > intervals[i][0]:
res += 1
intervals[i][1] = min(intervals[i-1][1], intervals[i][1])
return res?763.划分字母区间?
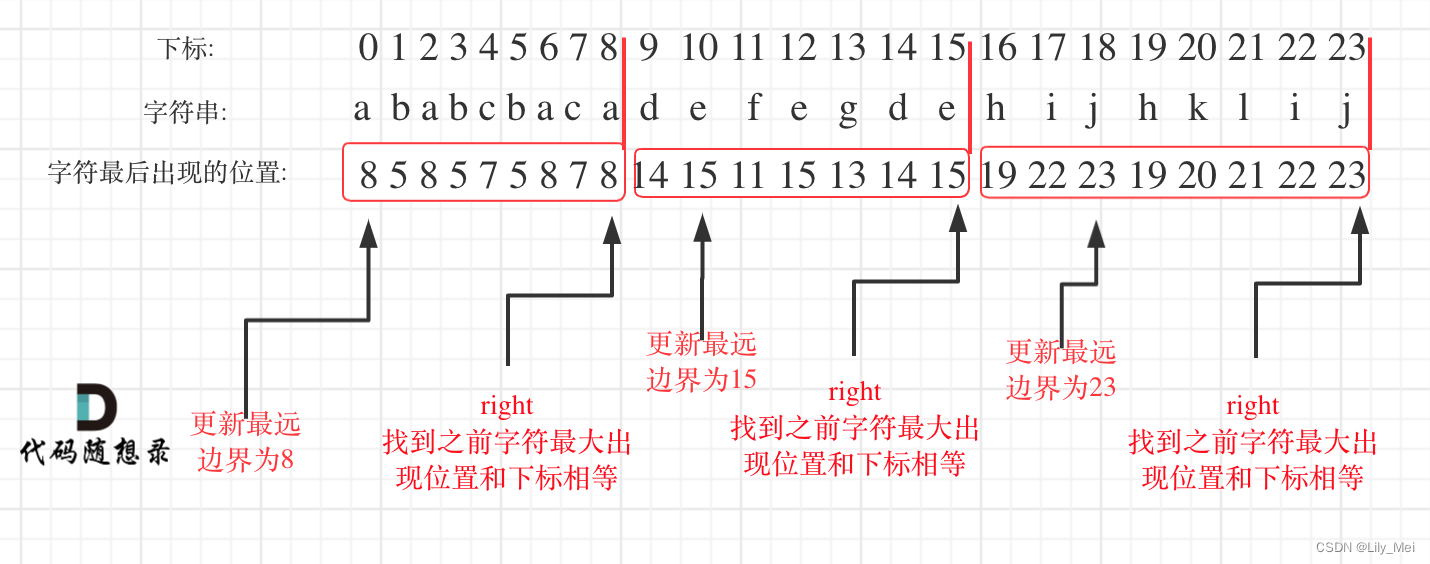
本题也是判断区间边界的一道题。
1、首先第一次遍历获取每个字母对应的最远距离;
2、第二次遍历不断更新右边界为当前遍历到的字母最远距离的最大值;
3、在遍历到右边界的时候,保存区间的长度,更新左边界。
class Solution(object):
def partitionLabels(self, s):
"""
:type s: str
:rtype: List[int]
"""
far_reach = {} # 创建哈希表用来储存每个字母对应的最远的距离
# 第一次遍历,获取每个字母对应的最远的距离
for i, char in enumerate(s):
far_reach[char] = i
res = []
left, right = 0, 0 # 声明左右边界,用来计算区间长度
# 第二次遍历,不断更新右边界的值,如果遍历到了右边界,储存区间长度
for i, char in enumerate(s):
right = max(right, far_reach[char])
if i == right:
res.append(right - left + 1)
left = i + 1
return res需要注意使用right和left双指针计算区间长度的方法,以及更新右边界的时候是取最大值。
?56. 合并区间
关键在于对于重合区间的处理,这里采用的是类似栈的方法,每次仅修改栈最后一个位置的右端点。
1、按照区间左边界从小到大排序;
2、先将第一个区间入栈;
3、遍历每一个区间:
? ? ? ? 1,如果重合,直接修改入栈的最后一个区间的右端点为右边界的最大值;
? ? ? ? 2,如果不重合,直接入栈。
class Solution(object):
def merge(self, intervals):
"""
:type intervals: List[List[int]]
:rtype: List[List[int]]
"""
intervals.sort(key=lambda x: x[0])
res = []
res.append(intervals[0]) # 储存第一个区间
for i in range(1, len(intervals)):
if res[-1][1] >= intervals[i][0]:
res[-1][1] = max(intervals[i][1], res[-1][1]) # 直接修改保存好的区间的右端点
else:
res.append(intervals[i]) # 不重合直接添加
return res第35天完结!!
文章来源:https://blog.csdn.net/m0_57527624/article/details/135748822
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 大模型背景下计算机视觉年终思考小结(一)
- 车载打气泵智能应用方案设计
- Python 常用技能手册
- 2023年程序员必须知道的10大代码网站!
- AI在广告中的应用——预测性定位和调整
- 分类预测 | Matlab实现WOA(海象)-XGboost分类【24年新算法】基于海象优化算法(WOA)优化XGBoost的数据分类预测
- 如何使用代理助手Proxy Helper插件管理海外proxy代理
- 简述 | OTG原理功能简述及解决方案
- IO第6天
- QMessageBox自定义按钮文本中文显示,按钮个数等