牛客周赛 Round 22(C、D题解)

C、小红的数组构造（思维）

一、题目要求

链接：登录—专业IT笔试面试备考平台_牛客网
来源：牛客网
?

题目描述

小红想让你构造一个长度为 n?的数组，满足以下三个条件：
1. 该数组最大值不超过 k。
2. 该数组所有数都不相同。
3. 数组所有数之和等于 x。

输入描述:

输入一行三个正整数 n,k,x，用空格隔开。
1≤n≤10^5
1≤k≤x≤10^14

输出描述:

如果无法构造，请输出-1。
否则输出 n 个正整数，用空格隔开，代表构造的数组。有多解时输出任意即可。

示例1

输入

4 6 15

输出

1 3 6 5

示例2

输入

2 2 2

输出

-1

说明

显然无法构造出两个不相等的正整数和为2。

二、思路

1.先初始化数组

for(i=1;i<=n;i++)
   a[i]=i;
   x=x-i;

2.判断

（1）当有n个不同的数的时候，此时若从1开始，则最大值为n，当n比给定的k要大的时候则不符合条件

（2）当x<0的时候，则说明（1+n）*n/2 大于x，也不符合条件

3.倒着循环找差值，并将差值加到相应的数组中

4.如果经过3操作后，x等于0，则说明新创造的数组符合条件，当x!=0的时候，则说明不符合条件。

三、代码

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
const int N=2e5+10;
const int inf=0x3f3f3f3f;
int n,k,x;
int a[N];
void solve()
{
	cin>>n>>k>>x;
	int i,j;
	for(i=1;i<=n;i++)
	{
		a[i]=i;
		x=x-i;
	}
	if(x<0||n>k)
	{
		cout<<"-1"<<endl;
		return;
	}
	for(i=n;i>=1;i--)
	{
		int y=min(x,k-a[i]);
		if(y<0)
		   y=0;
		x-=y;
		a[i]+=y;
		k=a[i]-1;
	}
	if(x!=0)
	{
		cout<<"-1"<<endl;
		return ;
	}
	for(i=1;i<=n;i++)
	{
		cout<<a[i]<<' '; 
	}
	cout<<endl;
}
signed main()
{
	IOS;
    int t=1;
    while(t--)
    {
       solve();
    }
    return 0;
}

D、小红的图上删边（并查集）

一、题目要求

链接：登录—专业IT笔试面试备考平台_牛客网
来源：牛客网
?

题目描述

小红拿到了一个n个节点、m条边的无向连通图，每个节点的权值已知。
小红删掉一条边时，可以获得连接该边的两个节点“权值乘积末尾0数量”的价值。例如，一条边连接的两个点权值是50和60，那么小红删掉这条边获得的价值为3。
小红想知道，在保证这张图连通的情况下，最多可以通过删边获得多少价值？

输入描述:

第一行输入两个正整数 n 和 m，代表图的点数和边数。
第二行输入 n个正整数 aii，代表每个点的权值。
接下来的 m 行，每行输入两个正整数 u 和 v，代表点 u 和点 v 有一条边连接。
保证图连通，且无重边，无自环。
2≤n≤10^5
n?1≤m≤min(10^5,n?(n?1)2)
1≤ai≤10^14
1≤u,v≤n

输出描述:

一个整数，代表删边可以获得的最大价值。

示例1

输入

3 3
5 8 25
1 2
2 3
1 3

输出

2

说明

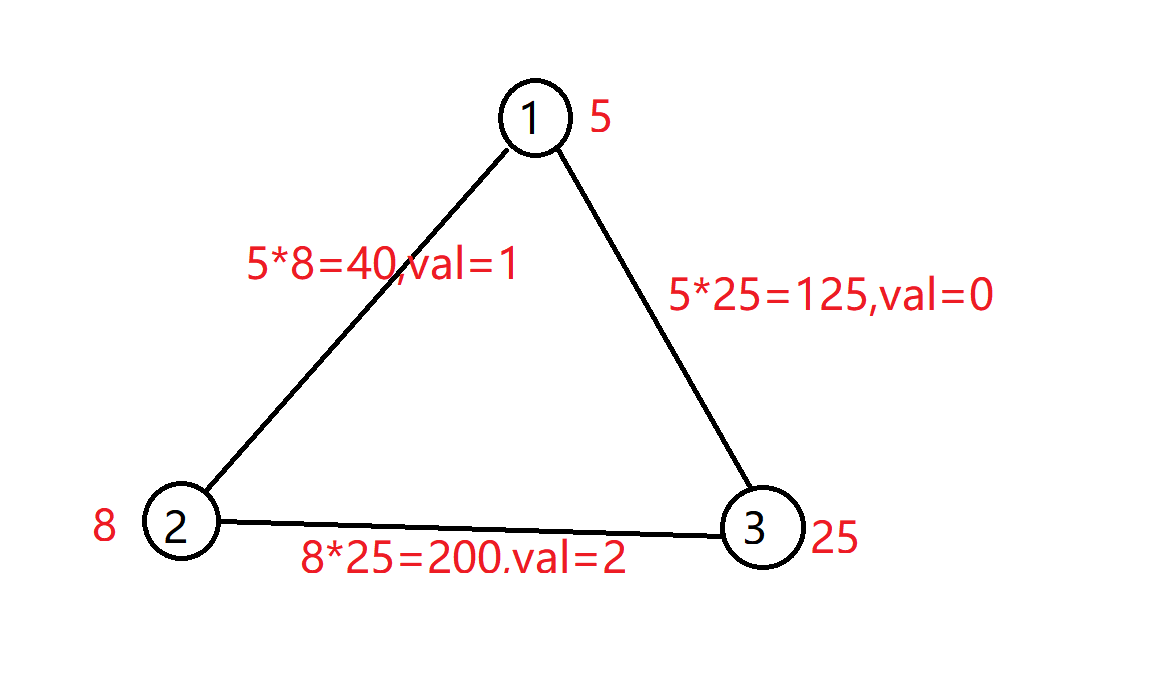
删掉第二条边，由于8*25=200，末尾有2个零，所以可以获得2的价值。

二、思路

1.创建结构体u,v,w;
即：从u到v的权值为w
2.利用while()求出2的个数和5的个数，取两者最小值，则为w的值；
累加所有w的值则为cnt;?
3. 对结构体里面的w从小到大排序，初始化并查集，利用find()函数，
在合并的过程中，累加w的值为s,当合并的个数为n-1的时候，跳出即可
4.则通过删边，获得的最大价值为 cnt-s?

三、代码

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
const int N=2e5+10;
const int inf=0x3f3f3f3f;
int n,m;
int fa[N],a[N];
struct node
{
	int  u,v,w;
}q[N];
bool cmp(node l,node r)
{
	return l.w<r.w;
}
int find(int x)
{
	if(fa[x]==x)
	    return x;
	return fa[x]=find(fa[x]);
} 
void solve()
{
	cin>>n>>m;
	int i,j;
	int cnt=0;
	for(i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	for(i=1;i<=m;i++)
	{
		cin>>q[i].u>>q[i].v;
		int sum1=0,sum2=0;
		int cc=a[q[i].u];
		while(cc%2==0) sum1++,cc/=2;
		while(cc%5==0) sum2++,cc/=5;
		int bb=a[q[i].v];
		while(bb%2==0) sum1++,bb/=2;
		while(bb%5==0) sum2++,bb/=5;
		q[i].w=min(sum1,sum2);//取2和5个数的最小值，即0的个数 
		cnt+=q[i].w;
	}
	sort(q+1,q+m+1,cmp);
	for(i=1;i<=n;i++)//并查集：初始化 
	{
		fa[i]=i;
	} 
	int cntt=0,s=0;
	for(i=1;i<=m;i++)
	{
		if(find(q[i].u)!=find(q[i].v))
		{
			fa[find(q[i].u)]=find(q[i].v);
			s+=q[i].w;
			cntt++;
		}
		if(cntt==n-1)
		   break;
	} 
	cout<<cnt-s<<endl;
}
signed main()
{
    int t=1;
    while(t--)
    {
       solve();
    }
    return 0;
}