【数字电路】期末速通!
1. 数制及转换
常用的数制:十进制(D),二进制(B),八进制(O),十六进制(H)。
常见的码制包括以下几种:
- 二进制码(Binary Code):使用0和1两个数字来表示信息。
- 十进制码(Decimal Code):使用0至9十个数字来表示信息。
- 格雷码(Gray Code):通过保证相邻码字只有一位变化,降低误码率。
- ASCII码(American Standard Code for Information Interchange):使用7位二进制数来表示英文字母、数字、标点符号和控制字符。
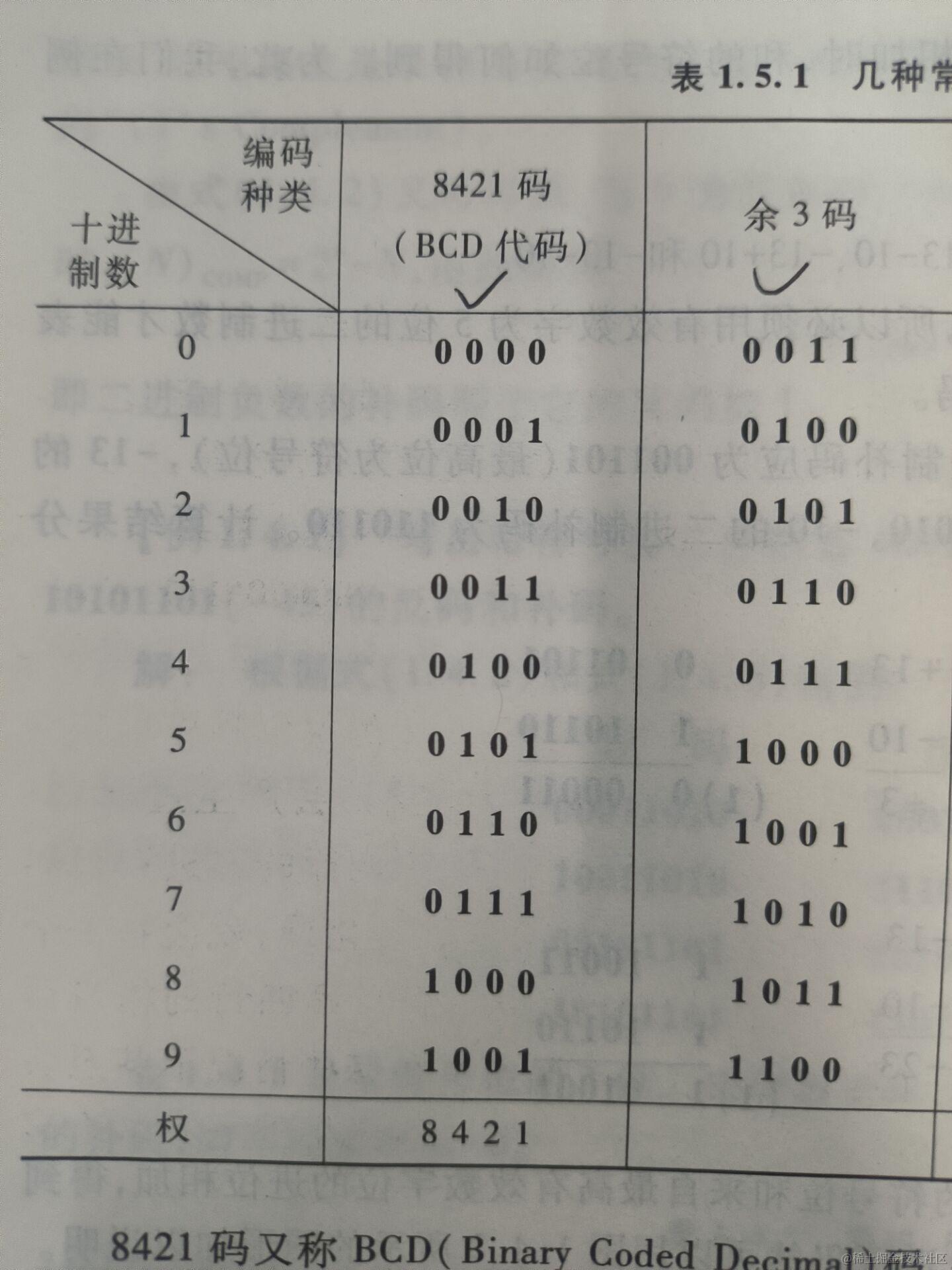
- BCD码(Binary Coded Decimal)(又称为 8421 码):使用4位二进制数来表示0至9十个数字,常用于数码显示器。
- 余三码(Excess-3 Code):采用8421BCD码的基础上加上3,用于表示十进制数。

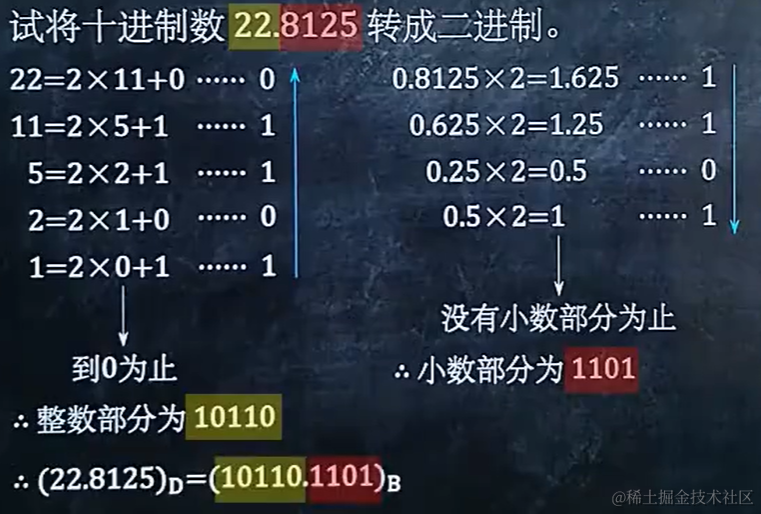
1.1 将二进制转成十进制

1.2 将十进制转成二进制
1.3 将二进制转成八进制

1.4 将八进制转成二进制

1.5 将二进制转成十六进制

1.6 将十六进制转成二进制


2. 逻辑门电路
0 表示开关断开,1 表示开关闭合。
2.1 给出逻辑图,判断数字
同或:相同就是 1。

2.2 给出逻辑图,写出函数表达式
非有多种表示方法,见P(22)。
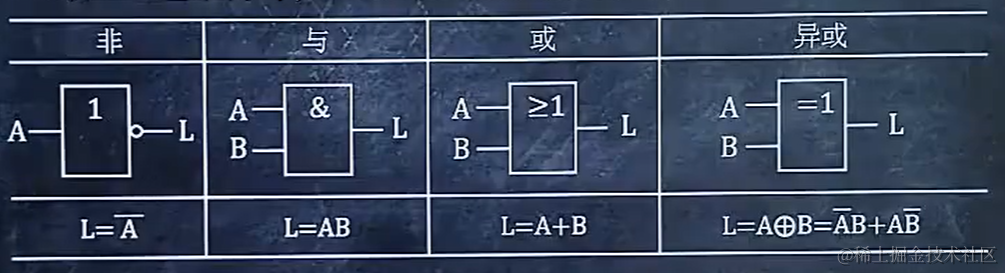
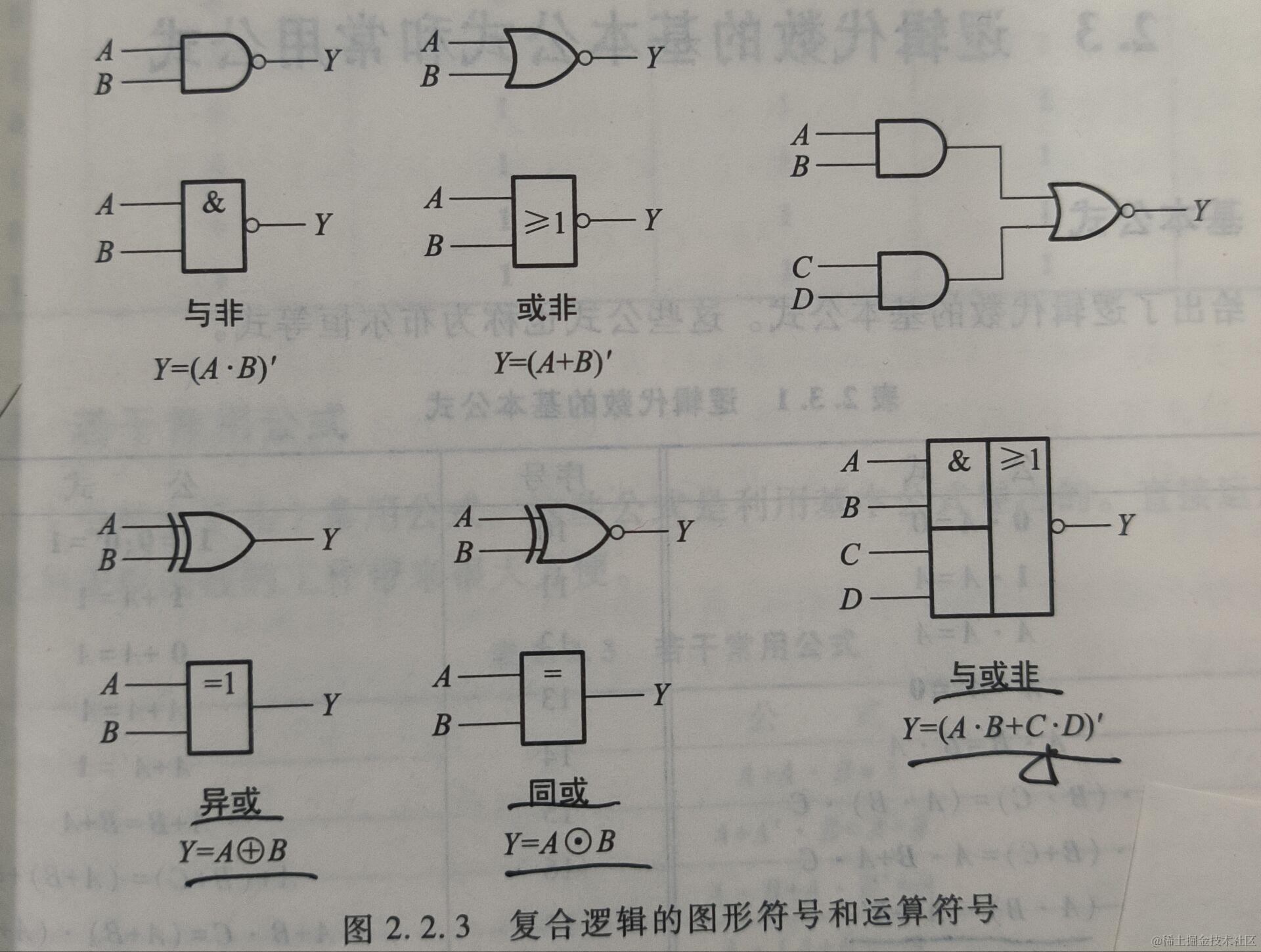

2.3 给出逻函数表达式,画出逻辑图
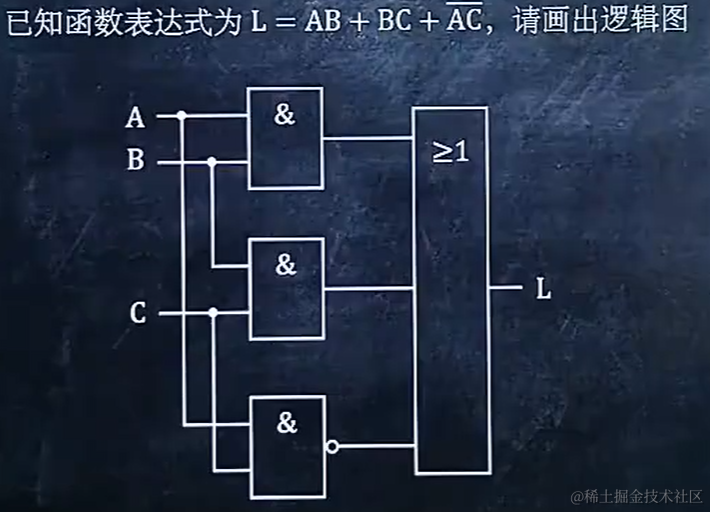
复合门电路及其逻辑功能:
- 与非门:该门包含两个输入和一个输出。当且仅当所有输入都为高电平时,输出为低电平。它可以实现与门、或门、非门以及其他逻辑功能。
- 或非门:该门也包含两个输入和一个输出。当且仅当所有输入都为低电平时,输出为高电平。它可以实现与门、或门、非门以及其他逻辑功能。
- 异或门:该门包含两个输入和一个输出。当且仅当输入的电平不相同时,输出为高电平。它可以实现比较、加法以及其他逻辑功能。
- 与或非门:该门包含多个输入和一个输出。它可以实现与非门、或非门、与门和非门的组合逻辑功能。
- 或与非门:该门也包含多个输入和一个输出。它可以实现或非门、与非门、或门和非门的组合逻辑功能。
3. 化简逻辑表达式
常见的逻辑函数表示方法:
-
逻辑真值表:真值表是逻辑函数的一种最直观的表示方法。它列出了函数的所有可能输入组合以及对应的输出结果。
-
布尔表达式(Boolean Expression):布尔表达式使用逻辑运算符(与、或、非)和变量(常用字母表示)来表示逻辑函数。例如,使用AND、OR、NOT运算符以及变量A、B来表示逻辑与函数为A AND B。类似于逻辑函数式(Y=A(B+C))。
-
卡诺图:卡诺图是一种图形化的方法,用于简化逻辑函数的布尔表达式。它将函数的真值表转化为一个矩形的表格,通过合并相邻的1来最小化表达式。化简法:卡诺图的构成、卡诺圈原则、无关项的表示及其应用。
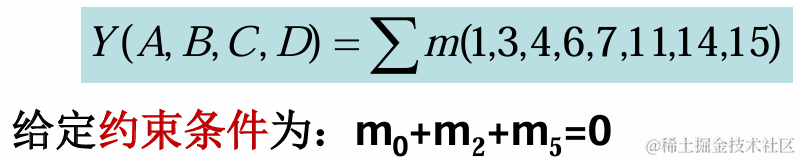
-
逻辑图:逻辑图使用逻辑门和连线来表示逻辑函数。它以图形方式显示了逻辑电路的组成和信号流动。
-
波形图。
这些表示方法在不同的应用场景中有着不同的优势和使用方法。根据情况选择适合的表示方法可以更方便地理解和设计逻辑函数。如果还有其他问题,请随时提问。
3.1 将卡诺图表示成逻辑表达式

3.2 将逻辑表达式画进卡诺图
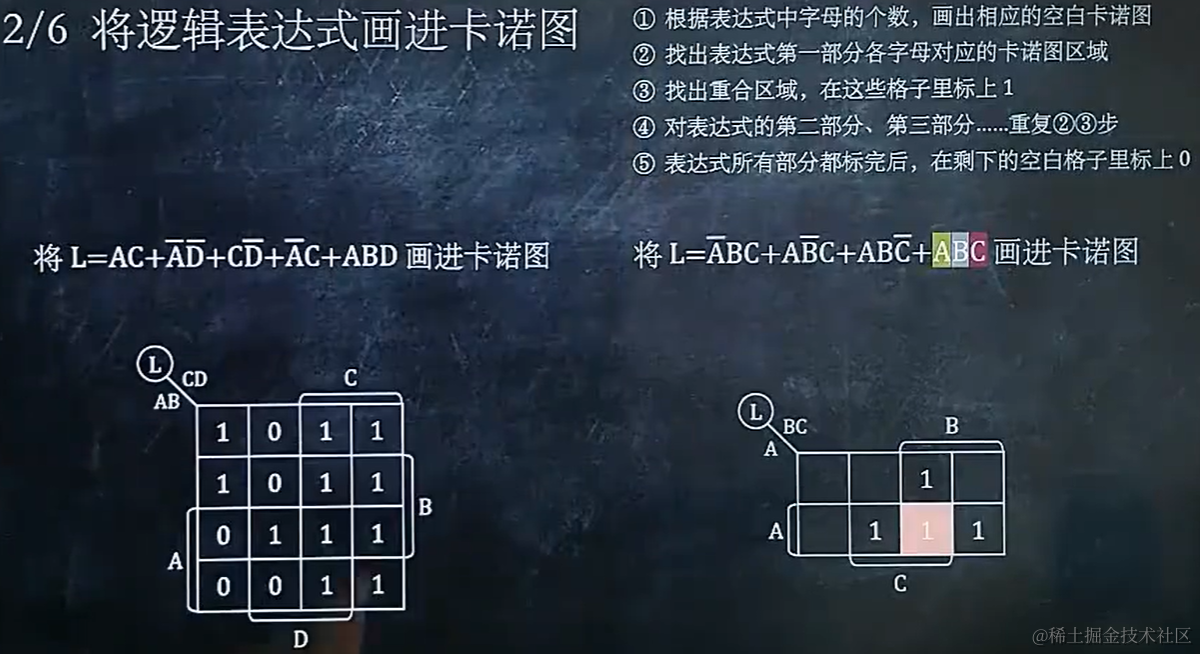
3.3 用卡诺图化简逻辑表达式
就是题型二和题型一的结合。
3.4 用公式法化简逻辑表达式
德摩根定理(反演律)。
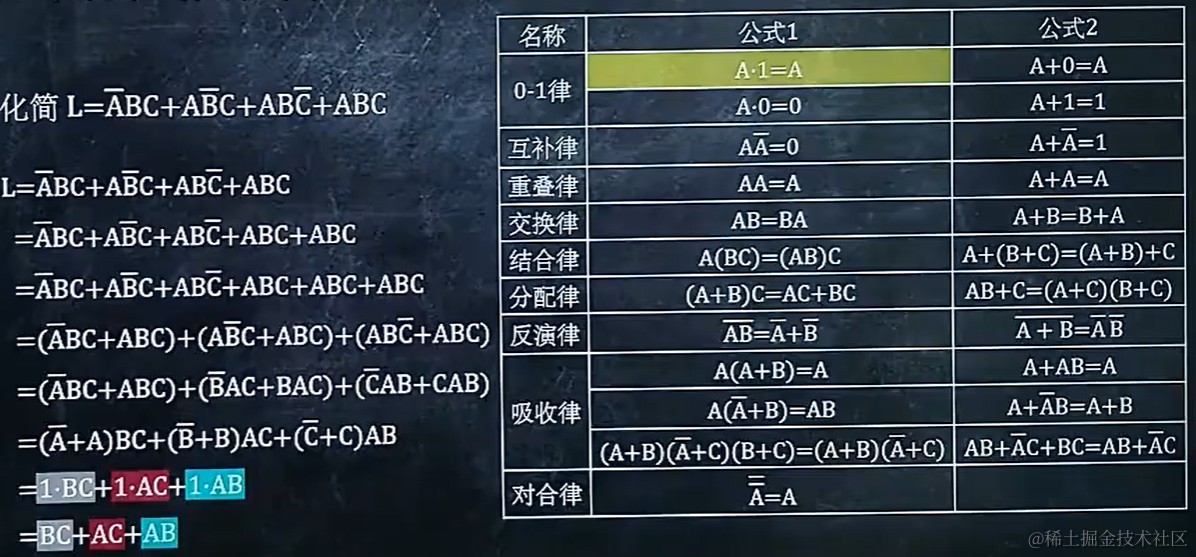

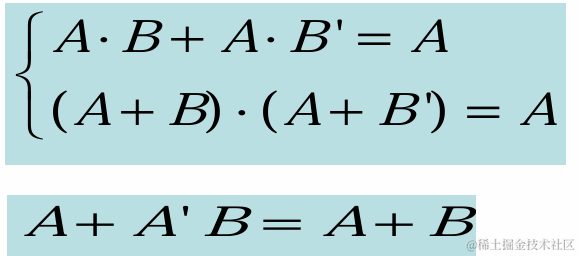
3.5 求反函数

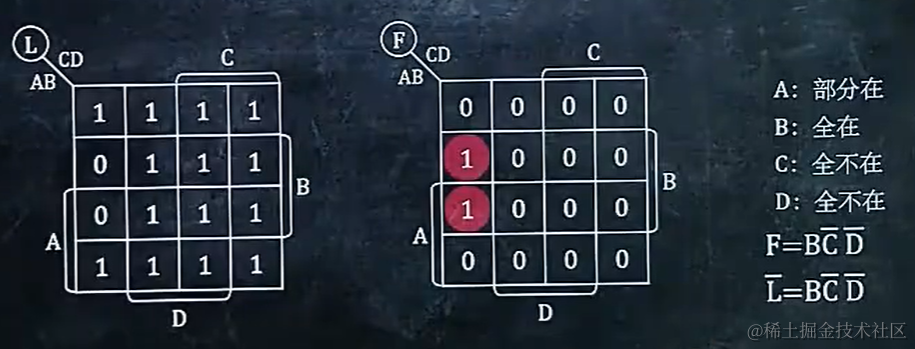
3.6 求卡诺图表示函数的反函数
法一:先用卡诺图求出逻辑表达式,然后求反函数
法二:卡诺图的0和1互换,求逻辑表达式
4. 组合逻辑电路的分析与设计
4.1 给出逻辑电路图,分析逻辑功能
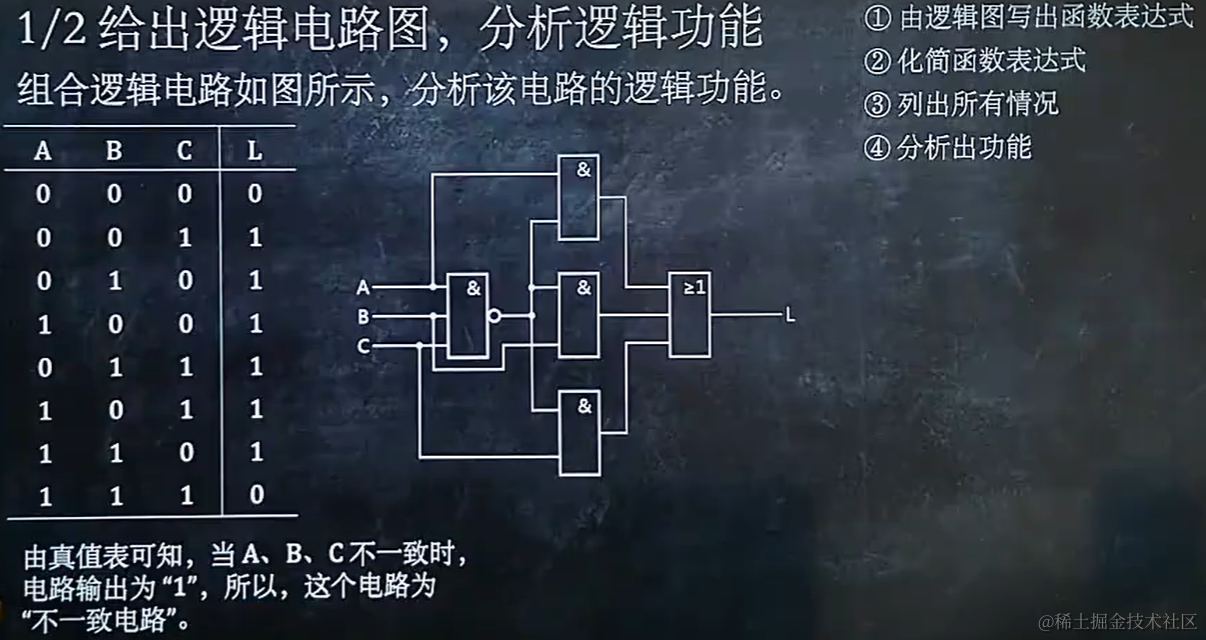
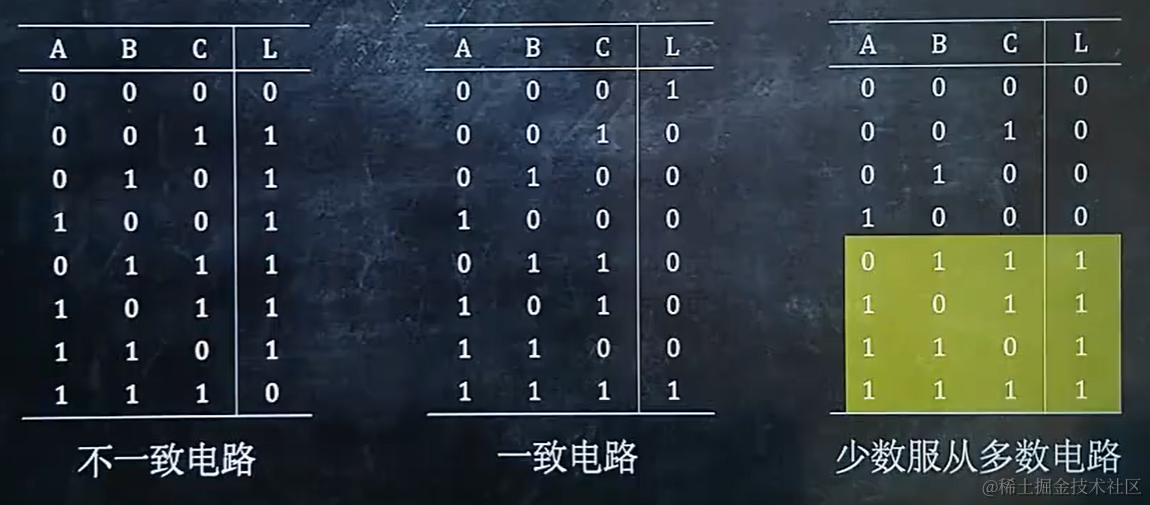
4.2 给出功能要求,设计电路
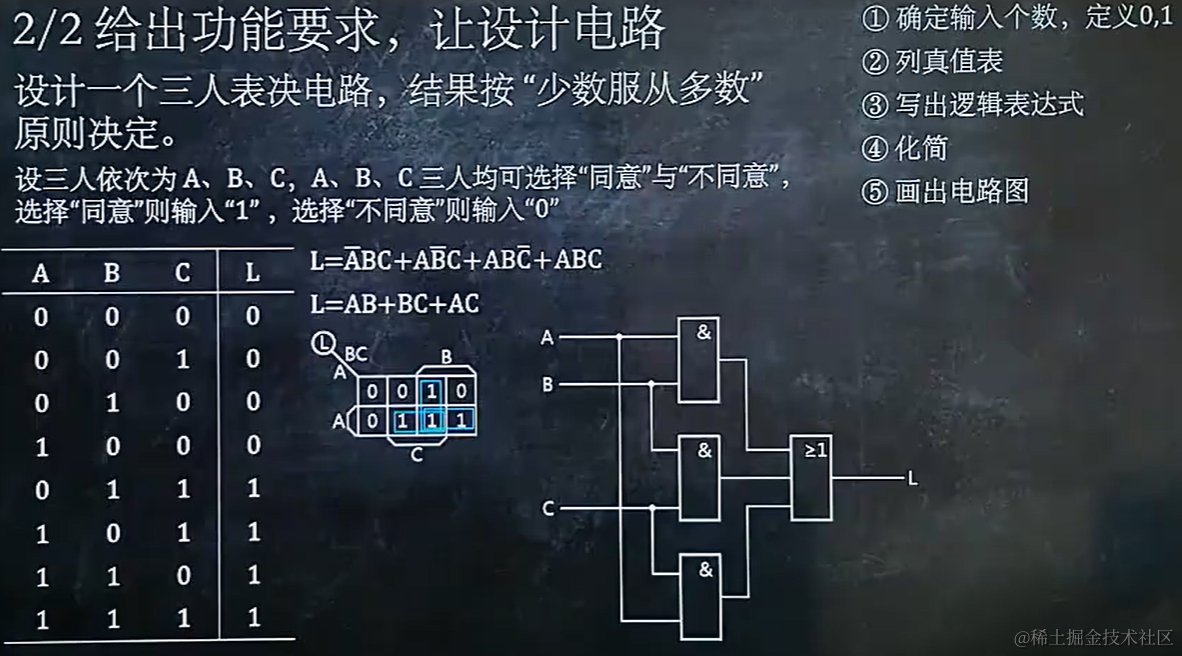
5. 最小项
最小项是布尔函数的基本构成单元之一,具有一些重要的性质,包括:
-
每个输入组合都有唯一一个最小项与之对应:对于 n 个变量的布尔函数,共有 2^n 个可能的输入组合,每个输入组合都对应一个唯一的最小项。
-
最小项的长度等于输入变量的个数:最小项的长度(即字长)等于布尔函数的输入变量的个数。
-
最小项的限制:最小项的取值要么为0,要么为1,不能同时为0和1。
-
最小项与真值表的对应关系:最小项的顺序与布尔函数的真值表的顺序是一致的,即真值表中每一行的输入组合对应的最小项在最小项列表中的位置是一致的。
-
最小项表达式:布尔函数可以用一组最小项表示。最小项表达式是布尔函数的最简形式之一,它由最小项的逻辑乘积(AND)运算构成,每个最小项都表示了函数在相应输入组合下的输出。
-
仅有一个最小项的值为1。
-
全体最小项之和为1,任意两个最小项的乘积为0。
-
具有相邻性的两个最小项之和可以合并成一项并消去一对因子。
-
若两个最小项只有一个因子不同,则称这两个最小项具有相邻性。
5.1 用卡诺图将逻辑函数变成最小项的形式

5.2 用公式法将逻辑函数变成最小项的形式

5.3 将最小项的形式化成变量形式

5.4 卡诺图化简式子

6. 常用集成器件
译码器的概念:逻辑功能是将每个输入的二进制代码译成对应的输出高、低电平信号或另外一个代码。译码是反码的反操作。常见的译码器电路有二进制译码器,二-十进制译码器和显示译码器三类。
存储器:存储大量数据。其基本结构形式都由存储矩阵和读/写控制电路两部分组成。存储容量和存取速度是衡量存储器性能的两个重要指标。
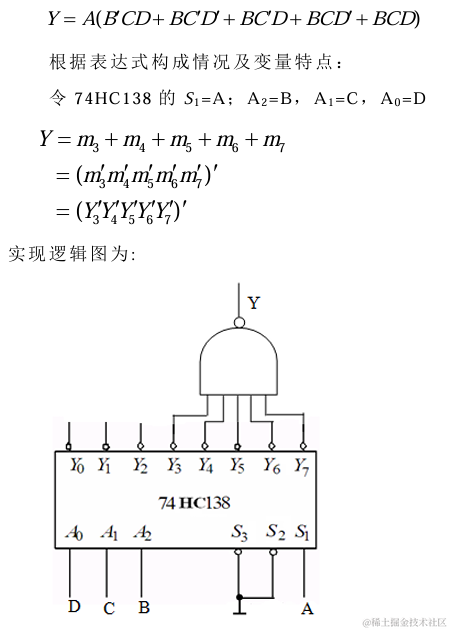
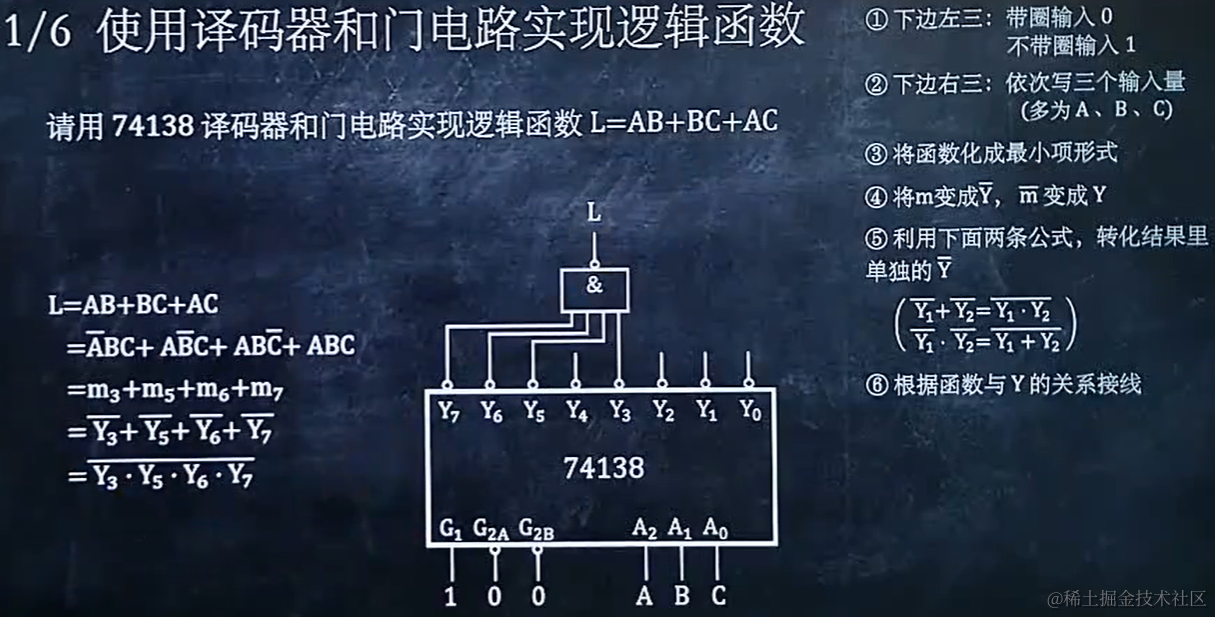
6.1 使用译码器和门电路实现逻辑函数

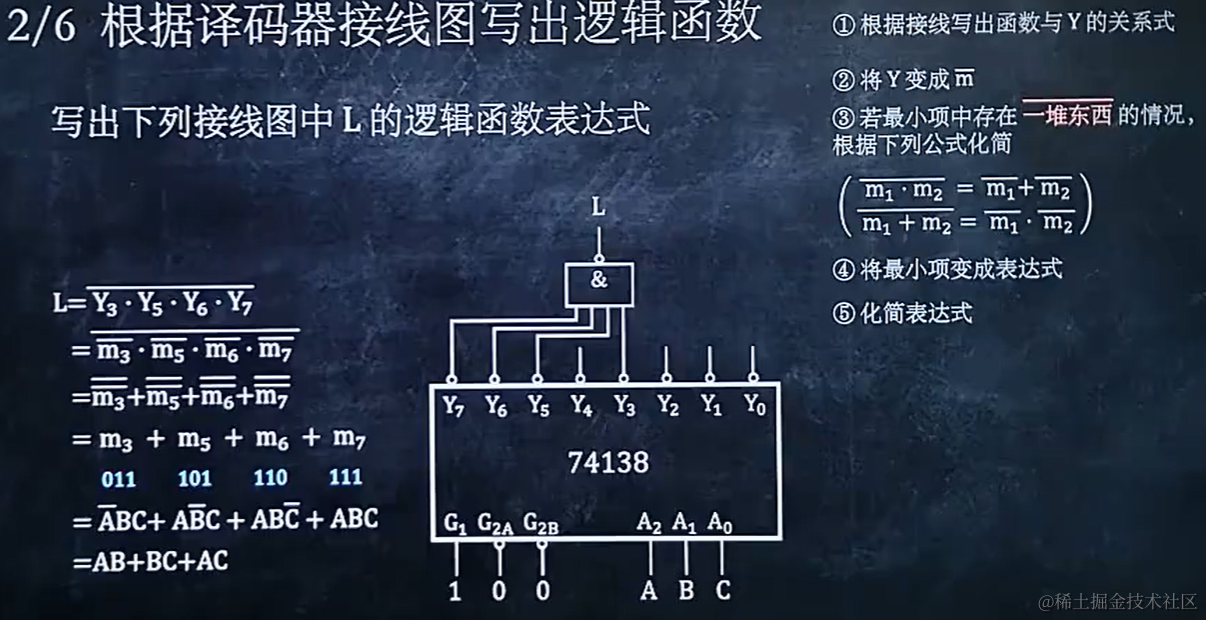
6.2 根据译码器接线图写出逻辑函数
6.3 使用八选一数据选择器实现三输入逻辑函数

6.4 使用八选一数据选择器实现多输入逻辑函数
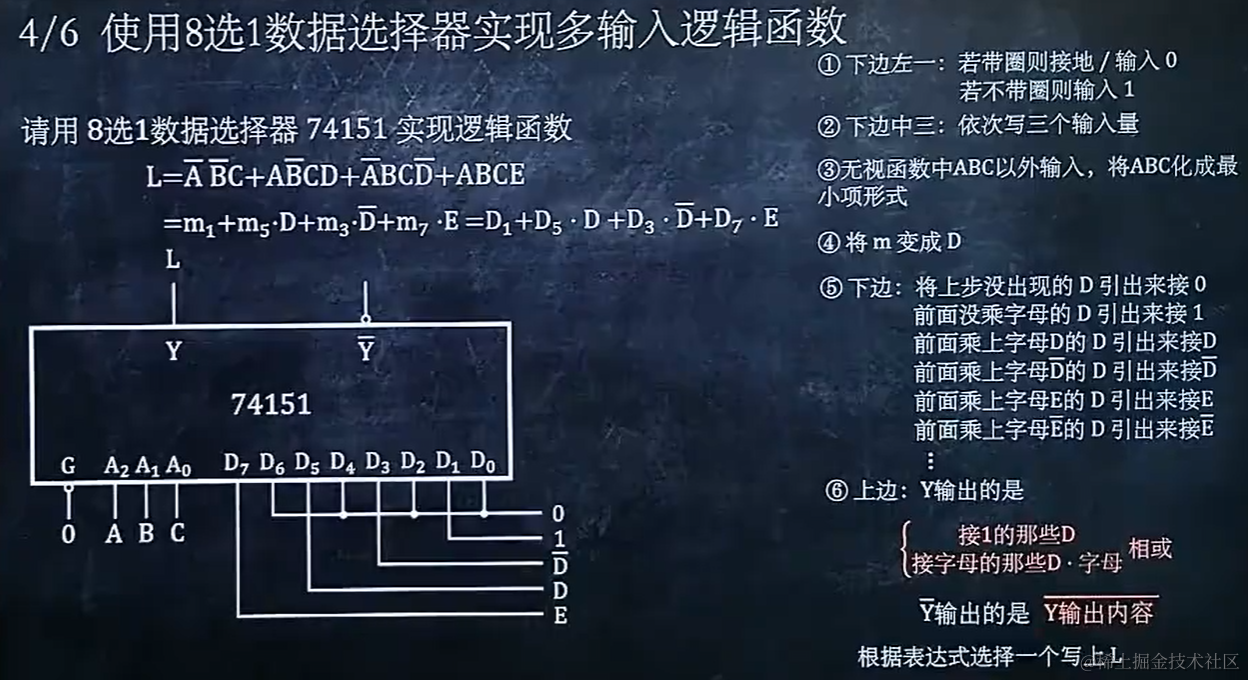
6.5 使用八选一数据选择器实现某格式的三输入逻辑函数
除了公式和上述方法没有区别。

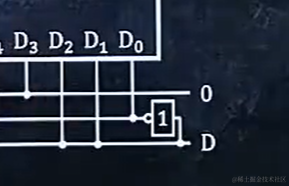
6.6 使用八选一数据选择器实现某格式的四输入逻辑函数

也可以写成这种形式:
7. 触发器
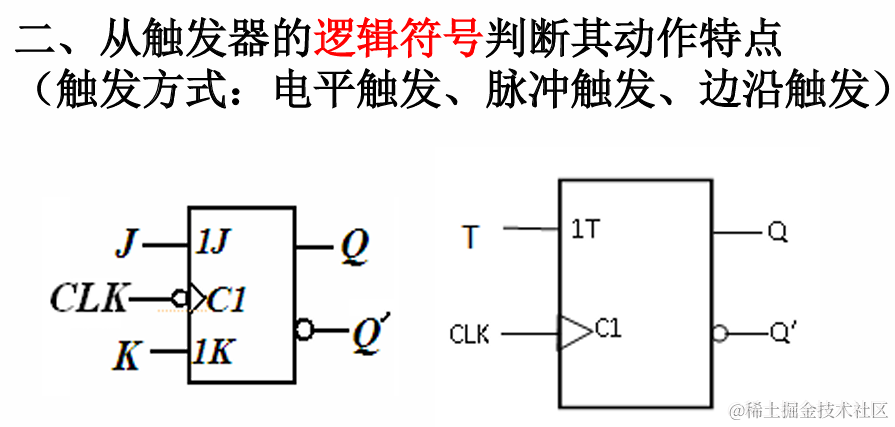
触发器是数字电路中用于存储和同步信号的重要元件。根据其逻辑功能和特性的不同,可以将触发器分为以下几类:
-
SR触发器(Reset-Set Trigger):SR触发器有两个输入端,分别是Reset(复位)和Set(设置)输入。它可以存储1比特的数据,并且可以被复位或设置为不同的值。
-
D触发器(Data Trigger):D触发器有一个输入端(Data)和一个时钟输入端(Clock)。当时钟信号的边沿触发时,D触发器将数据输入存储在其输出中。
-
JK触发器:JK触发器结合了RS触发器和T触发器的功能,可以实现更强大和灵活的功能。JK触发器具有两个输入端(J和K)和一个时钟输入端(Clock)。
-
T触发器(Toggle Trigger):T触发器有一个输入端(Toggle)和一个时钟输入端(Clock)。当时钟信号的边沿触发时,T触发器会将其输出翻转(0变为1,1变为0)。
JK触发器是一种具有多种逻辑功能的触发器。其逻辑功能可以通过输入端的不同组合来实现。下面是JK触发器的逻辑功能:
-
J = 0,K = 0(无操作):当J和K都为0时,JK触发器将保持其当前状态,不发生任何改变。
-
J = 0,K = 1(清零):当J为0,K为1时,JK触发器将强制将其输出置为0(复位)。
-
J = 1,K = 0(设定):当J为1,K为0时,JK触发器将强制将其输出置为1。
-
J = 1,K = 1(反转):当J和K都为1时,JK触发器将根据其先前状态,对输出进行翻转操作(1变为0,0变为1)。
注意,当J和K同时为1时,JK触发器的输出会根据时钟信号的边沿(上升沿或下降沿)进行翻转操作。这种操作也称为“触发”,因此该触发器得名为JK触发器。

7.1 给出 D 触发器及输入,要求画出波形图
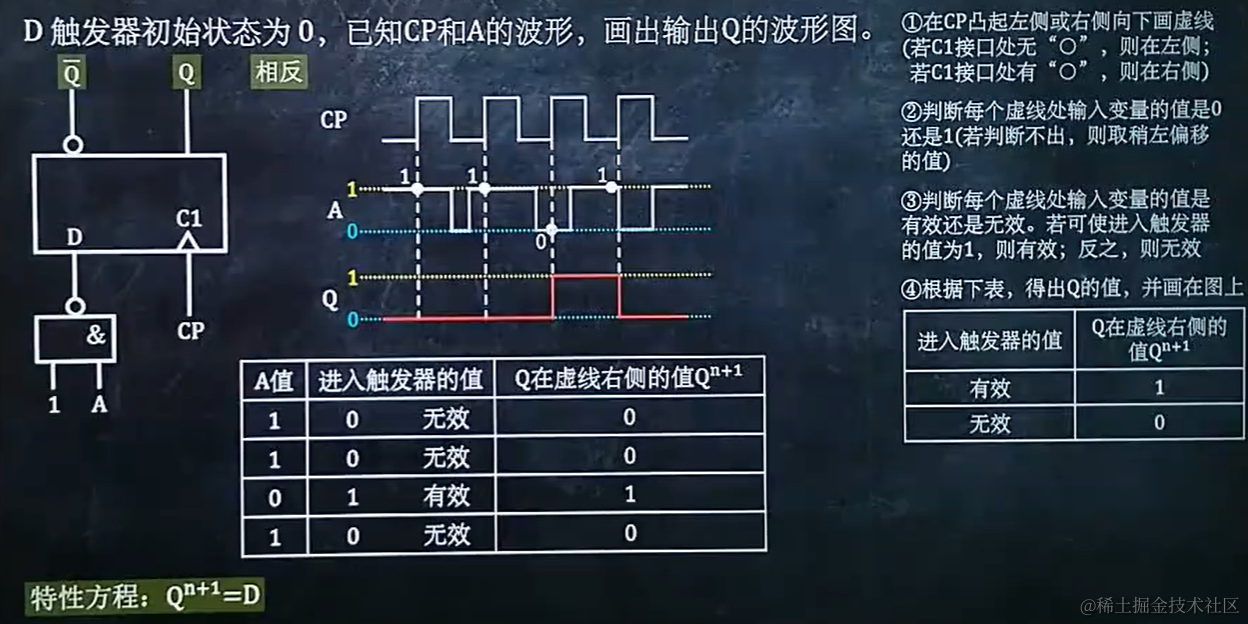
7.2 给出 JK 触发器及输入,要求画出波形图
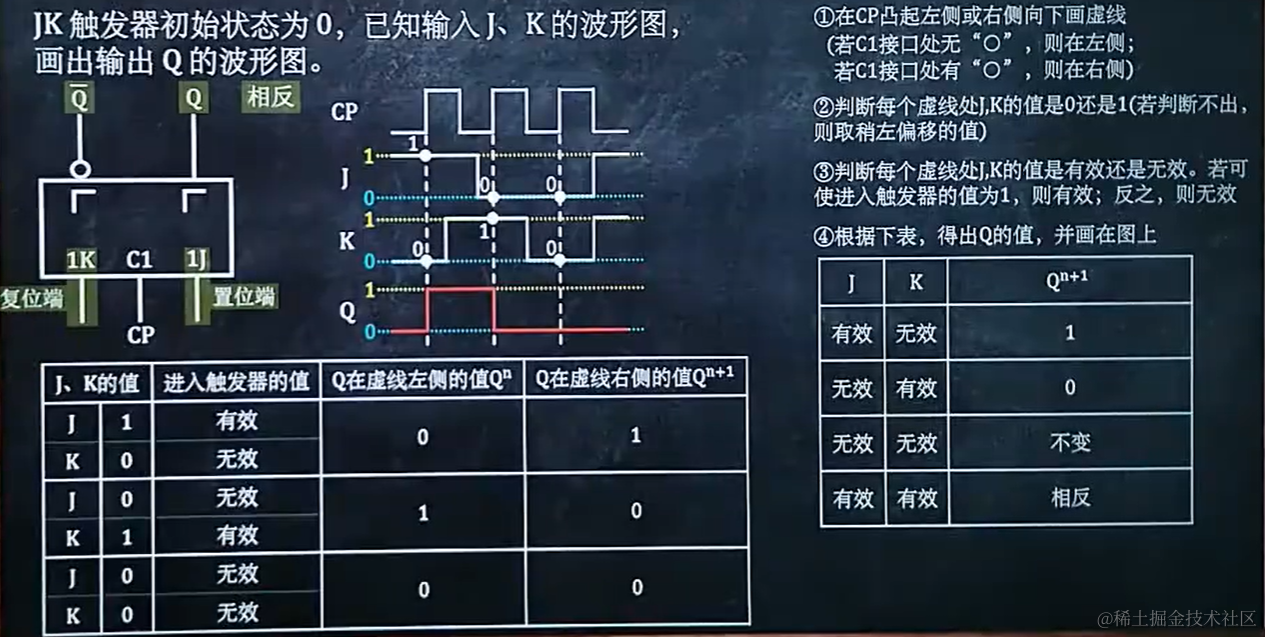
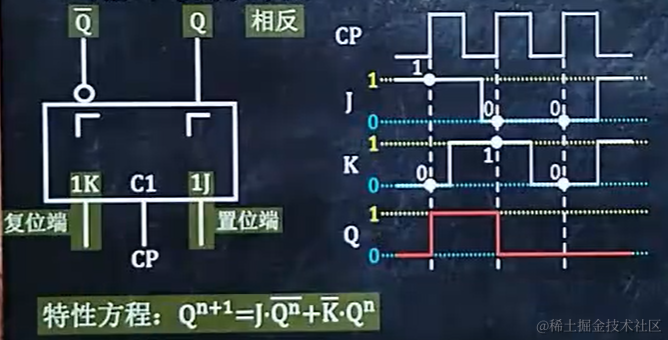
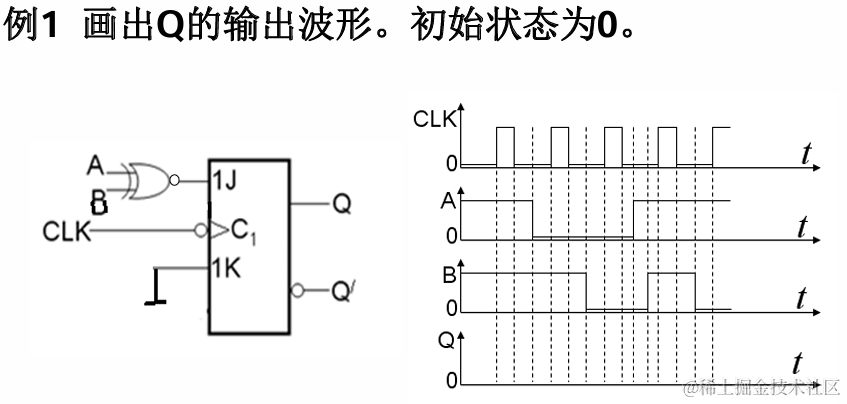
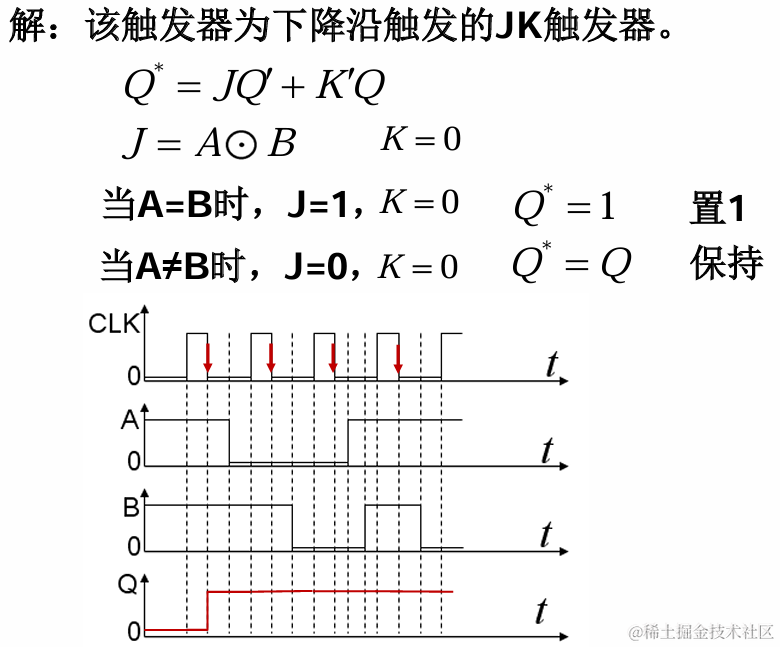
7.3 多个触发器相连

8. 计数器集成芯片
同步 + 1 = 异步
8.1 使用 74161 异步清零功能设计 N 进制计数器

8.2 使用 74161 异步清零功能设计 N 进制计数器后,画出状态图
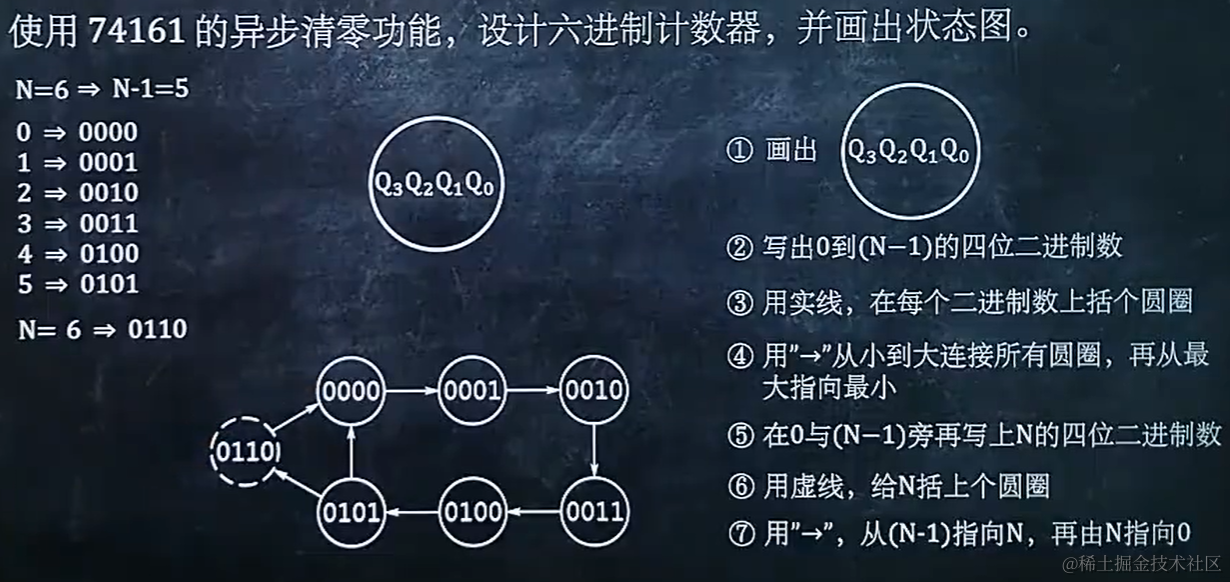
8.3 使用 74161 异步清零功能设计 N 进制计数器后,检查自启动
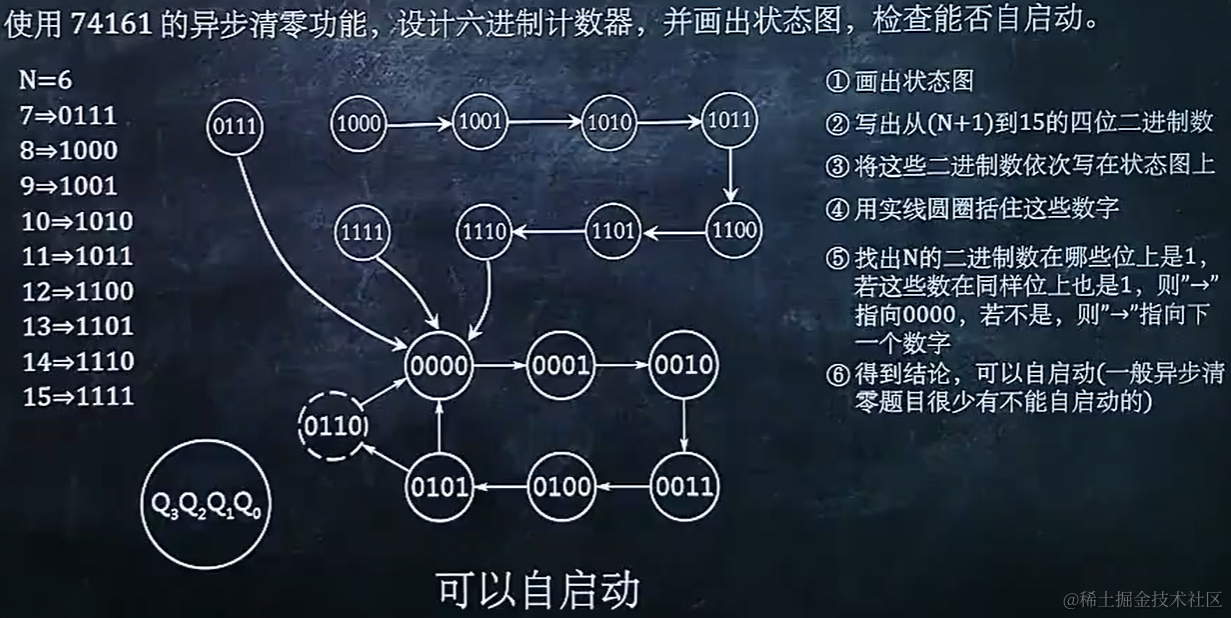
8.4 使用 74161 同步置数功能设计 N 进制计数器
异步清零,Q接RD。同步置数,RD接1。
同步置数,由大到小。小为D。从D代表的数值一直到Q代表的数值,为一个循环,即进制数。从中间向最大画圈。
异步清零,从D代表的数值一直到Q-1代表的数值,为一个循环,即进制数。从0向中间画圈。
画状态图不全画,判断自启动全画。
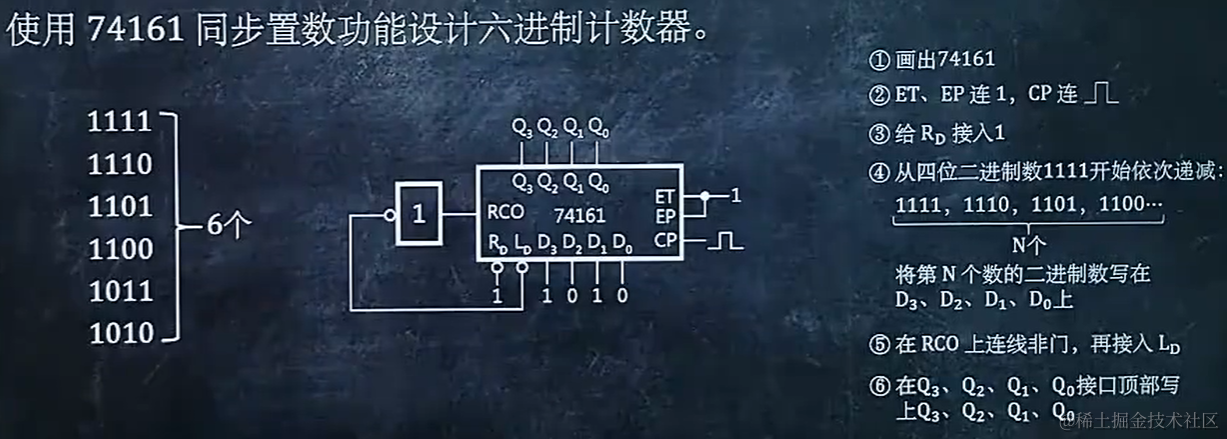
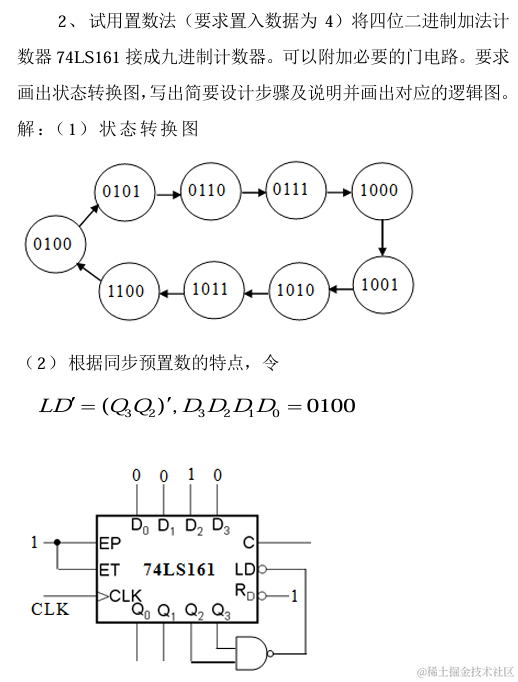
8.5 使用 74161 同步置数功能设计 N 进制计数器后,画出状态图
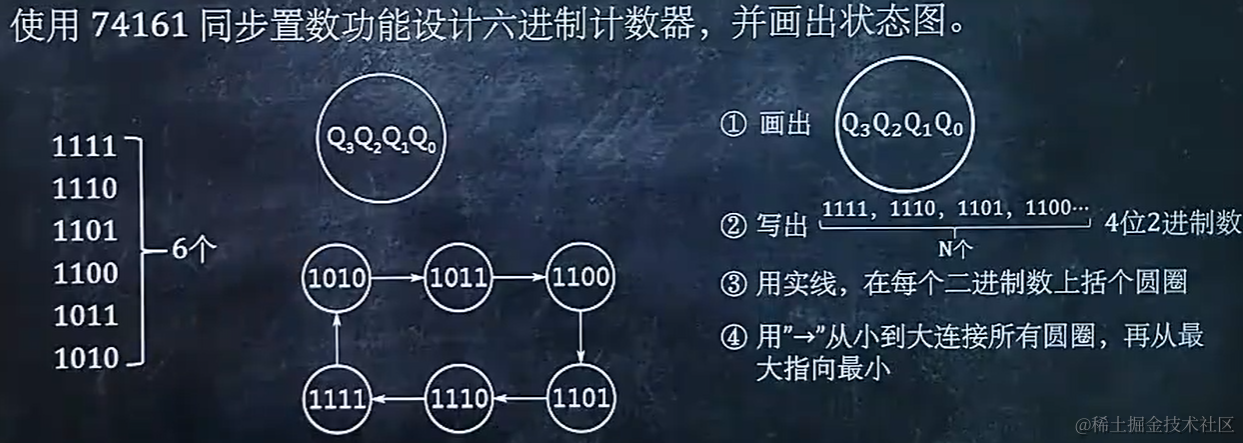
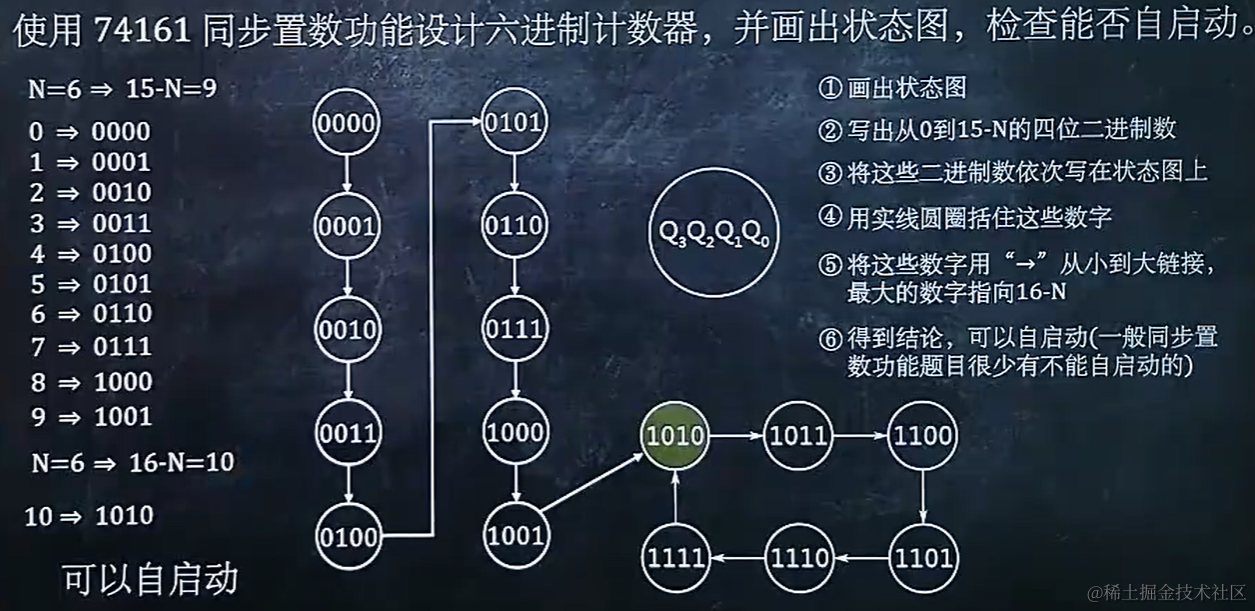
8.6 使用 74161 同步置数功能设计N进制计数器后,检查自启动使用
8.7 使用 74160 异步清零功能设计N进制计数器,并画状态图

8.8 使用 74160 同步置数功能设计 N 进制计数器
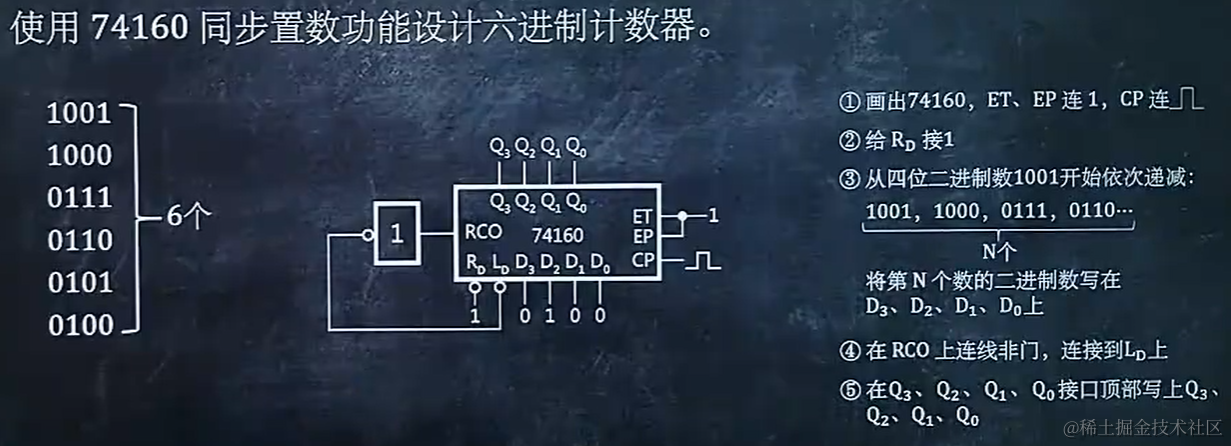
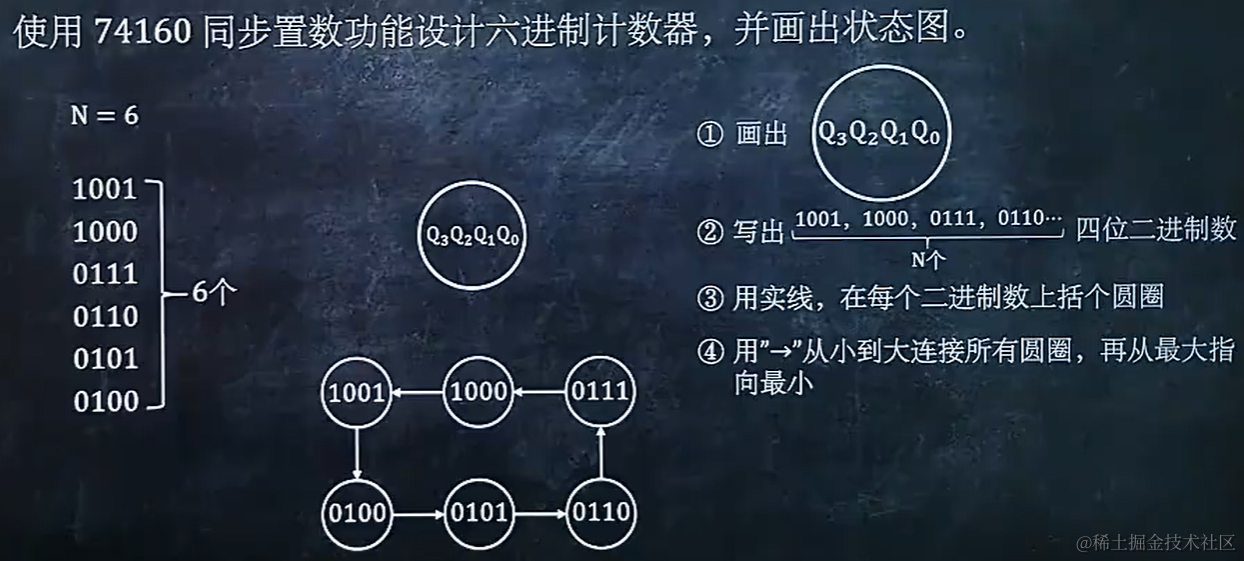
8.9 使用 74160 同步置数功能设计N进制计数器后,画出状态图
8.10 使用 74161 和 74151 设计某序列发生器
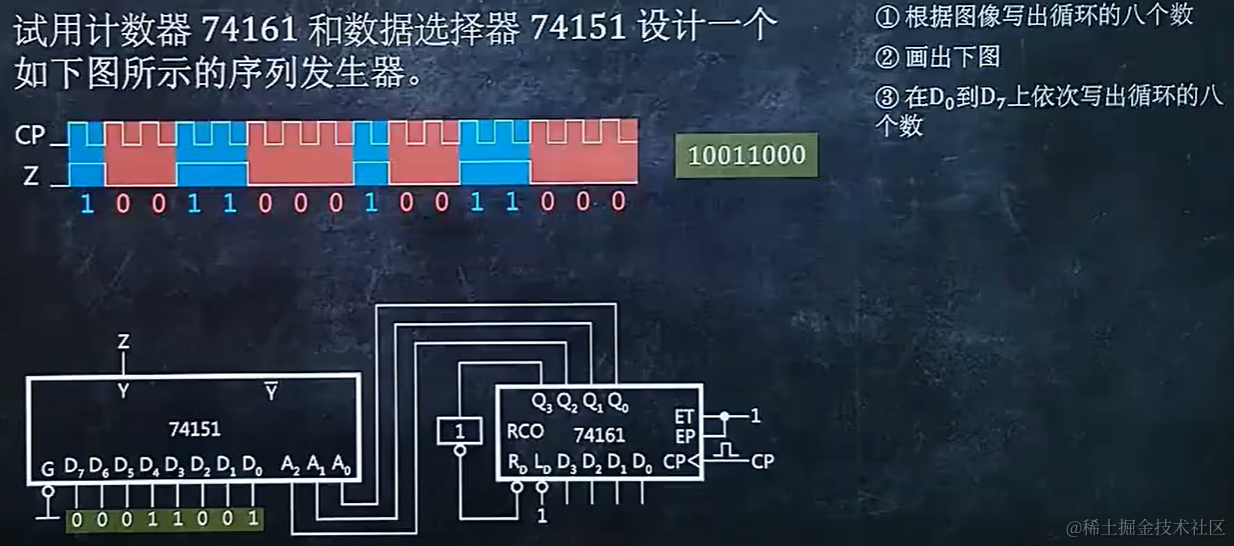
9. 分析时序逻辑电路
二进制加计数器是一种常见的数字逻辑电路,用于实现在二进制数上进行加法计数的功能。它可以按照预定的规则以二进制形式递增。
一个简单的二进制加计数器可以由一系列的触发器组成,如D触发器或JK触发器。这些触发器按照时钟信号的边沿进行触发,并且彼此连接以实现递归更新。
以下是一个4位二进制加计数器的简化步骤:
-
初始化:将所有触发器的初始状态设置为全零。
-
时钟信号触发:当时钟信号的边沿触发时,触发器的状态会相应更新。
-
进位传递:根据位的进位传递规则,在每个触发器之间连接一个逻辑电路来决定进位的传递。例如,对于4位计数器,进位传递通过逻辑门(如AND门)进行控制。
-
溢出处理:当计数器达到最大值时,即计数器的最高位触发器达到其最大状态时,可以生成一个溢出信号,用于指示溢出情况。
通过适当的电路设计和时钟控制,二进制加计数器可以实现从0开始逐次递增的计数。
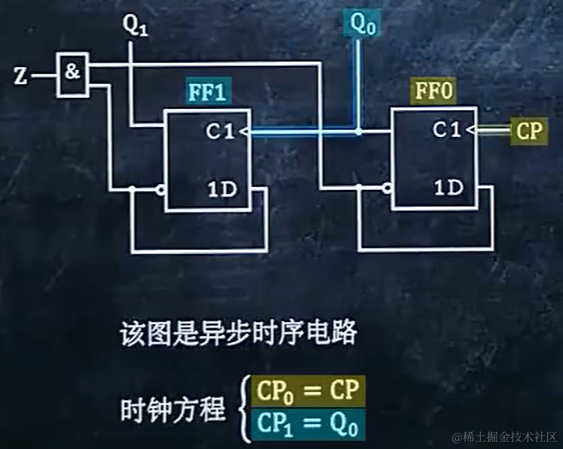
9.1 判断是同步时序电路还是异步时序电路,并写出时钟方程
如果两个C1接口连着一个口,则是同步;反之。
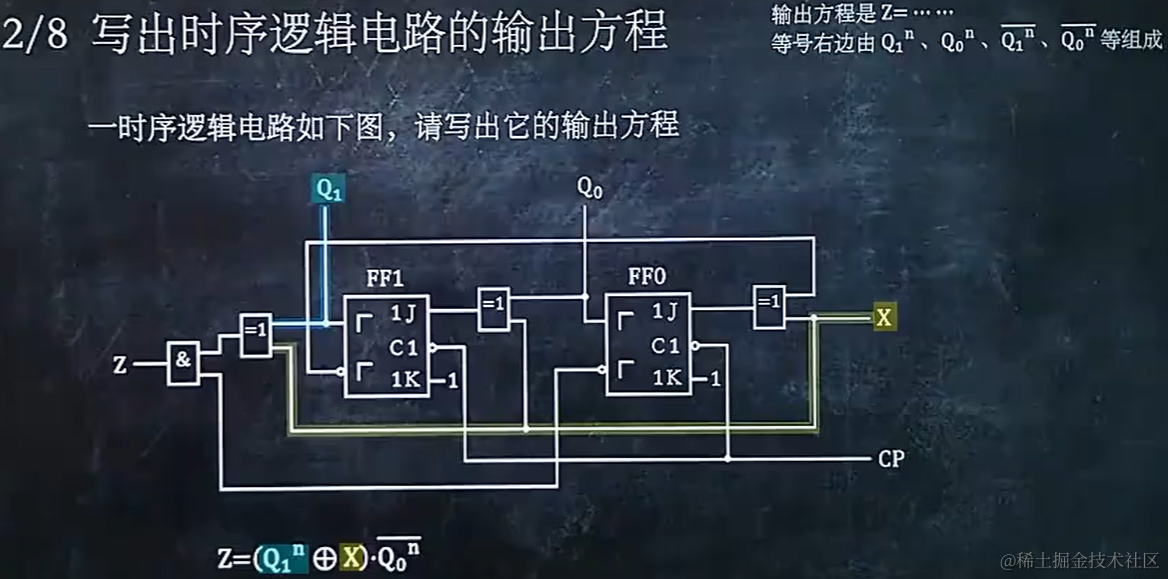
9.2 写出时序逻辑电路的输出方程
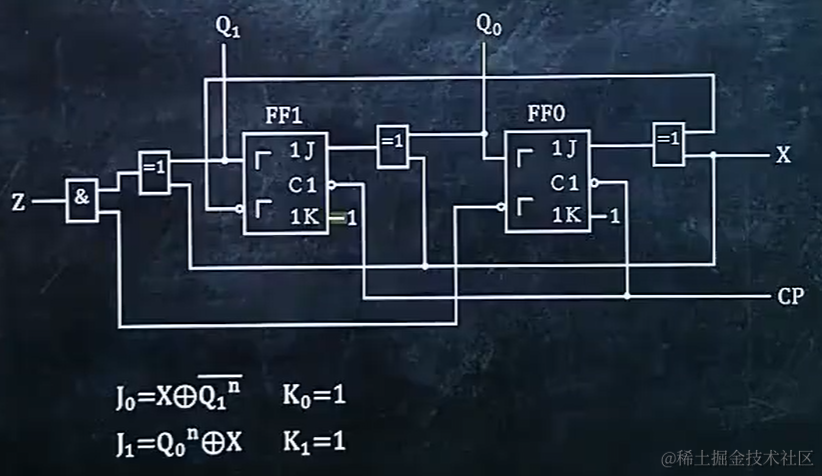
9.3 写出时序逻辑电路的驱动方程
9.4 写出时序逻辑电路的次态方程
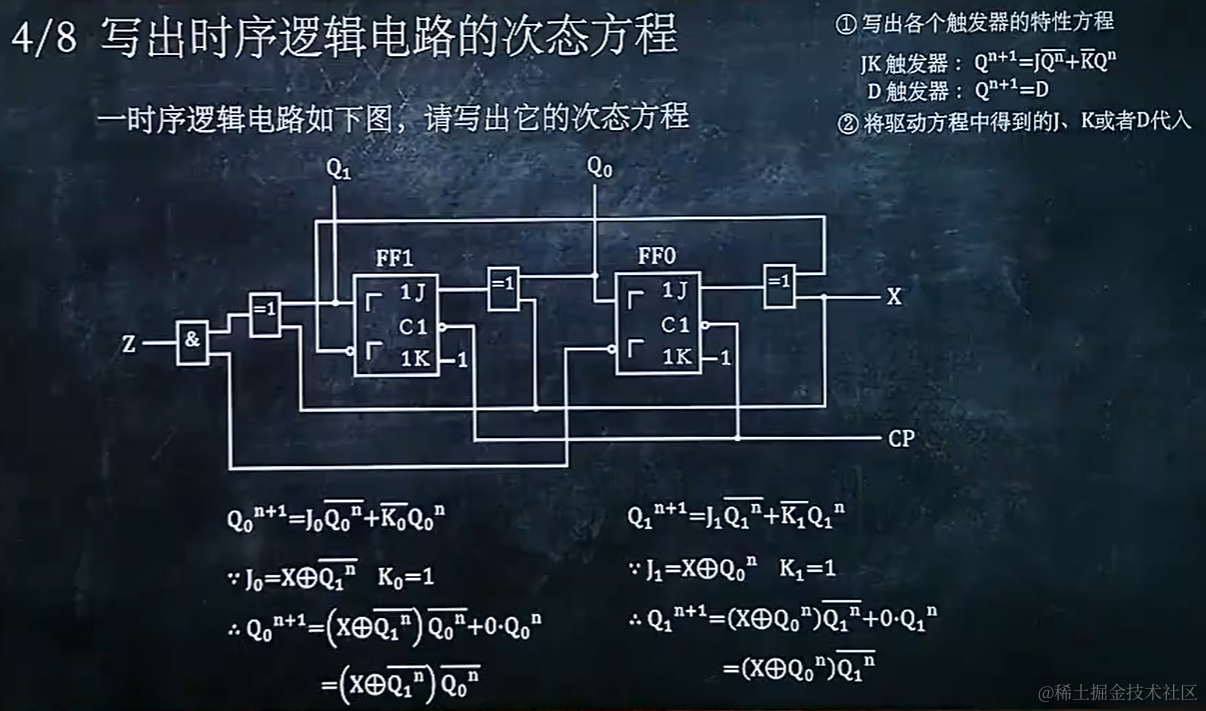
9.5 作时序逻辑电路的状态转换表

9.6 作时序逻辑电路的状态图
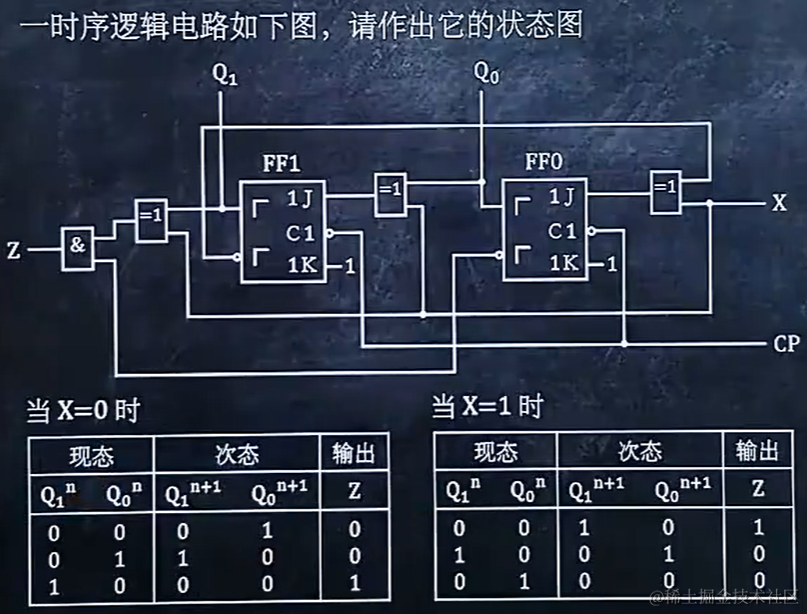
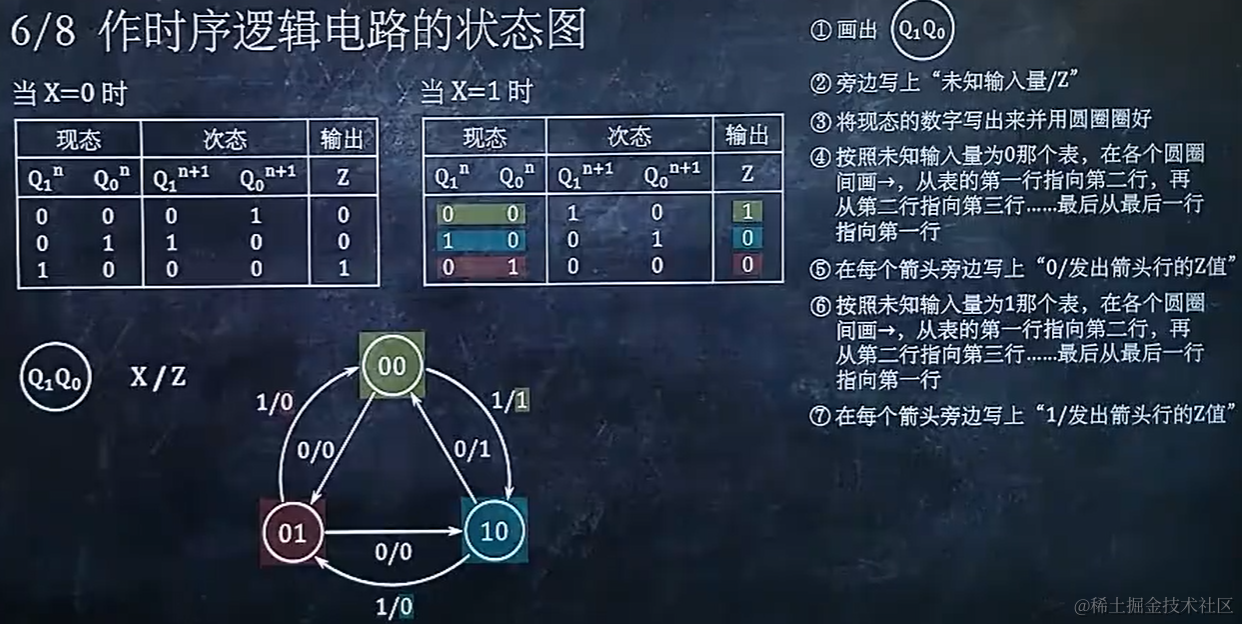
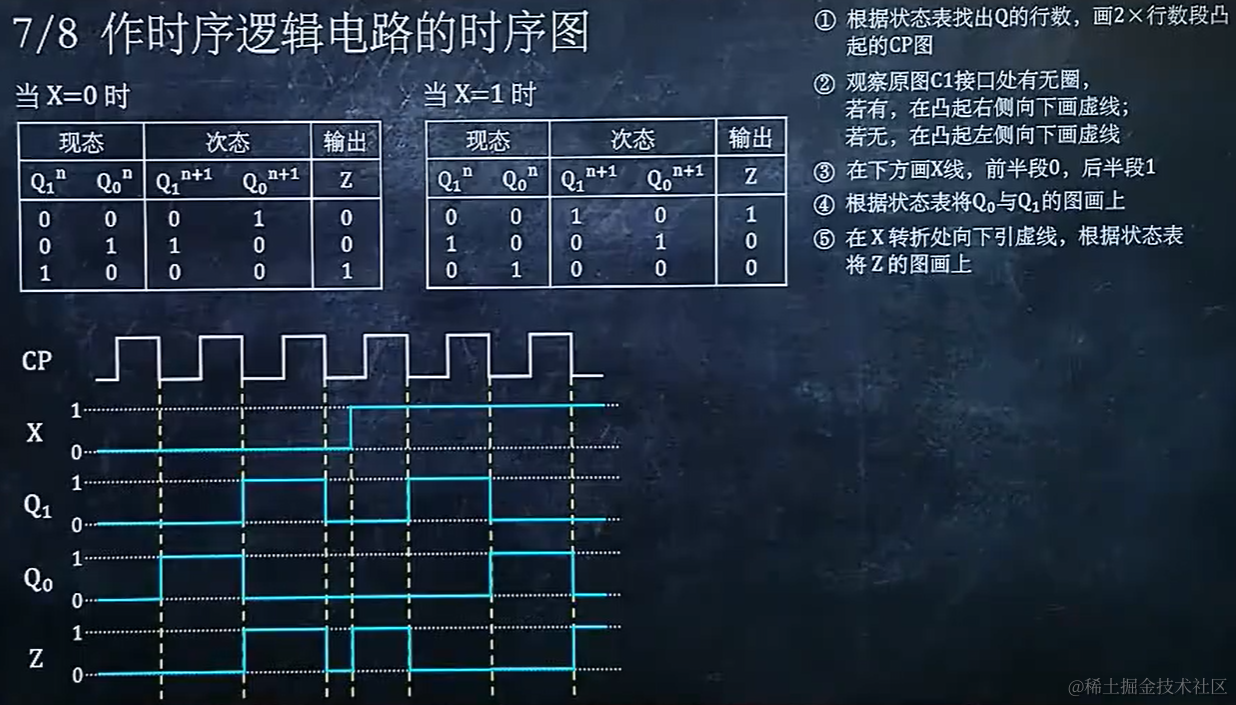
9.7 作时序逻辑电路的时序图
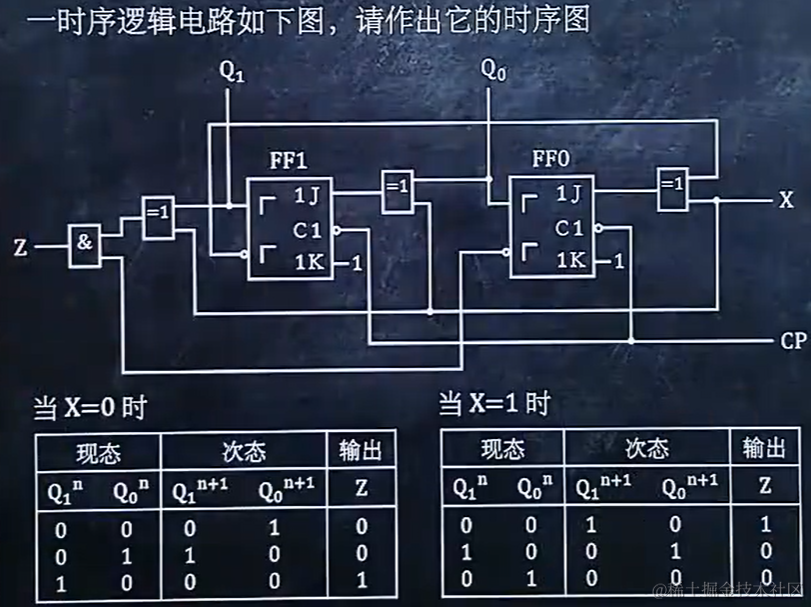
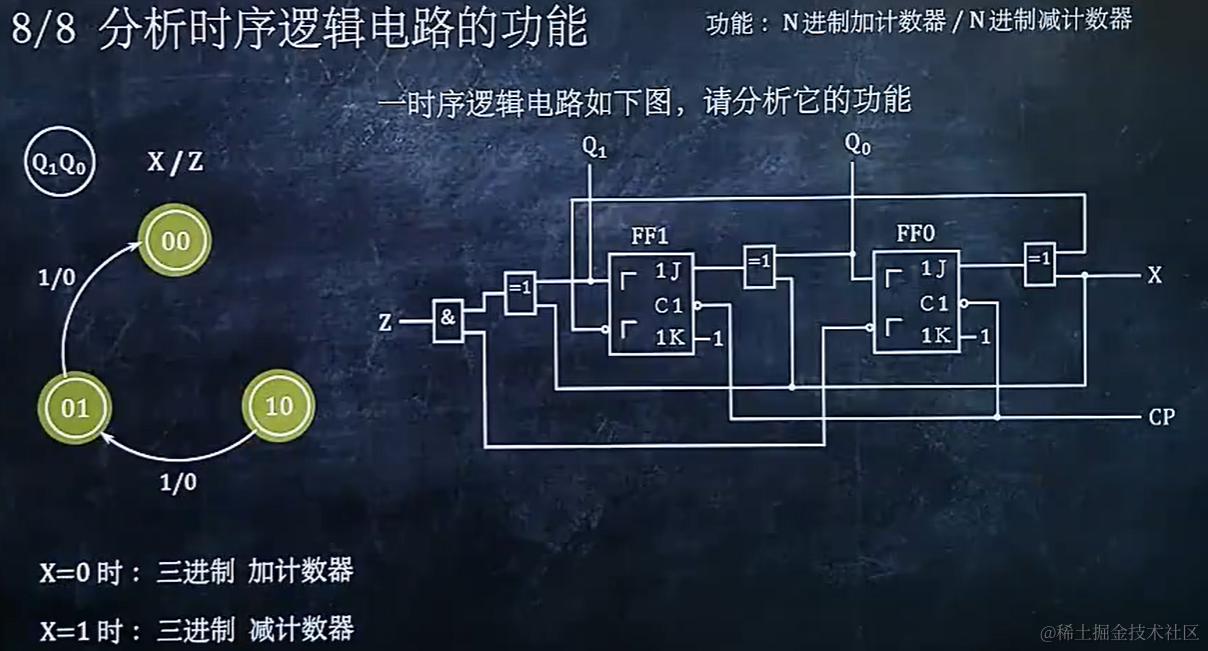
9.8 分析时序逻辑电路的功能
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!