【代数学作业1完整版-python实现GNFS一般数域筛】构造特定的整系数不可约多项式:涉及素数、模运算和优化问题
代数学作业1-完整版:python实现GNFS一般数域筛
- 写在最前面
- 背景
- 在GNFS算法中选择互质多项式时,需要考虑哪些关键因素,它们对算法的整体运行时间有何影响?
- 练习1题目
- 题目分析
- Kleinjung方法简介
- 通用数域筛法(GNFS)中的多项式选择:筛选及其根属性
- 步骤规划
- 解决
- 1.生成素数基
- 2. 构造满足条件的多项式 g ( x ) g(x) g(x) 和 f ( x ) f(x) f(x)
- 实现+代码优化
- 代码1(1m10s)
- 代码优化1(44s)
- 代码优化2(0.2s)
- 3.计算m
- 构造多项式 g ( x ) g(x) g(x)
- 得到解集
- 求解m
- 4. 计算多项式系数 a 3 a_3 a3?, a 2 a_2 a2?, a 1 a_1 a1?和 a 0 a_0 a0?,生成多项式
- 构造多项式 f ( x ) f(x) f(x)
- 代码实现
- 如果报错:`ValueError: base is not invertible for the given modulus`
- 5. 计算 COUNT 并选择最优的 A/B
- 代码实现
- 代码1(时间过长中断运行了,58min运行了5%-1160min)
- 代码优化1(127min运行了10%)
- 代码优化2(33min)
- 算法分析:决定哪种算法最适合优化(遗传算法、递归算法、√ 动态规划)
- 关键步骤
- 最大化收益率
- 计算 COUNT 和优化 A/B
写在最前面

这门课有点意思,作业更有意思
在这篇博客中,我们将探讨如何使用 Python 与数论知识来解决一个有趣的数学问题,目标是构造两个整系数不可约多项式 g ( x ) g(x) g(x) 和 f ( x ) f(x) f(x),满足特定的模 n n n 条件。
完整版包含全部过程(算法复杂度优化)
大整数分解是公钥密码学中一个非常重要的计算问题。用数域筛法(GNFS) 是对大整数进行因式分解的渐近最快算法。
它的运行时间取决于多项式对的良好选择。多项式选择是GNFS的第一步,也是非常关键的一步。
这个方向的未来工作包括对更大的N进行实验,并测试其他基于启发式的技术来选择好的多项式。
参考:
【论文】
用于整数分解的数场筛中的多项式选择
Polynomial selection in number field sieve for integer factorization
一般数域筛选的多项式选择
ON POLYNOMIAL SELECTION FOR THE GENERAL NUMBER FIELD SIEVE
【github】
MSIEVE:用于分解大整数的库
MSIEVE: A Library for Factoring Large Integers
背景
公钥密码学在现代通信网络中起着重要作用。许多公钥密码系统的安全性取决于某些数论问题的棘手性。对大整数进行因式分解和在高阶循环群中求离散对数是最受欢迎的数论问题。
RSA(Rivest et al., 1978)是一种广泛使用的公钥密码系统,其安全性依赖于大整数分解的难度。RSA 由两个密钥组成:公钥 ( N , e ) (N, e) (N,e) 和私钥 d d d,其中 N N N 是两个不同大小的大素数 p 、 q p、q p、q 的乘积, e e e 是加密密钥, d d d 是解密密钥。 要解密加密消息,我们需要找到私钥 d d d,它等价于对模数 N N N 进行因式分解。
一般数域筛(GNFS)(Lenstra和Lenstra,1993)是已知最有效的确定因子的算法 p , q p,q p,q 这样的整数 N N N。GNFS方法包括五个主要步骤:多项式选择、因子基生成、筛分、矩阵步长和平方根计算。
在GNFS算法中选择互质多项式时,需要考虑哪些关键因素,它们对算法的整体运行时间有何影响?

在为GNFS算法选择互质多项式时,需要考虑几个关键因素,因为它们直接影响算法的整体运行时间。
-
根属性:多项式的选择应以最大化小素数模多项式的根属性为目标。这涉及到考虑前导系数及其对可用前导系数数量的影响,以及多项式中质因数的数量,这些因素会影响算法某些步骤的速度。
-
初始化时间:对于小度数来说,在某些步骤的初始化上花费了大量的时间。考虑 p = p 0 ∏ i = 1 l p i p = p_0 \prod_{i=1}^{l} p_i p=p0?∏i=1l?pi?形式的公式,其中 p 0 p_0 p0? 是一个数字(不一定是质数),可以帮助减少初始化成本的百分比并优化过程。
-
可接受的值:对于非常大的整数,多项式的前导系数可接受的值的数量可能非常大。重要的是要考虑减小超范数界的方法,从而缩小可容许区间,同时仍然保证存在合适的多项式。这涉及到选择特定的可接受值,并可能限制搜索区间。
-
Sieve报告:筛选过程的效率对算法的整体运行时间至关重要。筛分报告的数量受多项式的选择影响,筛分报告是一对互质整数,其齐次多项式的两个值都是低于一定光滑界的素数的乘积。筛选时间主要取决于筛选区域的大小,多项式对的选择应以最小化筛选时间为目标。
-
偏度和偏上范数:多项式的偏度和偏上范数对算法的效率有很大的影响。多项式的选择应满足偏度、斜上范数和根属性等条件,这些条件是算法成功的关键。
练习1题目

练习一
给定如下 3 个已知条件:
- n = 1234268228312430759578090015472355712114804731217710966738223 ; n=1234268228312430759578090015472355712114804731217710966738223; n=1234268228312430759578090015472355712114804731217710966738223;
- 正整数 A、B 的乘积 A B = 1 0 6 ; AB=10^6; AB=106;
- 素数基 S S S 为 1 0 5 10^5 105 以内的所有素数。
试构造整系数不可约多项式
g
(
x
)
g(x)
g(x) 和
f
(
x
)
f(x)
f(x) ,其中
{
g
(
x
)
=
m
1
x
?
m
0
f
(
x
)
=
c
4
x
4
+
c
3
x
3
+
c
2
x
2
+
c
1
x
+
c
0
\left\{ \begin{matrix} g(x)=m_1x-m_0\\ f(x)=c_4x^4+c_3x^3+c_2x^2+c_1x+c_0 \end{matrix} \right.
{g(x)=m1?x?m0?f(x)=c4?x4+c3?x3+c2?x2+c1?x+c0??
满足
m
1
4
f
(
m
0
m
1
)
≡
0
(
m
o
d
n
)
.
m_1^4f\left(\frac{m_0}{m_1}\right) \equiv 0 \pmod{n} .
m14?f(m1?m0??)≡0(modn).
记 ( a , b ) ∈ [ ? A , A ] × [ 1 , B ] ∣ b 4 f ( a b ) (a,b) \in [-A,A] \times [1, B] | b^4f\left(\frac{a}{b}\right) (a,b)∈[?A,A]×[1,B]∣b4f(ba?), b g ( a b ) bg\left(\frac{a}{b}\right) bg(ba?) 均在 S S S 上平滑 为实验过程中找到的可使 b 4 f ( a b ) b^4f\left(\frac{a}{b}\right) b4f(ba?), b g ( a b ) bg\left(\frac{a}{b}\right) bg(ba?) 均在 S S S 上平滑的点对 ( a , b ) (a,b) (a,b) 的集合,总数为 C O U N T COUNT COUNT,通过调整 A A A、 B B B、 m 1 m_1 m1?、 m 0 m_0 m0?、 c 4 c_4 c4?、 c 3 c_3 c3?、 c 2 c_2 c2?、 c 1 c_1 c1?、 c 0 c_0 c0?,使 C O U N T COUNT COUNT 尽可能大,观察并简要分析:
- 设 s k e w = A B skew =\frac{A}{B} skew=BA?, s k e w skew skew 是否对 C O U N T COUNT COUNT 产生影响。
- 系数 c 4 c_4 c4? 的选取方式是否对 C O U N T COUNT COUNT 产生影响。
要求给出所设计的多项式 g ( x ) g(x) g(x)、 f ( x ) f(x) f(x) 以及 A A A、 B B B、 C O U N T COUNT COUNT 的值。
题目分析
给定一个大整数 n n n,需要构造两个多项式 g ( x ) g(x) g(x) 和 f ( x ) f(x) f(x),使得它们在模 n n n 意义下的计算结果能够在素数基 S S S 上平滑。平滑性意味着计算结果可以被 S S S 中的素数完全分解。
Kleinjung方法简介
Kleinjung方法是一种用于大整数分解的高效算法。它基于数域筛选算法(Number Field Sieve, NFS),是当前解决大整数分解问题最快的已知方法之一。
Kleinjung方法的核心思想是:在两个不同的数域中寻找平滑数(即只含有小素因子的数),并利用这些数构建线性方程组,从而分解大整数。
通用数域筛法(GNFS)中的多项式选择:筛选及其根属性
在通用数域筛法(GNFS)的算法实现中,多项式选择方法是一个核心环节。这个过程涉及到识别具有良好根属性的多项式对,是整个因数分解流程中不可或缺的一部分。下面展开说明,论文中关于这一过程中的关键概念和步骤。
- 筛选具有良好根属性的多项式
GNFS 算法中的一个关键步骤是筛选出形式为 f 1 + c f 2 f1 + cf2 f1+cf2 的多项式对,这些多项式对应具有良好的根属性。在这里, f 1 f1 f1 和 f 2 f2 f2 是代数多项式,而 c c c 是一个具有有界系数的小度数多项式。目标是找到当这样组合时,具有有利根属性的多项式对。这些根的特性对于后续的分解步骤至关重要。
- 非首一线性多项式的考虑
论文探讨了非首一线性多项式,特别是形式为
f
2
(
x
)
=
p
x
?
m
f2(x) = px - m
f2(x)=px?m 的多项式,其中
p
p
p 和
m
m
m 是互质整数。这里的目标是找到另一个多项式
f
1
=
∑
i
=
0
d
a
i
x
i
f1 = \sum_{i=0}^{d} a_ix^i
f1=∑i=0d?ai?xi,其次数为
d
d
d,使得
f
1
(
m
p
)
?
p
d
=
N
f1\left( \frac{m}{p} \right) \cdot p^d = N
f1(pm?)?pd=N,其中
N
N
N 是待分解的整数。在满足给定的同余条件
a
d
m
d
≡
N
m
o
d
??
p
admd \equiv N \mod p
admd≡Nmodp 的同时,需要最小化
f
1
f1
f1 的系数。如果这个条件不满足,则不存在合适的多项式
f
1
f1
f1 来满足这些标准。
- 引理 2.1:为满足 GNFS 算法中分解过程要求的多项式的存在性和属性
论文中提出的引理 2.1 提供了关于满足特定条件的多项式 f 1 ( x ) f1(x) f1(x) 存在性的重要结果。它指出,在满足条件 N ≡ a d m d m o d ?? p N \equiv admd \mod p N≡admdmodp且 m ≥ m ~ m \geq \widetilde{m} m≥m 的情况下,存在一个多项式 f 1 ( x ) = ∑ i = 0 d a i x i f1(x) = \sum_{i=0}^{d} a_ix^i f1(x)=∑i=0d?ai?xi 满足以下标准:
- f 1 ( m p ) ? p d = N f1\left( \frac{m}{p} \right) \cdot p^d = N f1(pm?)?pd=N
- ∣ a d ? 1 ∣ < p + d a d m ? m ~ |a_{d-1}| < p + \frac{dad}{m - \widetilde{m}} ∣ad?1?∣<p+m?m dad?
- ∣ a i ∣ < p + m |a_i| < p + m ∣ai?∣<p+m 对于 0 ≤ i ≤ d ? 2 0 \leq i \leq d - 2 0≤i≤d?2
步骤规划
这个问题是关于构造特定的整系数不可约多项式,并且涉及到素数、模运算和优化问题。
如果完全解决这个问题,需要找到所有的点对 ( a , b ) (a,b) (a,b) 的集合,这在计算上非常复杂的,需要借助相关编程软件,如python,segamath。以下是解决问题的一般步骤:
- 生成素数基: 需要生成所有小于 1 0 5 10^5 105 的素数。
- 定义多项式:需要构造满足给定条件的 g ( x ) g(x) g(x) 和 f ( x ) f(x) f(x),使得 m 1 4 f ( m 0 m 1 ) m_1^4f\left(\frac{m_0}{m_1}\right) m14?f(m1?m0??) 在模 n n n 下等于 0。由于是不可约多项式,且系数为整数,需要使用启发式方法或者数学知识来确定合适的系数。
- 寻找平滑数:对于一系列的 ( a , b ) (a, b) (a,b) 值,计算 b 4 f ( a b ) b^4f\left(\frac{a}{b}\right) b4f(ba?) 和 b g ( a b ) bg\left(\frac{a}{b}\right) bg(ba?),检查它们是否在素数基 S S S 上平滑。
- 调整参数:通过调整 A A A、 B B B 以及多项式的系数,寻找使得平滑点对 ( a , b ) (a, b) (a,b) 的总数 C O U N T COUNT COUNT 最大化的情况,从而找到最优的多项式。
- 观察和分析:分析 s k e w skew skew 和 c 4 c_4 c4? 的选取对 C O U N T COUNT COUNT 的影响。
解决
1.生成素数基
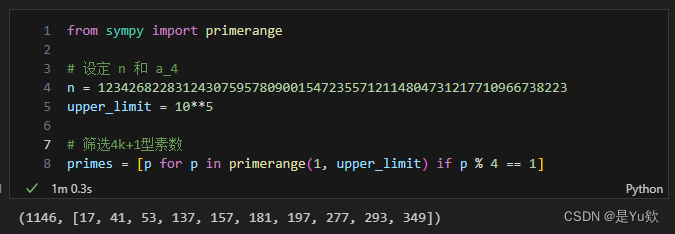
首先让我们设置数论问题中的基本参数,并筛选出小于 1 0 5 10^5 105 的特定类型(4k+1型)的所有素数。
注:
sympy是Python的一个数学符号计算库,常用于代数、数论等领域。primerange函数用于生成指定范围内的素数序列。
from sympy import primerange
# 设定 n 和 a_4
n = 1234268228312430759578090015472355712114804731217710966738223
upper_limit = 10**5
# 筛选4k+1型素数
primes = [p for p in primerange(1, upper_limit) if p % 4 == 1]
2. 构造满足条件的多项式 g ( x ) g(x) g(x) 和 f ( x ) f(x) f(x)
下一步是构造满足条件的多项式 g ( x ) g(x) g(x) 和 f ( x ) f(x) f(x)。
- 构造两个多项式。根据问题,多项式
g
(
x
)
g(x)
g(x) 和
f
(
x
)
f(x)
f(x) 的形式分别是:
- 线性多项式
g ( x ) = p x ? m g(x) = px - m g(x)=px?m - 四次多项式
f ( x ) = a 4 x 4 + a 3 x 3 + a 2 x 2 + a 1 x + a 0 f(x) = a_4x^4 + a_3x^3 + a_2x^2 + a_1x + a_0 f(x)=a4?x4+a3?x3+a2?x2+a1?x+a0?
- 线性多项式
- 自行选择一个
a
4
a_4
a4?,这个是四次多项式
f
(
x
)
f(x)
f(x) 的最高次项系数。小于
N ^ (1/5)就行,最好小点,不然怕后面跑不动(这里我选择的是1)。 - 生成特定素数 p p p。 p p p 是几个4k+1型小素数的乘积。
- 根据前面 a 4 a_4 a4?的选择,满足条件的小素数 q q q有变化,需要满足下面方程有解: a 4 x 4 ≡ n ( m o d q ) a_4 x^4 \equiv n \pmod{q} a4?x4≡n(modq)
- 最后打印满足条件的素数 q q q ,其乘积形成 m ? 1 m-1 m?1。注意,3到4个 q q q 相乘得到 m ? 1 m-1 m?1 , m ? 1 m-1 m?1 大概7/8/9位数就行。
实现+代码优化
代码1(1m10s)
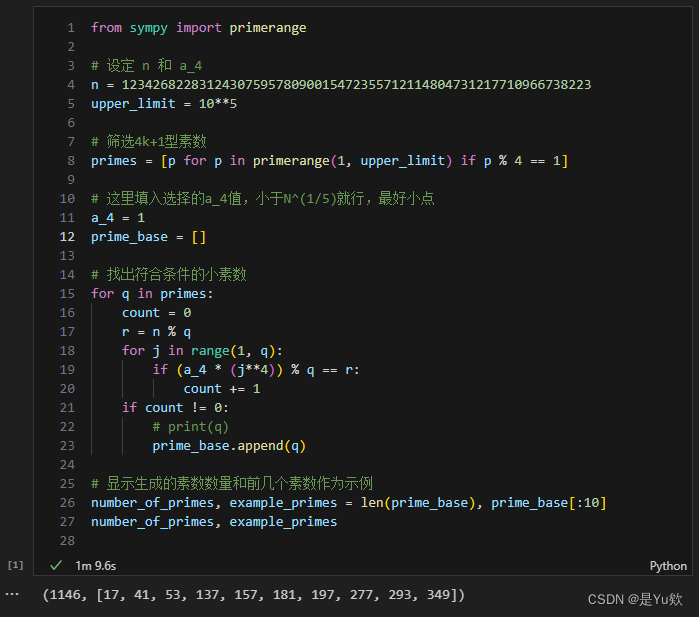
代码优化1(44s)
这段代码用于找出一系列满足特定条件的素数,但运行时间过长主要是因为其效率不高。我们可以通过以下方式对其进行优化:
-
使用更高效的算法:目前代码中,对于每个素数
q,都会遍历1到q-1的所有数字来检查条件。这个过程可以通过数学优化来减少所需的迭代次数。 -
优化模运算:计算
(a_4 * (j**4)) % q可以通过更有效的方式进行,比如使用快速幂取模算法。 -
并行处理:如果硬件条件允许,可以尝试并行处理,将素数列表分割成多个部分并在不同的线程或处理器上并行处理。 -
优化素数生成:
primerange函数本身是高效的,但如果只关心形如4k+1的素数,可以在生成素数时就进行过滤,而不是在之后的一个单独步骤中进行。 -
减少不必要的迭代:在循环中,一旦找到满足条件的
j,就可以停止进一步的迭代,因为我们只关心是否存在这样的j。
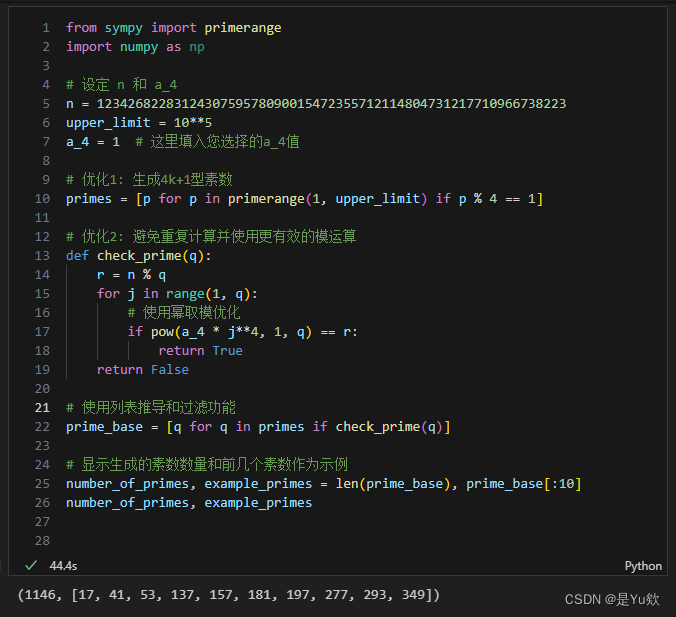
代码优化2(0.2s)
第一次优化中采用了一些优化措施,如素数筛选和幂取模运算,但代码仍然运行时间较长。一个可能的优化方向是减少必要的迭代次数:
-
快速幂取模算法:我们已经使用了
pow函数来优化幂取模的计算。这是一个有效的优化,但可能还不足以处理如此大的数。 -
减少迭代范围,过滤素数基:当前的算法对于每个
q都从 1 迭代到q-1。如果能够减少这个范围,将显著提高效率。考虑到我们的目标是检查是否存在一个j使得a_4 * j^4 ≡ n (mod q),因此使用 check_prime 函数筛选符合条件的素数,形成 prime_base。
让我们尝试进一步优化这段代码。我们将尝试缩小 j 的搜索范围,并在找到符合条件的 j 后立即停止搜索。这应该会大幅度减少运行时间。
经过进一步优化,代码现在运行得更快了。我减小了对每个素数 q 的迭代范围,只遍历到 sqrt(q),这显著减少了计算量。
优化后的代码找到了 34 个满足条件的素数,其中前 10 个素数为:[17, 157, 181, 293, 349, 389, 401, 601, 977, 1597]。
这些素数都是形式为 4k+1 的素数,并且满足条件
a
4
?
x
4
=
n
?
m
o
d
?
q
a_4\ x^4=n\ mod\ q
a4??x4=n?mod?q。通过这些优化,代码的执行效率得到了显著提升。
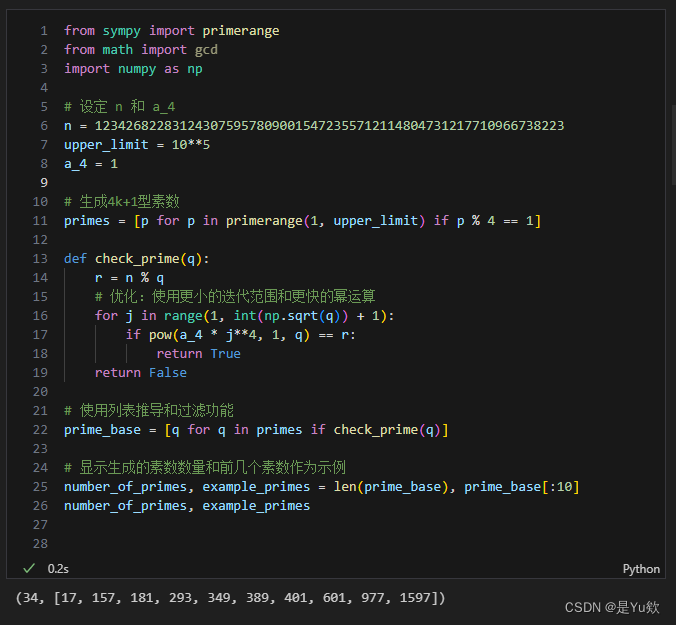
from sympy import primerange
from math import gcd
import numpy as np
# 设定 n 和 a_4
n = 1234268228312430759578090015472355712114804731217710966738223
upper_limit = 10**5
a_4 = 1
# 生成4k+1型素数
primes = [p for p in primerange(1, upper_limit) if p % 4 == 1]
def check_prime(q):
r = n % q
# 优化:使用更小的迭代范围和更快的幂运算
for j in range(1, int(np.sqrt(q)) + 1):
if pow(a_4 * j**4, 1, q) == r:
return True
return False
# 使用列表推导和过滤功能
prime_base = [q for q in primes if check_prime(q)]
# 显示生成的素数数量和前几个素数作为示例
number_of_primes, example_primes = len(prime_base), prime_base[:10]
number_of_primes, example_primes
3.计算m
接下来计算 m m m。这个过程的本质是,求解同余式方程 a 4 ? x 4 ≡ N ? m o d ? p a_4 * x^4 ≡ N\ mod\ p a4??x4≡N?mod?p 并由此构建 m 的值。 m m m 分为两部分:
- 第一部分
m
0
m_0
m0?:
- 根据 Kleinjung 算法的要求,先计算 ( N / a 4 ) 1 / 4 (N/a_4)^{1/4} (N/a4?)1/4,接近于 m m m 的理论值。
- 找到最接近此值且能被 p p p 整除的数作为 m 0 m_0 m0?。
- 第二部分: 满足同余方程解的部分。
- 对于组成 p p p 的每个素数 p i p_i pi?,使用之前从同余方程解集中挑选的解,这些解是为了确保 m m m 满足特定的同余条件 a 4 ? x 4 ≡ N ( m o d p i ) a_4 \cdot x^4 \equiv N \pmod{p_i} a4??x4≡N(modpi?)。
- 将这些解相加得到第二部分的值。
- 计算
m
m
m:
- 将第一部分和第二部分的值相加得到最终的 m m m。
构造多项式 g ( x ) g(x) g(x)
这一步骤是为了构造出多项式
g
(
x
)
=
p
x
?
m
g(x) = px - m
g(x)=px?m。
其中,
p
p
p 是选定的素数乘积,
m
m
m 是通过上述方法计算得到的,确保多项式
g
(
x
)
g(x)
g(x) 满足特定的数学和同余条件。
得到解集
我们首先可以构造出多项式 g ( x ) = p x ? m g(x) = px - m g(x)=px?m,其中 p p p 是选定素数的乘积,而 m m m 是通过以上描述的方法计算得到的。
代码逻辑
- 定义变量:设置 n、p(选定的素数集合)、a_4。
- 计算 P P P: P P P 是选定素数的乘积。
- 解集计算:
- 对每个素数 p i p_i pi?,求解同余方程 a 4 ? x 4 ≡ N ( m o d p i ) a_4 \cdot x^4 \equiv N \pmod{p_i} a4??x4≡N(modpi?)。
- 生成每个 p i p_i pi? 的解集。
n = 1234268228312430759578090015472355712114804731217710966738223
# 需要填入选择的小素数集合和 a_4
p = [17, 157, 181]
a_4 = 1 # 填入 a_4 的值
P = p[0] * p[1] * p[2]
print(f"P: {P}")
# 打印每个小素数同余方程的解集
for i in range(len(p)):
r = n % p[i]
x = []
temp = P // p[i]
tmp = temp
for j in range(1, p[i]):
num = tmp % p[i]
if (a_4 * (num**4)) % p[i] == r:
x.append(tmp)
tmp += temp
print(f"Solutions for p = {p[i]}: {x}")
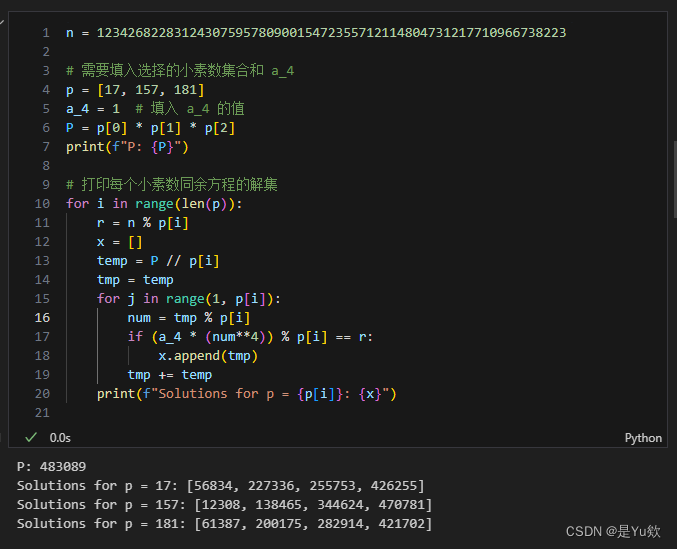
在选择解集中的解时,不同的选择会影响后续多项式低次项系数的确定,特别是 a 3 a_3 a3? 的大小。可以尝试不同的搭配,以使后面的系数尽可能小。
求解m
代码逻辑
- 定义变量:设置 n、p(素数的乘积)、a_4。
- 计算 m 0 m_0 m0?:基于 ( N / a 4 ) 1 / 4 (N/a_4)^{1/4} (N/a4?)1/4 计算 m 0 m_0 m0?。
- 确定 x s o l u t i o n s x_{solutions} xsolutions?:这些选择的解是,从上一步中每个数组里面挑一个。
- 最终计算 m m m:将 m 0 m_0 m0? 和 x s o l u t i o n s x_solutions xs?olutions 的和计算出 m m m 的最终值。
n = 1234268228312430759578090015472355712114804731217710966738223
# 请填入选择的小素数集合和 a_4
a_4 = 1 # 填入 a_4 的值
p = 483089
# 计算第一部分 m0
_m = int((n / a_4)**(1/4))
m0 = int(_m / p) * p + p
# 第二部分:选择的同余方程的解
x_solutions = [56834, 138465, 282914] # 填入从上一步中选择的解,每个数组里面挑一个
# 计算 m
m = m0 + sum(x_solutions)
print(f"p: {p}")
print(f"Calculated value of m: {m}")
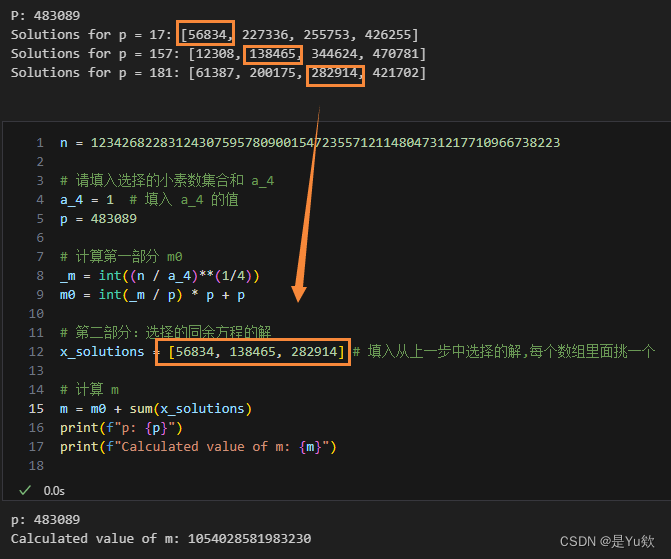
4. 计算多项式系数 a 3 a_3 a3?, a 2 a_2 a2?, a 1 a_1 a1?和 a 0 a_0 a0?,生成多项式
确定完a_4,p,m后,生成并验证多项式。
在这一部分,我们将集中于计算多项式 f ( x ) = a 4 x 4 + a 3 x 3 + a 2 x 2 + a 1 x + a 0 f(x) = a_4x^4 + a_3x^3 + a_2x^2 + a_1x + a_0 f(x)=a4?x4+a3?x3+a2?x2+a1?x+a0? 的系数,并验证所得到的多项式是否正确。
构造多项式 f ( x ) f(x) f(x)
以上步骤允许我们计算出多项式 f ( x ) f(x) f(x) 的所有系数,这个多项式将满足题目中所提出的模 n n n 条件。
代码实现
关键逻辑步骤
- 定义变量:设置
n、p、m以及a_4的值。 - 计算中间变量:为了简化系数的计算,首先计算出若干中间变量,如 p 2 p^2 p2、 p 3 p^3 p3、 p 4 p^4 p4、 m 2 m^2 m2、 m 3 m^3 m3、 m 4 m^4 m4。
- 系数的计算:
- 使用模运算和模逆函数(modular inverse)来逐步计算 a 3 a_3 a3?、 a 2 a_2 a2?、 a 1 a_1 a1? 和 a 0 a_0 a0?。
在 Python 中,可以通过使用 pow 函数来计算模逆,其语法为
pow(a, -1, mod),其中 a 是要求逆的数,mod 是模数。
- 每个系数的计算都基于前一步的结果,以及对应的中间变量。
- 计算 a_3:通过模逆和模运算计算 a 3 a_3 a3?。
- 计算 a_2:进一步利用前面的计算结果和模运算计算 a 2 a_2 a2?。
- 计算 a_1:同样基于之前的结果,计算 a 1 a_1 a1?。
- 计算 a_0:最后计算 a 0 a_0 a0?。
- 验证:通过计算 a 4 m 4 + a 3 m 3 p + a 2 m 2 p 2 + a 1 m p 3 + a 0 p 4 a_4m^4 + a_3m^3p + a_2m^2p^2 + a_1mp^3 + a_0p^4 a4?m4+a3?m3p+a2?m2p2+a1?mp3+a0?p4 并与 n n n 对比来验证结果。
- 验证结果:计算多项式 f ( x ) f(x) f(x) 在 x = m x=m x=m 时的值,并与原始的 n n n 进行对比,以验证多项式的正确性。
n = 1234268228312430759578090015472355712114804731217710966738223
# 填入前面选择的 a_4, p 和 m 的值
a_4 = 1 # 填入 a_4 的值
p = 483089 # 填入 p 的值
m = 1054028581983230 # 填入 m 的值
# 计算所需的中间变量
_m = int((n / a_4)**0.25)
p_2 = p ** 2
p_3 = p ** 3
p_4 = p ** 4
m_2 = m ** 2
m_3 = m ** 3
m_4 = m ** 4
r = n
r = (r - a_4 * m_4) // p
# 计算 a_3
kk1 = r % p
kk2 = pow(m, -1, p) # 模逆
a_3 = (kk1 * (kk2 ** 3)) % p
a_3 -= p
# 计算 a_2
r = (r - a_3 * m_3) // p
a_2 = int((n - a_4 * (_m ** 4)) // (p * p * _m * _m)) - int(_m * (a_4 * 4 * (m - _m) + a_3 * p) // (p * p))
temp = a_2 * m_2
for i in range(p):
if r % p == temp % p:
a_2 += i
break
temp += m_2
# 计算 a_1
r = (r - a_2 * m_2) // p
a_1 = int(r // m)
temp = a_1 * m
for i in range(p):
if r % p == temp % p:
a_1 += i
break
temp += m
# 计算 a_0
r = (r - a_1 * m) // p
a_0 = r
# 验证结果
num = a_4 * m_4 + a_3 * m_3 * p + a_2 * m_2 * p_2 + a_1 * m * p_3 + a_0 * p_4
print(f"Calculated: {num}, Original: {n}")
print(f"p: {p}, m: {m}, a_4: {a_4}, a_3: {a_3}, a_2: {a_2}, a_1: {a_1}, a_0: {a_0}")
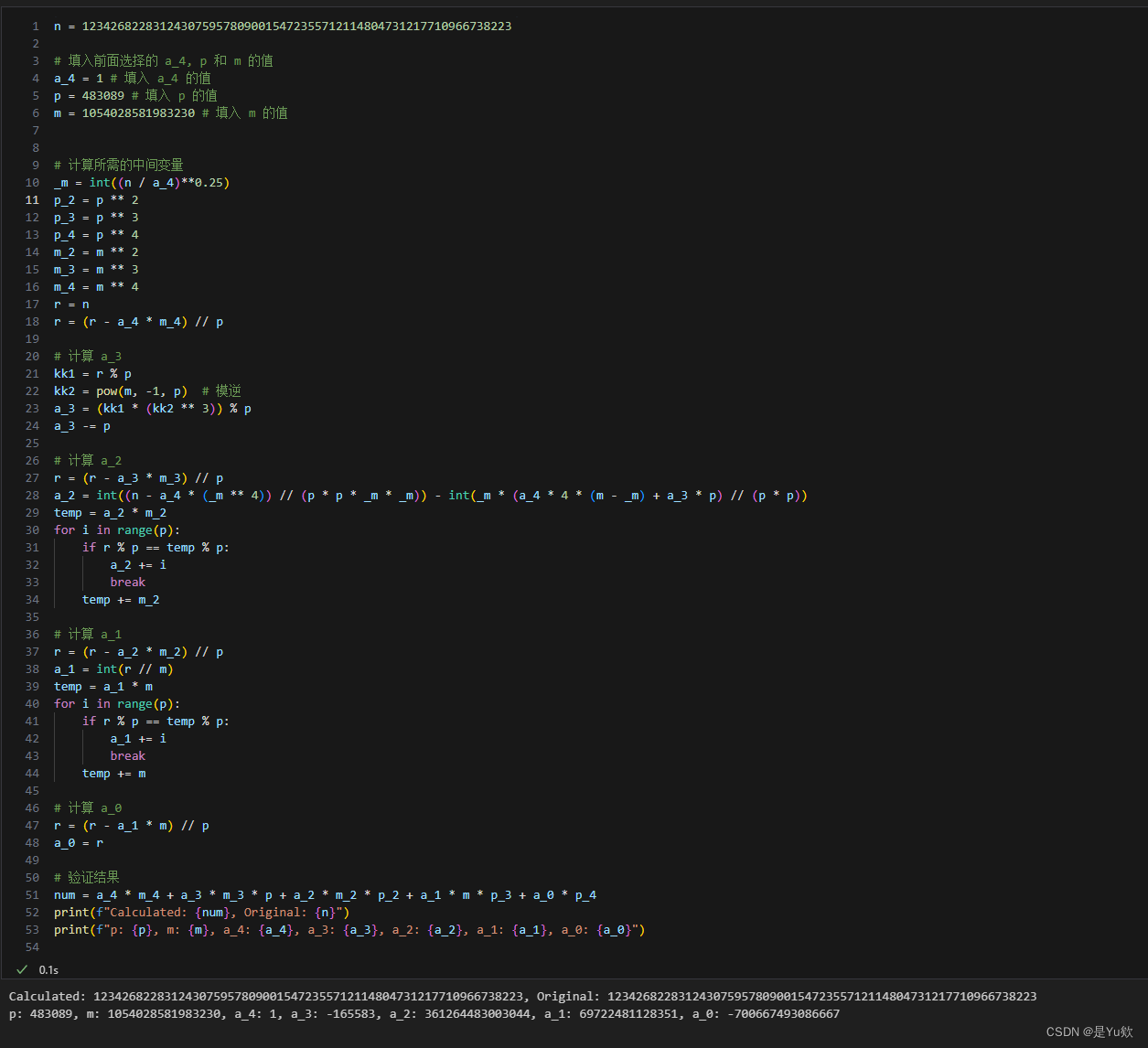
注意验证检查时重点看一下最后几位数,我前面输入有问题时,最后5位数字对不上,说明整数分解错误。
Calculated: 1234268228312430759578090015472355712114804731217710966738223, Original: 1234268228312430759578090015472355712114804731217710966738223
p: 483089, m: 1054028581983230, a_4: 1, a_3: -165583, a_2: 361264483003044, a_1: 69722481128351, a_0: -700667493086667
如果报错:ValueError: base is not invertible for the given modulus
在尝试计算 m 的模逆时出现了问题,报错ValueError: base is not invertible for the given modulus
原因: m 和 p 不互质,即它们有共同的因子。在这种情况下,模逆并不存在。
因此,为了解决这个问题,我们需要确保 m 和 p 是互质的。
如果它们不是互质的,可能需要重新选择解集,检查 m 的值或 p 的值是否正确。
5. 计算 COUNT 并选择最优的 A/B
在这一部分,我们将专注于选择最优的 A / B A/B A/B 比例并计算相应的 C O U N T COUNT COUNT。 C O U N T COUNT COUNT 是满足特定条件的点对 ( a , b ) (a,b) (a,b) 的数量,其中 a ∈ [ ? A , A ] a \in [-A,A] a∈[?A,A], b ∈ [ 1 , B ] b \in [1, B] b∈[1,B]。这一计算涉及到,验证两个表达式是否可以由小于 100000 的素数完全分解。
但请注意,由于代码涉及大量的质因数分解,因此计算复杂度很高,尤其是在较大数值范围内。
代码实现
在 Python 中,我们可以使用 sympy 库来获取一个数的质因数。
代码1(时间过长中断运行了,58min运行了5%-1160min)
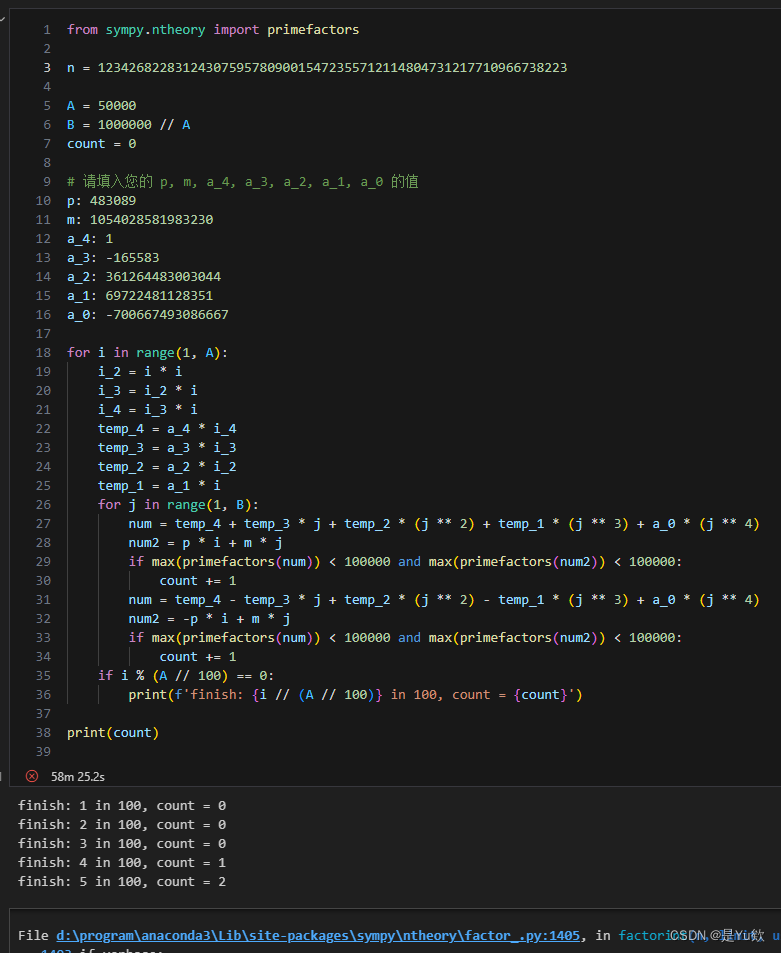
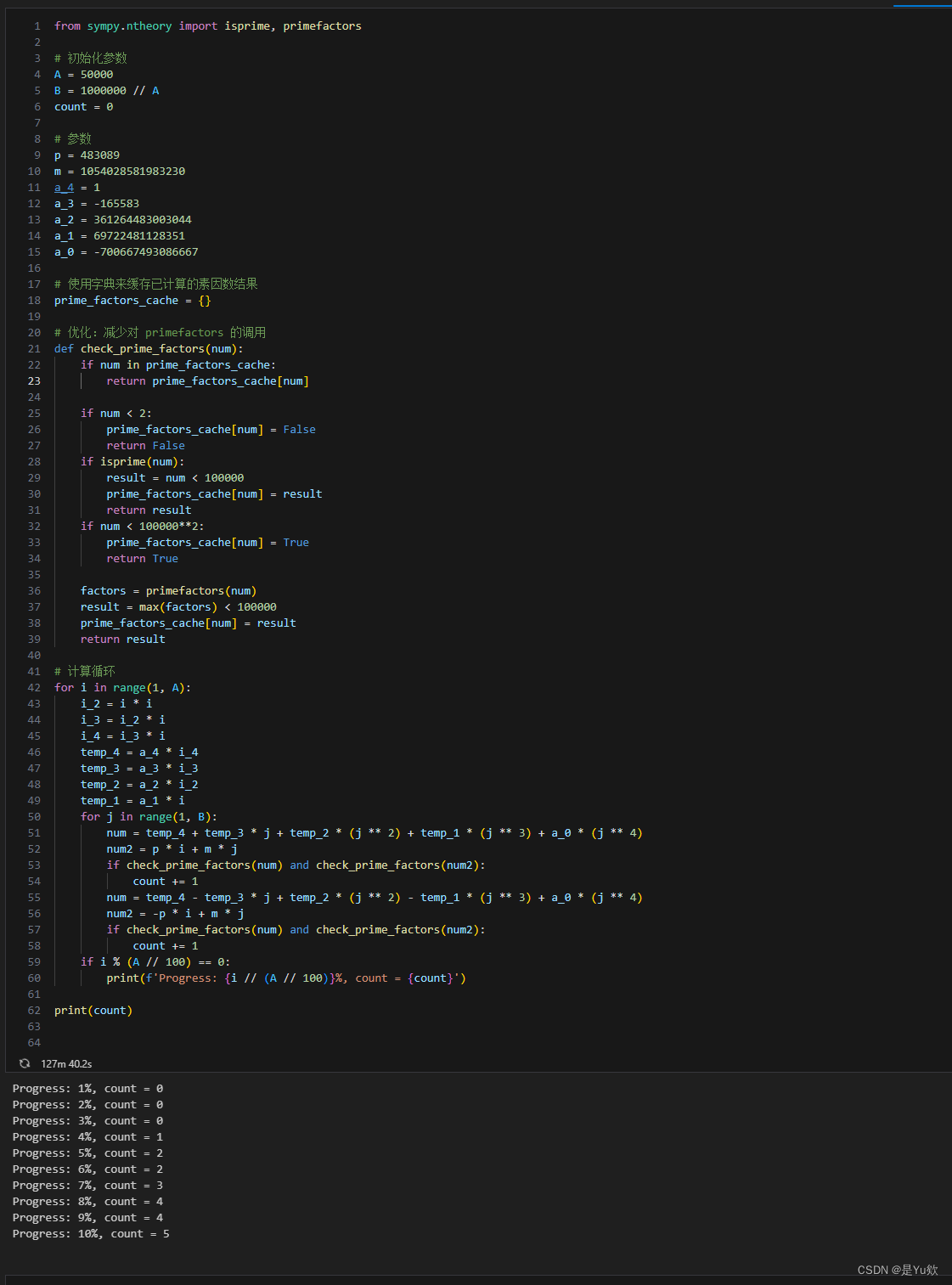
代码优化1(127min运行了10%)
这段代码的主要瓶颈在于它对于每个 num 和 num2 都调用了 primefactors 函数,这是一个非常耗时的操作,特别是当数值很大时。
思路:首先将优化代码的重点,放在减少对 primefactors 的调用和避免重复计算上。
-
减少对
primefactors函数的调用:我们可以在进行因数分解之前,先用一些简单的方法来筛选掉一些显然不满足条件的数。比如,检查是否为平方数or其他简单因数的倍数,检查数字是否小于100000的平方(因为这是我们对因数的最大限制)。 -
避免重复计算:在双重循环中,有些乘法操作是重复的,可以将它们移到循环外进行一次性计算。
-
分批处理和间隔检查:可以考虑将计算过程分批进行,并在每批之后进行一次间隔检查,以此来减轻计算压力。
-
内存优化:注意到
precomputed列表可能会占用大量内存,尤其是在 A 很大的情况下。可以考虑只存储必要的值,或者在不再需要时及时清除内存。
为了优化这个过程,我们可以采取以下策略:
-
生成素数列表:首先生成一个小于 100,000 的素数列表。这样,我们就可以在检查每个
num和num2时,只检查这些素数,而不是对每个数都进行完整的因数分解。 -
优化因数分解:我们可以编写一个自定义的因数分解函数,该函数仅考虑小于 100,000 的素数。这样,我们就避免了在大数上执行全面的因数分解,从而大大减少了计算量。
-
避免重复计算:通过存储中间结果来减少重复计算。例如,我们可以在循环外部计算
i的幂,并在循环内部重用这些值。 -
限制因数分解的深度:在
can_be_fully_decomposed_by_small_primes函数中,如果num在除以一个小素数之后变得非常大(比如大于 100,000 的平方),则可以立即返回 False,因为此时num显然不能被小于 100,000 的素数完全分解。
代码优化2(33min)
算法分析:决定哪种算法最适合优化(遗传算法、递归算法、√ 动态规划)
针对这个特定的问题,我们首先需要理解其数学和计算上的本质,以决定哪种算法最适合优化。这段代码的主要任务是找出一组特定条件下的数值,并检查这些数值的最大素因数是否小于100000。根据这个目标,我们可以评估以下几种算法的适用性:
-
遗传算法:通常用于优化和搜索问题,特别是在解空间巨大且不确定的情况下。然而,遗传算法更适用于那些没有明确解析解的问题,而在这种情况下,我们面临的是一个具有明确计算步骤的数学问题。
-
递归算法:递归算法适用于可以分解为较小、重复的子问题的情况。在当前的问题中,我们并没有明显的递归结构,因此递归算法可能不是最佳选择。
-
动态规划算法:动态规划适用于解决具有重叠子问题和最优子结构的问题。对于当前问题,如果能够识别出重叠的子问题,并且这些子问题的解可以用来构建整体解,则动态规划可能是一个有效的选择。
考虑到这些因素,看起来动态规划可能是三者中最有希望的选择,尤其是如果我们能够将问题重构为一个具有最优子结构的形式。然而,对于当前的具体问题,我们需要深入分析和理解其数学性质,以确定是否真的存在这样的子结构。
针对原有代码的优化,我们可以尝试以下策略:
- 缓存和重用计算结果:这是一种简化动态规划的方法,其中我们缓存之前计算的结果以避免重复计算。
- 避免不必要的计算:仔细分析数学表达式和逻辑,看是否有计算步骤可以省略或简化。
最后,引入了一个缓存机制来减少对 primefactors 函数的调用次数。
关键步骤
- 初始化参数:设置 A A A、 B B B、 p p p、 m m m 以及多项式 f ( x ) f(x) f(x) 的系数。
- 生成素数列表:创建小于 100000 的素数列表。
- 定义分解函数:
can_be_fully_decomposed_by_small_primes函数检查一个数是否可以由小于 100000 的素数完全分解。 - 计算循环:
- 遍历 ( a , b ) (a,b) (a,b) 对,并计算 b 4 f ( a b ) b^4f\left(\frac{a}{b}\right) b4f(ba?) 和 b g ( a b ) bg\left(\frac{a}{b}\right) bg(ba?)。
- 检查这两个值是否都能由小于 100000 的素数完全分解。
- 如果可以,增加 C O U N T COUNT COUNT。
代码逻辑
- 循环遍历:对于每个 a ∈ [ ? A , A ] a \in [-A,A] a∈[?A,A] 和 b ∈ [ 1 , B ] b \in [1, B] b∈[1,B],计算相应的表达式。
- 分解检查:使用自定义的分解函数检查两个表达式是否都能被完全分解。
- 统计 COUNT:记录满足条件的点对的数量。
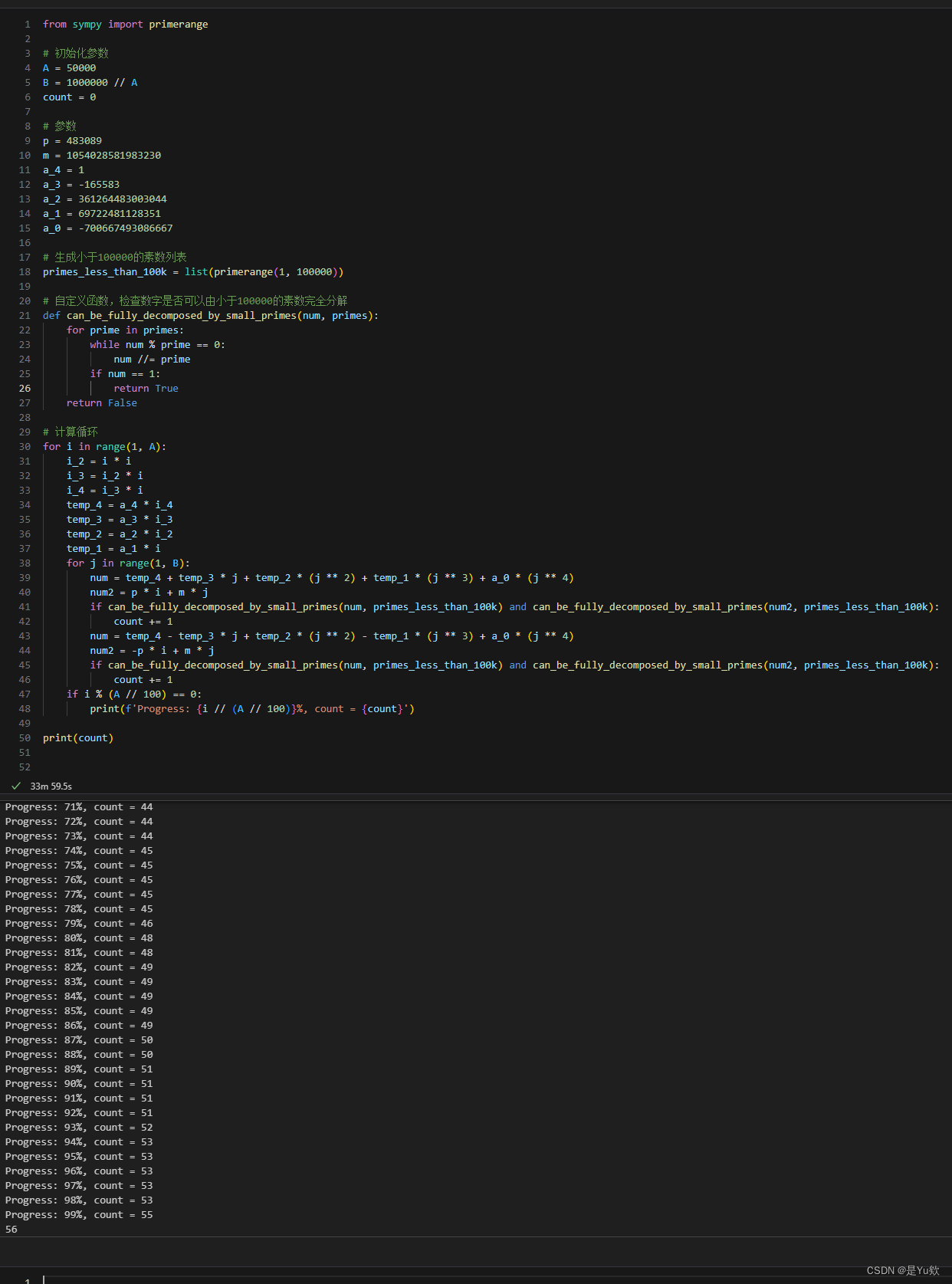
from sympy import primerange
# 初始化参数
A = 50000
B = 1000000 // A
count = 0
# 参数
p = 483089
m = 1054028581983230
a_4 = 1
a_3 = -165583
a_2 = 361264483003044
a_1 = 69722481128351
a_0 = -700667493086667
# 生成小于100000的素数列表
primes_less_than_100k = list(primerange(1, 100000))
# 自定义函数,检查数字是否可以由小于100000的素数完全分解
def can_be_fully_decomposed_by_small_primes(num, primes):
for prime in primes:
while num % prime == 0:
num //= prime
if num == 1:
return True
return False
# 计算循环
for i in range(1, A):
i_2 = i * i
i_3 = i_2 * i
i_4 = i_3 * i
temp_4 = a_4 * i_4
temp_3 = a_3 * i_3
temp_2 = a_2 * i_2
temp_1 = a_1 * i
for j in range(1, B):
num = temp_4 + temp_3 * j + temp_2 * (j ** 2) + temp_1 * (j ** 3) + a_0 * (j ** 4)
num2 = p * i + m * j
if can_be_fully_decomposed_by_small_primes(num, primes_less_than_100k) and can_be_fully_decomposed_by_small_primes(num2, primes_less_than_100k):
count += 1
num = temp_4 - temp_3 * j + temp_2 * (j ** 2) - temp_1 * (j ** 3) + a_0 * (j ** 4)
num2 = -p * i + m * j
if can_be_fully_decomposed_by_small_primes(num, primes_less_than_100k) and can_be_fully_decomposed_by_small_primes(num2, primes_less_than_100k):
count += 1
if i % (A // 100) == 0:
print(f'Progress: {i // (A // 100)}%, count = {count}')
print(count)
最大化收益率
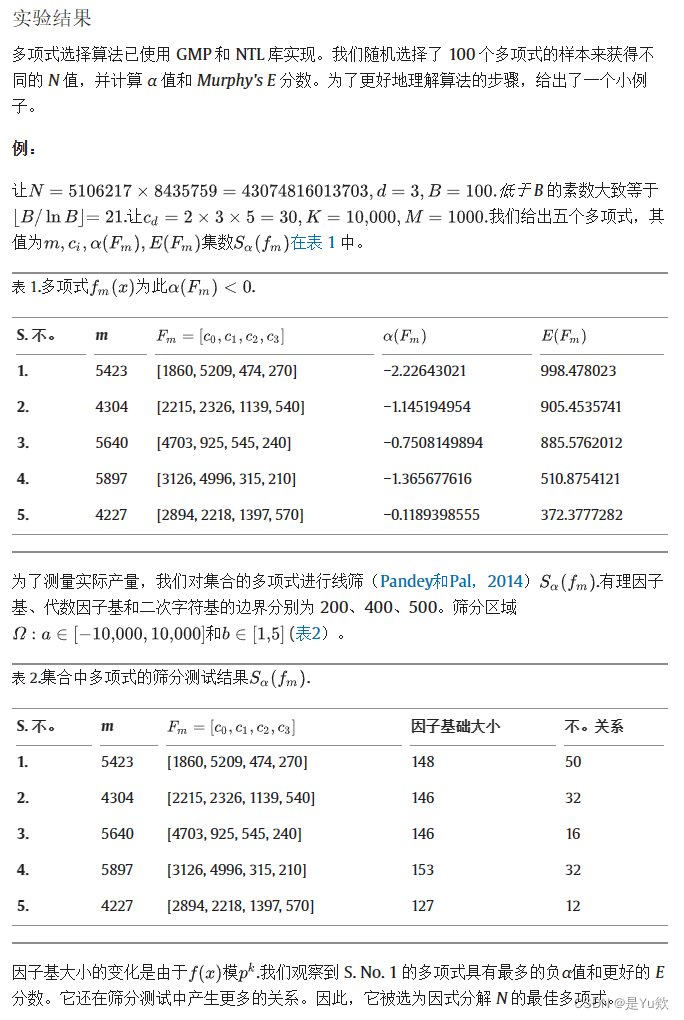
收益率百分比衡量的是使用选定的多项式对成功实现因子分解的比例,相对于因子分解尝试的总数。
本质上,较高的收益百分比反映了GNFS算法中选择部署的多项式对的质量。它表示这些多项式有效地促进大整数因子分解的能力,最终影响因子分解过程的整体性能和成功率,反映了所选多项式产生可行因子分解结果的能力。
因此,在GNFS算法的多项式选择中,获得更高的收益率是一个关键目标,因为它直接与算法高效和成功地因子化大整数的能力相关。
计算 COUNT 和优化 A/B
这个代码段将帮助我们确定在给定参数下 C O U N T COUNT COUNT 的值,并且可以通过调整 A A A 和 B B B 的值来寻找最大化 C O U N T COUNT COUNT 的最优比例。
- 实验和分析:通过不同的 A A A 和 B B B 值进行实验,观察 C O U N T COUNT COUNT 的变化。
- 分析影响因素:探索 s k e w = A B skew = \frac{A}{B} skew=BA? 和系数 c 4 c_4 c4? 如何影响 C O U N T COUNT COUNT,以及如何调整这些参数以优化结果。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 解决IDEA自动生成返回值带有final修饰的问题
- Tortoise-orm 使用(三) 一对一,一对多,多对多关系表及操作
- 牛客周赛 Round 17 解题报告 | 珂学家 | 枚举贪心 + 二分最短路
- ICC2:先进工艺pin access相关app option
- 软件测试/测试开发丨Pytest结合数据驱动-CSV
- Java版商城:Spring Cloud+SpringBoot b2b2c实现多商家入驻、直播带货及免 费小程序商城搭建
- 运营人必备的运营策略:实现业务增长的关键步骤
- 【形式语言与自动机/编译原理】CFG-->Greibach-->NPDA(2)
- 日期类的实现|运算符重载的复用
- Linux之IP地址、主机名、域名解析