牛客周赛 Round 17 解题报告 | 珂学家 | 枚举贪心 + 二分最短路

---

前言

---

整体评价

其实T3最有意思， T4很典，是一道二分+最短路径经典套路。

T3 如果尝试 增量差值最小 的最大梯度去贪心的话，会失败，需要切换思路。

珂朵莉 牛客周赛专栏

珂朵莉 牛客小白月赛专栏

---

A. 游游的正方形披萨

如果横竖差值最小的话

两者要么相等，要么差一

令 e1 = n / ((k + 1)/2+1), e2 = n / (k/2 + 1)

则 s = e1 * e2

这样很好的兼顾了k为奇偶的情况

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        int n = sc.nextInt();
        int k = sc.nextInt();

        double e1 = n * 1.0 / ((k + 1)/2 + 1);
        double e2 = n * 1.0 / (k/2 + 1);
        double s = e1 * e2;
        System.out.printf("%.2f\n", s);
    }

}

---

B. 游游的字母翻倍

这题字符串和操作次数较小，然后可以暴力模拟

如果操作数很多的话，可能需要借助数据结构来维护增量

因为这里面有明显的区间操作.

import java.io.BufferedInputStream;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        int n = sc.nextInt();
        int q = sc.nextInt();

        char[] str = sc.next().toCharArray();

        for (int i = 0; i < q; i++) {
            int l = sc.nextInt() - 1, r = sc.nextInt() - 1;
            int d = r - l + 1;
            char[] str2 = new char[str.length + d];

            // 头部
            System.arraycopy(str, 0, str2, 0,l);

            // 中间的double
            for (int j = 0; j < d; j++) {
                str2[l + j * 2] = str2[l + j * 2 + 1] = str[j + l];
            }

            // 尾巴
            System.arraycopy(str, r + 1, str2, r + 1 + d, str.length - (r + 1));
            str = str2;
        }

        System.out.println(new String(str));

    }

}

---

C. 数组平均

这题很有意思，先来看一个显而易见的结论

• k == 1, 则结果为 最大值 - 最小值
• k == n, 则结果必然为 0

如果核心的焦点在于， k在两者之间时，如何求解

一开始猜了一个，从收益最大(差值减少梯度)的角度去贪心，结果WA，而且得分不高

一度没辙，后面仔细分析了下，感觉可以枚举最大的没有被选中的项

如果选中某一个项为最大值，那比它小，而离的越近必然被保留，所以k的选择一定分布在前后缀.

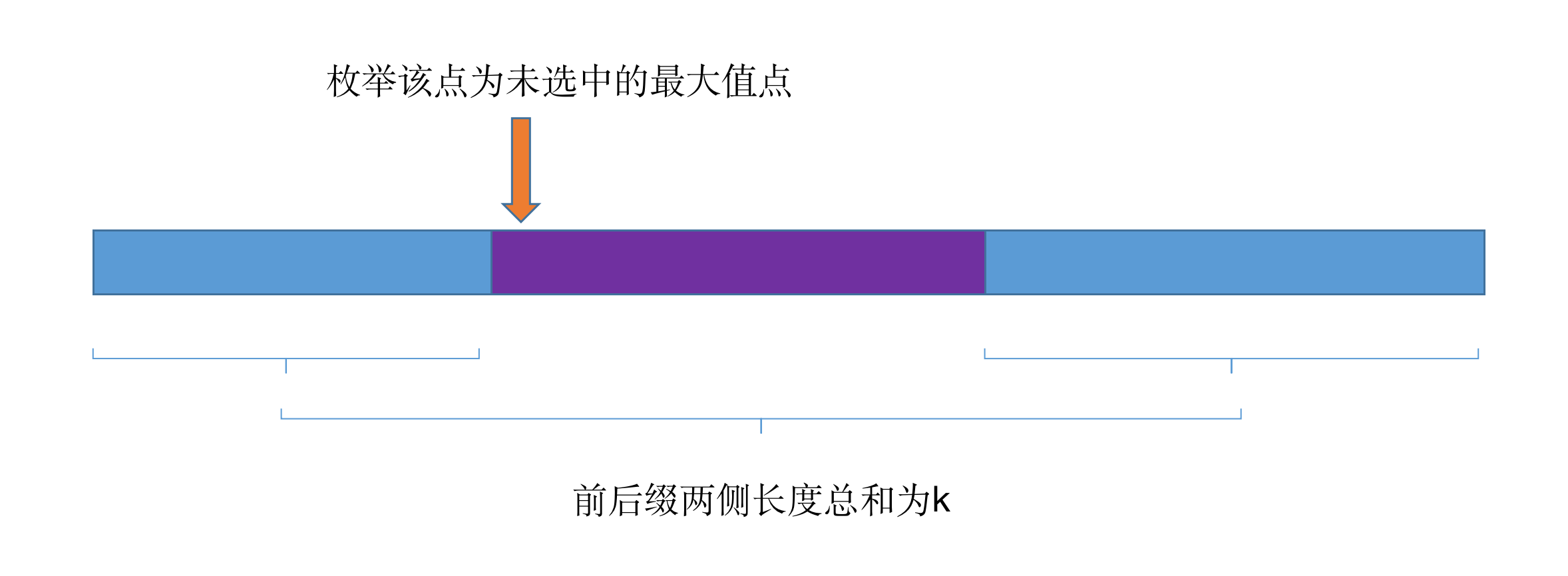
所以思路是

• 排序
• 枚举未被选中的最大值
• 利用前后缀优化加速

import java.io.*;
import java.util.*;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));
        int n = sc.nextInt(), k = sc.nextInt();
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = sc.nextInt();
        }

        Arrays.sort(arr);
        if (k == 1) {
            System.out.println(arr[n - 1] - arr[0]);
        } else if (k == n) {
            System.out.println(0);
        } else {
            double ans = arr[n - 1] - arr[0];
            // 前后缀拆解
            long[] suf = new long[n + 1];
            for (int j = n - 1; j >= 0; j--) {
                suf[j] = suf[j + 1] + arr[j];
            }

            long pre = 0;
            // 假设这个元素没被选中
            for (int i = 0; i < n; i++) {
                if (i > k) break;
                long acc = pre + suf[n + i - k];
                double avg = acc * 1.0 / k;
                double m1 = Math.max(avg, arr[n + i - k - 1]);
                double m2 = Math.min(avg, arr[i]);

                ans = Math.min(ans, m1 - m2);
                pre += arr[i];
            }

            System.out.println(ans);
        }
    }

}

---

D. 游游出游

经典套路题

二分最大重量，然后check逻辑中跑最短路(Dijkstra)进行验证

import java.io.*;
import java.util.*;

public class Main {

    static long inf = Long.MAX_VALUE / 10;

    static boolean check(int n, List<int[]> []g, int limit, int h) {

        long[] res = new long[n];
        Arrays.fill(res, inf);

        PriorityQueue<long[]> pq = new PriorityQueue<>(Comparator.comparing(x -> x[1]));
        pq.offer(new long[] {0, 0});
        res[0] = 0;

        while (!pq.isEmpty()) {
            long[] cur = pq.poll();
            int u = (int)cur[0];
            if (cur[1] > res[u]) continue;

            for (int[] e: g[u]) {
                int v = e[0];
                if (e[1] >= limit && res[v] > res[u] + e[2]) {
                    res[v] = res[u] + e[2];
                    pq.offer(new long[] {v, res[v]});
                }
            }
        }

        return res[n - 1] <= h;
    }


    public static void main(String[] args) {
        Scanner sc = new Scanner(new BufferedInputStream(System.in));

        int n = sc.nextInt(), m = sc.nextInt(), h = sc.nextInt();

        // 二分
        List<int[]>[]g = new List[n];
        Arrays.setAll(g, x -> new ArrayList<>());

        int mz = 0;
        for (int i = 0; i < m; i++) {
            int u = sc.nextInt() - 1, v = sc.nextInt() - 1;
            int w = sc.nextInt(), d = sc.nextInt();

            g[u].add(new int[] {v, w, d});
            g[v].add(new int[] {u, w, d});

            mz = Math.max(mz, w);
        }

        int l = 0, r = mz;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if (check(n, g, mid, h)) {
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        System.out.println(r);

    }

}

---

写在最后