124 二叉树中的最大路径和
发布时间:2024年01月06日
又是一个hard题目,其实我大概有想到要去dfs遍历节点,当时不知道怎么从一个叶子结点开始遍历。其实只需要从根节点出发,看看左右节点加在一起是否最大能不能作为一个路径,但是对外这是要不左节点上来要不右节点上来,不能两个结点都上来要不然会重复
题目
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:
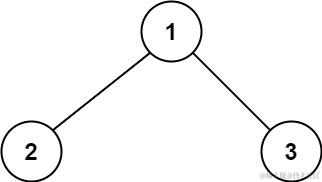
输入: root = [1,2,3]
输出: 6
解释: 最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
代码与解析
代码上有注释,详细的思路解答
class Solution {
int maxSum = Integer.MIN_VALUE; // 用于记录最大路径和
/**
* 计算二叉树中任意节点的最大路径和
* @param root 给定的二叉树根节点
* @return 返回最大路径和
*/
public int maxPathSum(TreeNode root) {
// 如果树只有一个节点,则直接返回该节点的值
if(root.left == null && root.right == null) return root.val;
// 调用深度优先搜索方法
dfs(root);
return maxSum;
}
/**
* 深度优先搜索计算路径和
* @param node 当前节点
* @return 返回当前节点向下路径和的最大值
*/
public int dfs(TreeNode node) {
if(node == null) return 0; // 空节点返回0
int l = Math.max(dfs(node.left), 0); // 左子树提供的最大路径和,负值设为0
int r = Math.max(dfs(node.right), 0); // 右子树提供的最大路径和,负值设为0
int innerMax = l + r + node.val; // 当前子树内部的最大路径和
maxSum = Math.max(maxSum, innerMax); // 更新最大路径和
int outSum = node.val + Math.max(0, Math.max(l, r)); // 当前节点向上提供的最大路径和
return outSum < 0 ? 0 : outSum; // 若对外提供的路径和为负,返回0;否则返回路径和
}
}
文章来源:https://blog.csdn.net/m0_51547272/article/details/135423526
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 你知道海外云手机可以用于外贸测评吗?
- 软考13-上午题-程序设计语言概述
- linux---网络
- K8S学习指南(68)-开发自定义控制器
- 创建第一个SpringMVC项目,入手必看!
- 面试Java岗老喜欢盯着JVM问,有那么多项目要调优吗?
- MIPS32 cache初始化
- 算法训练营第五十六天|583. 两个字符串的删除操作 72. 编辑距离
- HTML--CSS--边框、列表、表格样式
- Github Copilot AI保密级教程