Python实现两因素独立设计方差分析,简单效应分析
#?Python实现两因素独立设计方差分析
1. 背景
1. 有研究者探讨了在不同企业文化下,管理者的不同语言风格所产生的影响
有的企业注重员工的独立性,强调个人努力和内部竞争;有的企业注重员工的整体性,强调团队合作和团队绩效。
管理者的语言风格有斩钉截铁型和优柔寡断型。
据此,研究者制作了 4 种录音材料,分别提供不同企业文化背景下管理者不同语言风格的对话内容, 12名被试被分成4组参与了实验,每组分别听不同的录音。最后要求被试用 7 点量表评估管理者的能力。
结果如下:
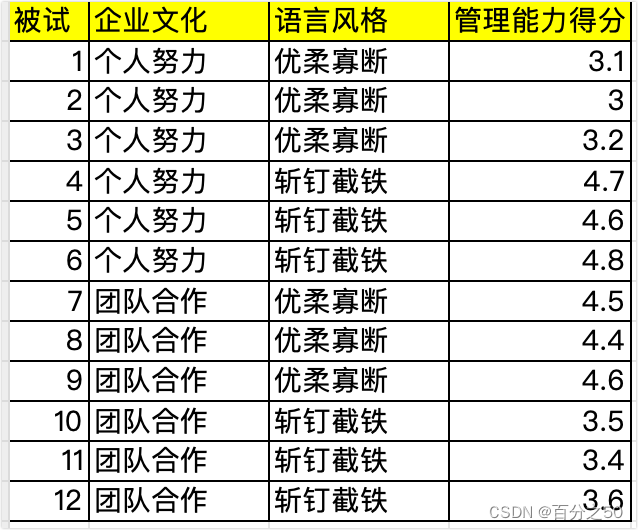
实验目的:探究不同企业文化下不同语言风格对管理能力得分的影响。
实验设计:2*2 两因素独立方差分析
变量:
自变量1: 企业文化(个人努力VS团队合作),自变量2: 语言风格(优柔寡断VS斩钉截铁)
因变量:管理能力得分
PS:此处为了减少数据转换操作,故直接采用长数据格式。
2. Python代码
import pandas as pd
from statsmodels.stats.multicomp import pairwise_tukeyhsd
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
from scipy import stats
def general_data():
# 为了减少转换这里直接给了长数据,指定第0列(表中第1列)为索引列
df_two_way = pd.read_excel('./excel/不同企业文化下不同语言风格对管理的影响.xlsx', index_col=0)
print("df_two_way=\n", df_two_way)
# 制定各列的变量名,如不指定则直接用表头
# df_two_way.columns = ['企业文化', '语言风格', '管理能力得分']
return df_two_way
def two_way_anova(df_two_way):
# 包括两个主效应和一个交互效应
formula = '管理能力得分 ~ C(企业文化) + C(语言风格) + C(企业文化) : C(语言风格)'
model_two_way = ols(formula, df_two_way).fit()
anova_table = anova_lm(model_two_way)
print("=======输出方差分析表=======")
# print(anova_table)
for i in range(3): # 将科学计数法转换为小数并只保留3位小数,和SPSS输出结果一致
anova_table["PR(>F)"][i] = format(anova_table["PR(>F)"][i], ".3f")
print(anova_table)
# 读取交互效应行,如果显著,进行下一步,简单效应分析
int_p = anova_table["PR(>F)"]["C(企业文化):C(语言风格)"]
print("交互作用p值=", int_p)
if float(int_p) < 0.05:
print("p值小于0.05,交互效应显著,要进行简单效应分析")
return True
# 由于没有找到现成的方案,所以考虑对表格进行拆分,如果交互作用显著,
# 则读取表格中的某一变量的某个水平下的所有数据,然后进行t校验
# 这是自己写的一个简单的算法,如有更好的方法欢迎赐教
def simple_effect_analysis(check, melt_data):
dependent = "管理能力得分"
# 交互效应存在,进行简单效应分析,否则跳过
if check:
# 简单效应分析需要分别
# 检测企业文化为"个人努力"下的不同语言风格差异,
# 以及企业文化为"团队合作"下的不同语言风格差异,
# 分别对两种情况进行t检验即可
groups = melt_data.groupby(melt_data.企业文化)
for company_culture in ["个人努力", "团队合作"]:
melt_data = groups.get_group(company_culture)
# print(melt_data)
# 分别比较在不同企业文化下,不同语言风格对管理能力得分影响的差异
print("\n=======%s企业文化下不同语言风格t检验分析结果=========" % company_culture)
t_test(melt_data)
def t_test(melt_data):
melt_data = melt_data[['语言风格', '管理能力得分']]
# print("melt_data=\n", melt_data)
groups = melt_data.groupby(melt_data.语言风格)
a_group = groups.get_group("优柔寡断")
# print("a_group=\n", a_group)
b_group = groups.get_group("斩钉截铁")
# print("b_group=\n", b_group)
t_value, p_value = stats.ttest_ind(a=a_group['管理能力得分'], b=b_group['管理能力得分'])
# T = (样本均值 - 总体均值或另一样本均值) / (标准误差)
print(f"T值:{t_value:.3f}, p值:{p_value:.3f}")
data = general_data()
simple_effect_analysis(two_way_anova(data), data)
3. 结果
3.1 运行以上代码,会出现如下结果
3.1.1 两因素独立方差分析输出结果
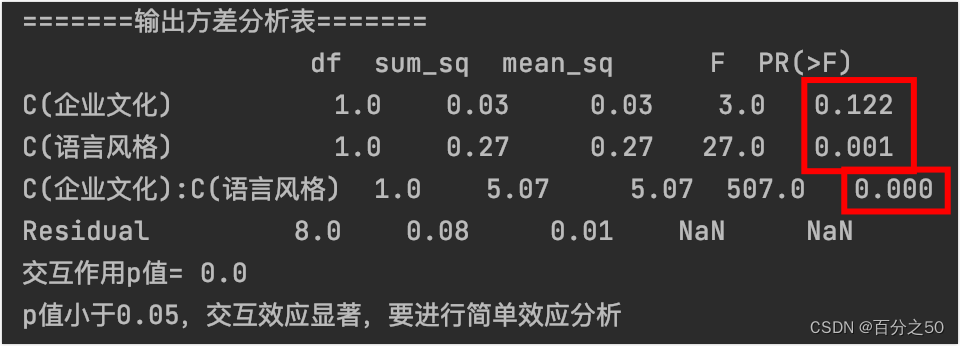
由于它这里对得不是很齐,所以我把p值圈了出来,可以看到有两个主效应的p值和一个交互效应的p值,其中企业文化主效应不显著,其他两个显著。
我的代码检测到交互作用p值小于0.05,就自动进入简单效应分析。
可以和SPSS的输出结果对比下:
中文版:
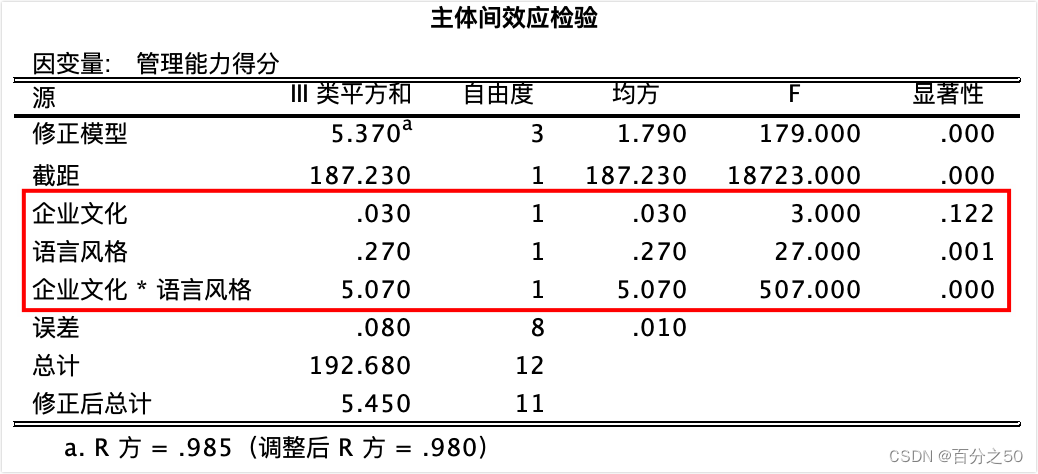
英文版:
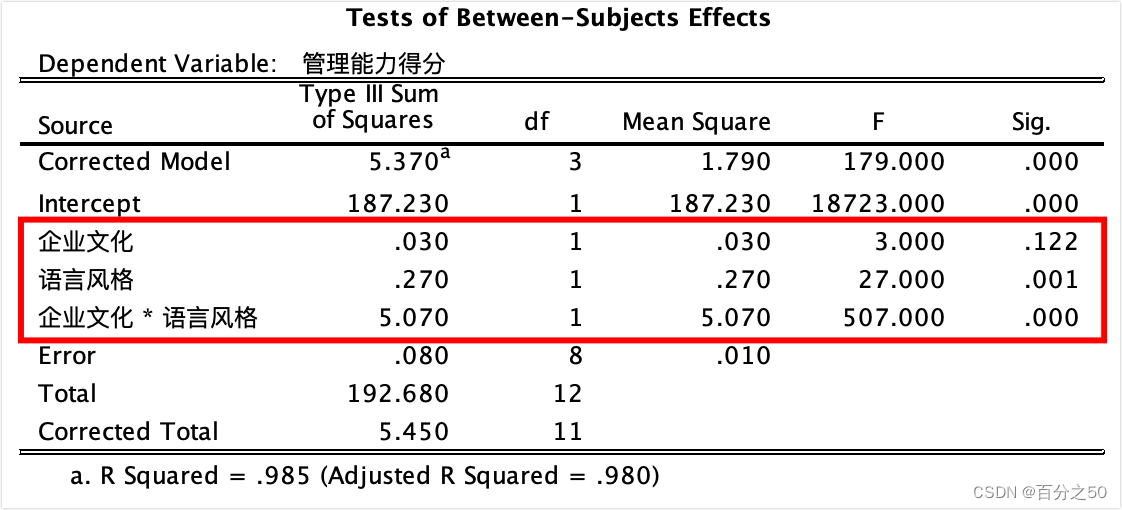
3.1.2 简单效应分析结果
由于没有找到现成的方案来做简单效应分析,所以考虑对表格进行拆分,如果交互作用显著,则读取表格中的某一变量的某个水平下的所有数据,然后进行t检验。 代码中呈现的是自己写的简单算法,如有错误或更好的方法欢迎赐教。
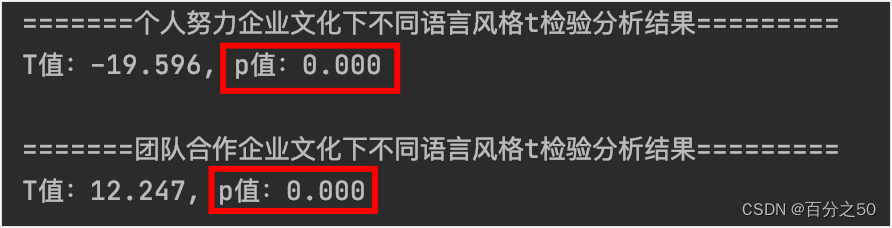
补充,T值的公式为:
T = (样本均值 - 总体均值或另一样本均值) / (标准误差)
SPSS中的输出:
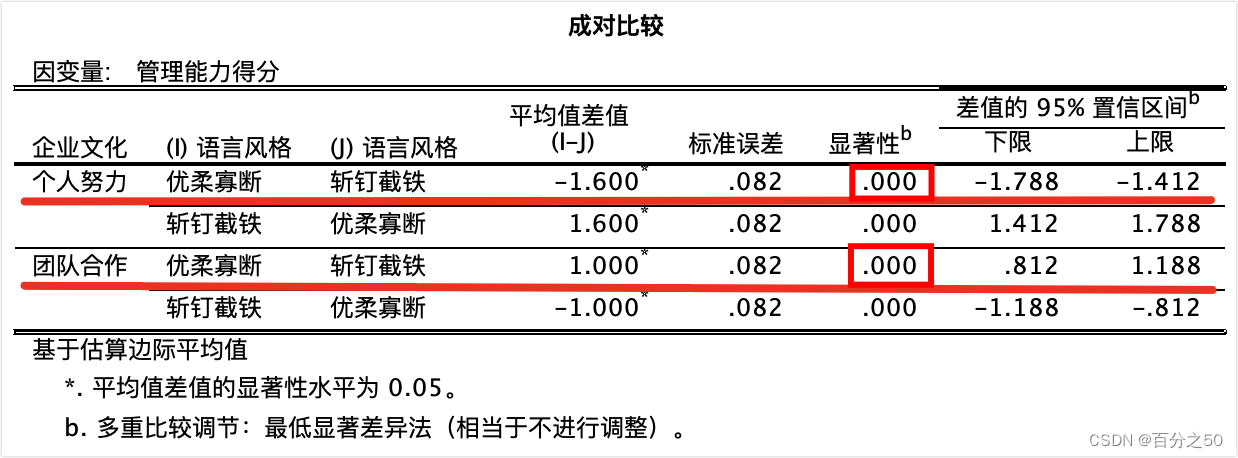
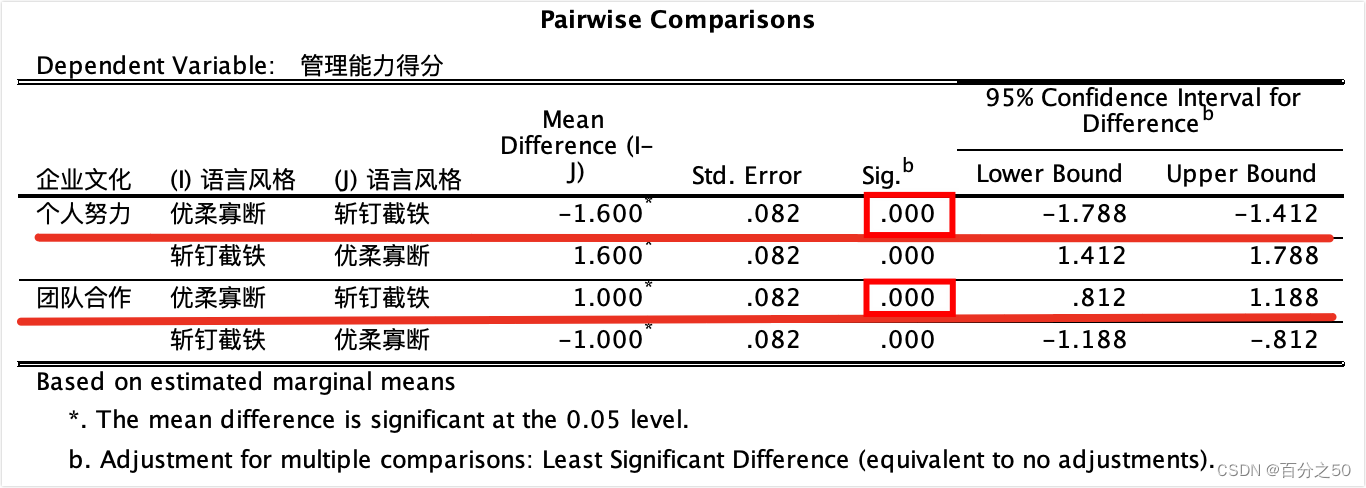
这里SPSS是采用了语法编辑器中的COMPARE语句,因为没有直接的成对比较方法。
可以看出,在不同企业文化下,不同语言风格的管理能力得分均存在显著差异。
4. 详细分析
4.1 方差分析
4.1.1 python代码
def general_data():
# 为了减少转换这里直接给了长数据,指定第0列(表中第1列)为索引列
df_two_way = pd.read_excel('./excel/不同企业文化下不同语言风格对管理的影响.xlsx', index_col=0)
print("df_two_way=\n", df_two_way)
# 制定各列的变量名,如不指定则直接用表头
# df_two_way.columns = ['企业文化', '语言风格', '管理能力得分']
return df_two_way
def two_way_anova(df_two_way):
# 包括两个主效应和一个交互效应
formula = '管理能力得分 ~ C(企业文化) + C(语言风格) + C(企业文化) : C(语言风格)'
model_two_way = ols(formula, df_two_way).fit()
anova_table = anova_lm(model_two_way)
print("=======输出方差分析表=======")
# print(anova_table)
for i in range(3): # 将科学计数法转换为小数并只保留3位小数,和SPSS输出结果一致
anova_table["PR(>F)"][i] = format(anova_table["PR(>F)"][i], ".3f")
print(anova_table)
# 读取交互效应行,如果显著,进行下一步,简单效应分析
int_p = anova_table["PR(>F)"]["C(企业文化):C(语言风格)"]
print("交互作用p值=", int_p)
if float(int_p) < 0.05:
print("p值小于0.05,交互效应显著,要进行简单效应分析")
return True
代码中都有详细注释,不再重复,这里补充一下SPSS操作
4.1.2 SPSS操作
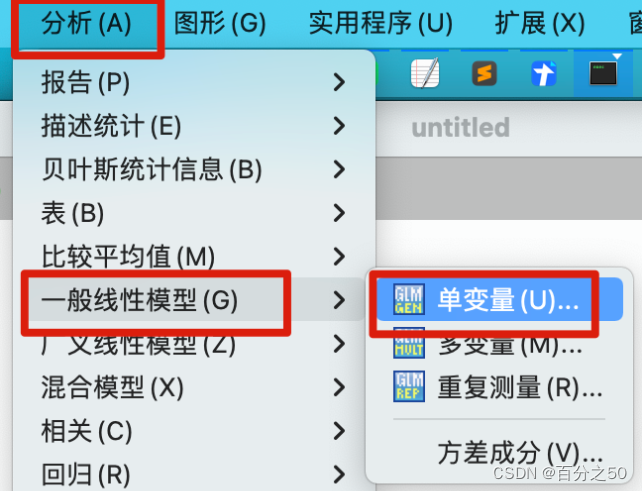
把自变量和因变量放入对应位置,点击确认即可
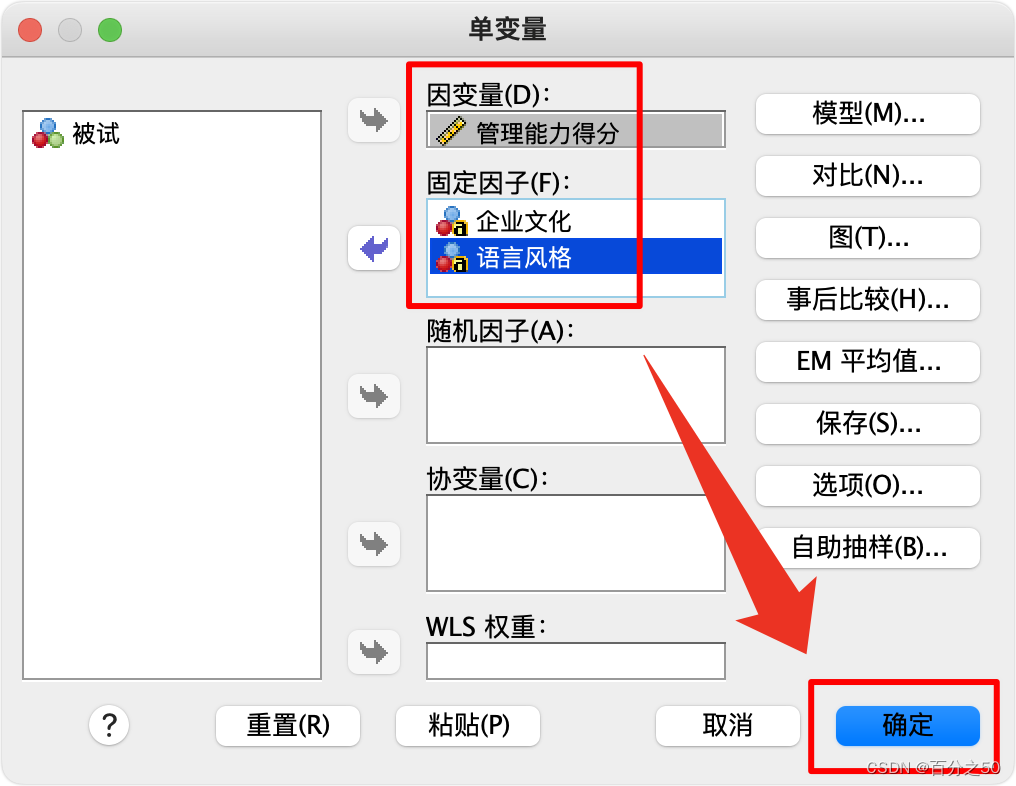
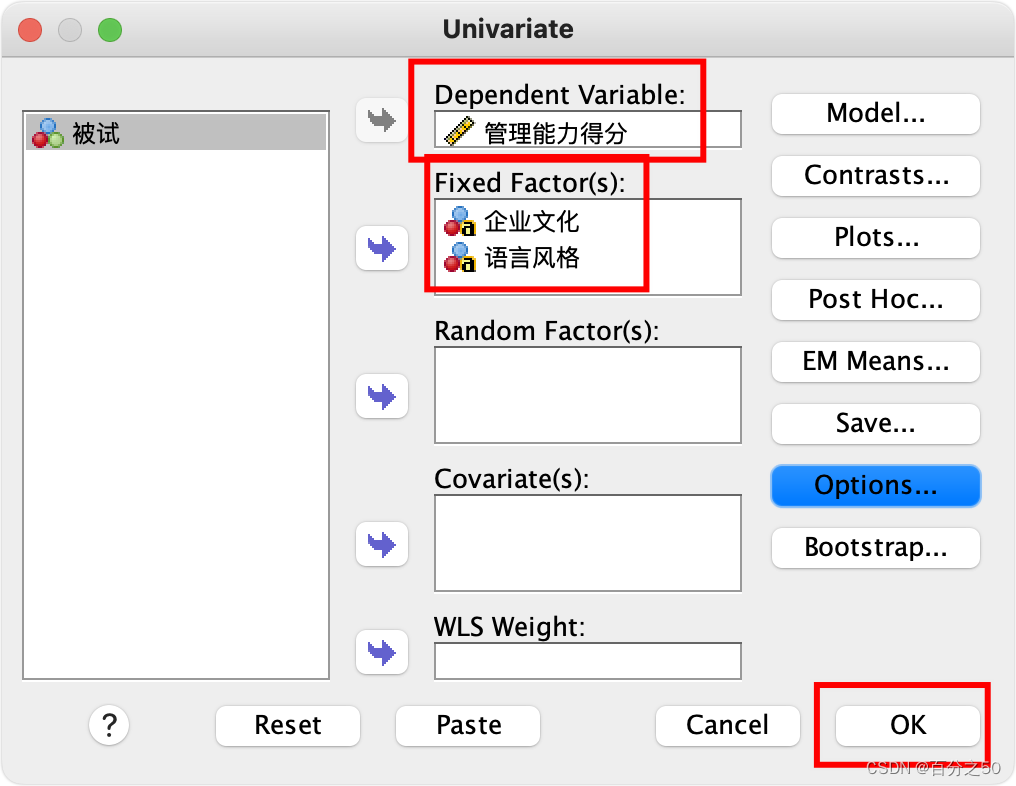
同样描述统计和齐性检验那些可以在选项里面选择,这里不选择,输出可以纯粹一点,结果见开头,不再重复贴出。
4.2 简单效应分析
4.2.1 Python代码
# 由于没有找到现成的方案,所以考虑对表格进行拆分,如果交互作用显著,
# 则读取表格中的某一变量的某个水平下的所有数据,然后进行t校验
# 这是自己写的一个简单的算法,如有更好的方法欢迎赐教
def simple_effect_analysis(check, melt_data):
dependent = "管理能力得分"
# 交互效应存在,进行简单效应分析,否则跳过
if check:
# 简单效应分析需要分别
# 检测企业文化为"个人努力"下的不同语言风格差异,
# 以及企业文化为"团队合作"下的不同语言风格差异,
# 分别对两种情况进行t检验即可
groups = melt_data.groupby(melt_data.企业文化)
for company_culture in ["个人努力", "团队合作"]:
melt_data = groups.get_group(company_culture)
# print(melt_data)
# 分别比较在不同企业文化下,不同语言风格对管理能力得分影响的差异
print("\n=======%s企业文化下不同语言风格t检验分析结果=========" % company_culture)
t_test(melt_data)
def t_test(melt_data):
melt_data = melt_data[['语言风格', '管理能力得分']]
# print("melt_data=\n", melt_data)
groups = melt_data.groupby(melt_data.语言风格)
a_group = groups.get_group("优柔寡断")
# print("a_group=\n", a_group)
b_group = groups.get_group("斩钉截铁")
# print("b_group=\n", b_group)
t_value, p_value = stats.ttest_ind(a=a_group['管理能力得分'], b=b_group['管理能力得分'])
# T = (样本均值 - 总体均值或另一样本均值) / (标准误差)
print(f"T值:{t_value:.3f}, p值:{p_value:.3f}")
simple_effect_analysis()函数中,有两步关键的数据拆分,详细说明如下,
"""
df_two_way=
企业文化 语言风格 管理能力得分
被试
1 个人努力 优柔寡断 3.1
2 个人努力 优柔寡断 3.0
3 个人努力 优柔寡断 3.2
4 个人努力 斩钉截铁 4.7
5 个人努力 斩钉截铁 4.6
6 个人努力 斩钉截铁 4.8
7 团队合作 优柔寡断 4.5
8 团队合作 优柔寡断 4.4
9 团队合作 优柔寡断 4.6
10 团队合作 斩钉截铁 3.5
11 团队合作 斩钉截铁 3.4
12 团队合作 斩钉截铁 3.6
"""
# 将该数据按企业文化分组,然后按照对应的值,拆分为两个df格式的数据
def split_data(df_two_way):
groups = df_two_way.groupby(df_two_way.企业文化)
person_df = groups.get_group("个人努力")
team_df = groups.get_group("团队合作")
print(person_df)
print(team_df)
# 即可得到
"""
企业文化 语言风格 管理能力得分
被试
1 个人努力 优柔寡断 3.1
2 个人努力 优柔寡断 3.0
3 个人努力 优柔寡断 3.2
4 个人努力 斩钉截铁 4.7
5 个人努力 斩钉截铁 4.6
6 个人努力 斩钉截铁 4.8
"""
# 以及
"""
企业文化 语言风格 管理能力得分
被试
7 团队合作 优柔寡断 4.5
8 团队合作 优柔寡断 4.4
9 团队合作 优柔寡断 4.6
10 团队合作 斩钉截铁 3.5
11 团队合作 斩钉截铁 3.4
12 团队合作 斩钉截铁 3.6
"""然后t_test也用了相同的方式处理。
4.2.2 SPSS中的简单效应分析
据我所知,SPSS中没有直接的点击操作可以进行简单效应分析,所以这部分要进入语法编辑器中进行操作。
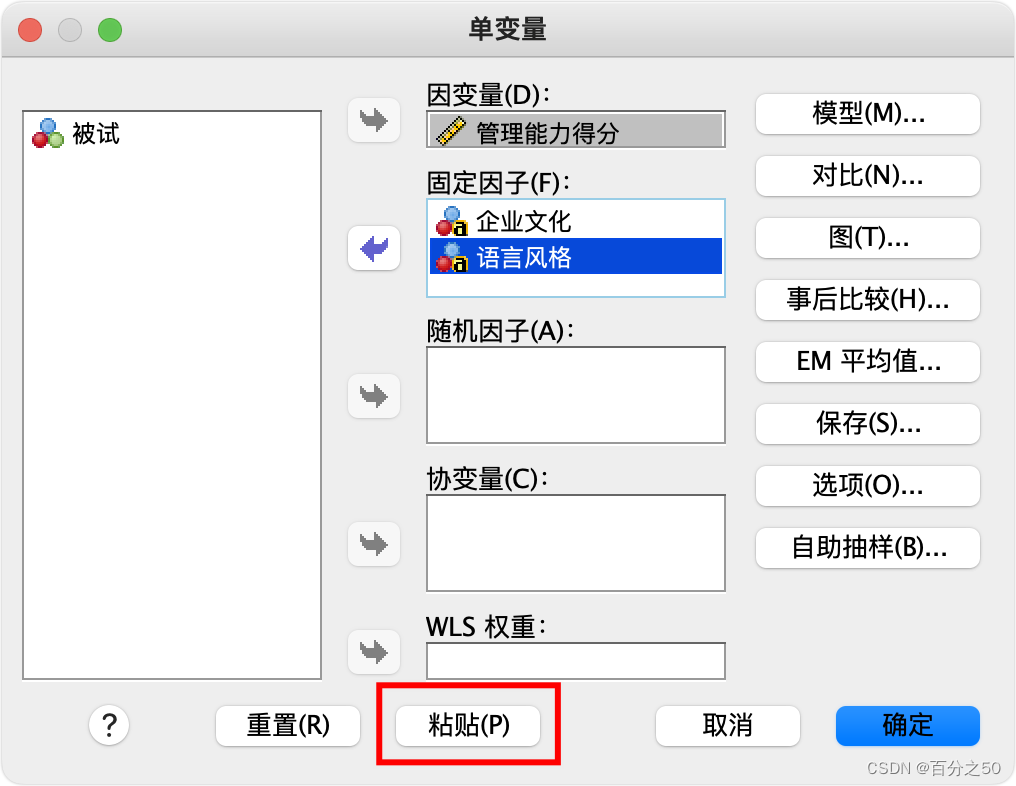
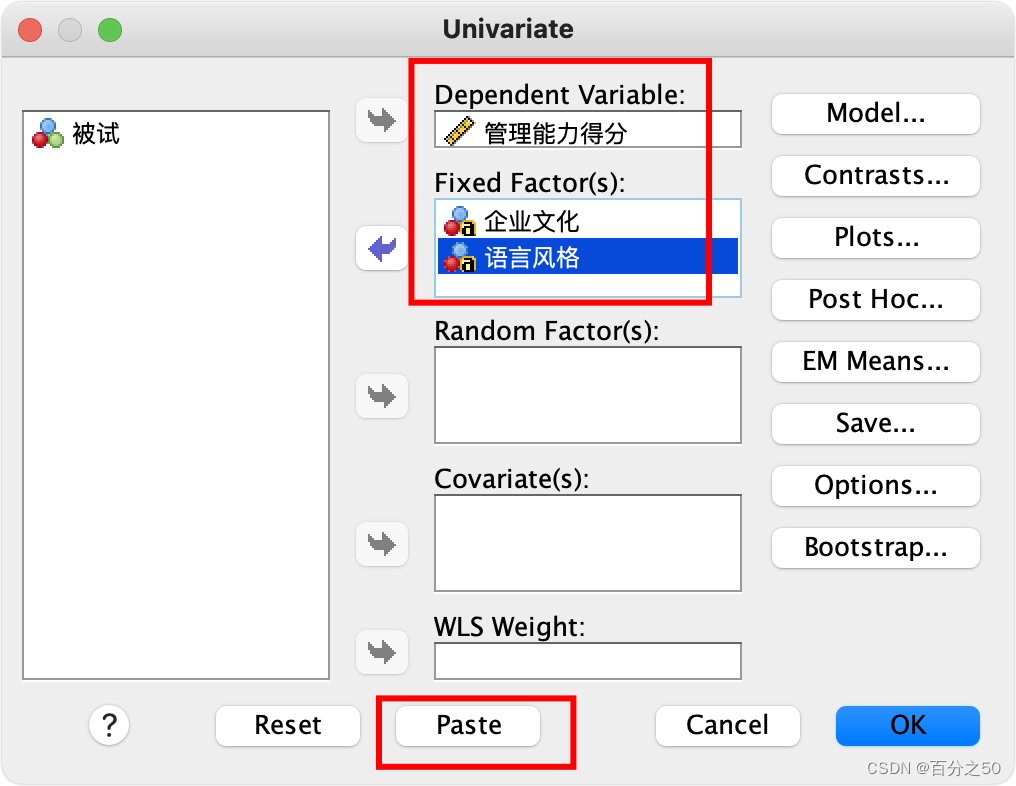
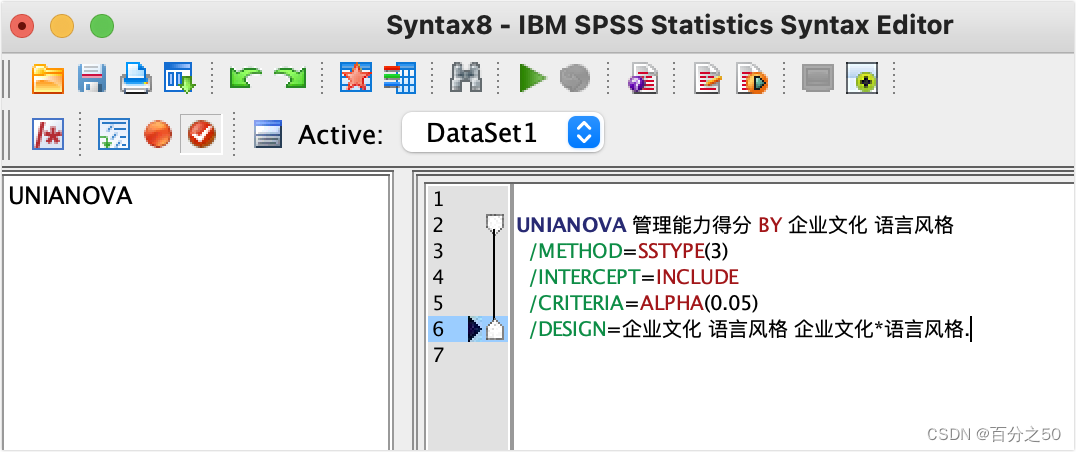
UNIANOVA 管理能力得分 BY 企业文化 语言风格:这部分表示要进行单因素方差分析(UNIANOVA),因变量是“管理能力得分”,自变量是“企业文化”和“语言风格”。/METHOD=SSTYPE(3):指定使用Type III SS(类型III平方和),这是计算F统计量所用的平方和类型。/INTERCEPT=INCLUDE:表示在模型中包含截距项。/CRITERIA=ALPHA(0.05):设置显著性水平为0.05。/DESIGN=企业文化 语言风格 企业文化*语言风格:指定用于设计的自变量,即“企业文化”、“语言风格”和它们的交互项“企业文化*语言风格”。
然后我们在中间加一句:/EMMEANS=TABLES(企业文化*语言风格) COMPARE(语言风格)ADJ(LSD)
DATASET ACTIVATE DataSet1.
UNIANOVA 管理能力得分 BY 企业文化 语言风格
? /METHOD=SSTYPE(3)
? /INTERCEPT=INCLUDE
? /EMMEANS=TABLES(企业文化*语言风格) COMPARE(语言风格)ADJ(LSD)
? /CRITERIA=ALPHA(0.05)
? /DESIGN=企业文化 语言风格 企业文化*语言风格.
/EMMEANS=TABLES(企业文化*语言风格) COMPARE(语言风格)ADJ(LSD):这部分是关于估计边际平均数(EMMEANS)的命令,用于生成交叉表,比较不同组之间的平均数,并使用LSD(最小显著差异)方法进行多重比较。
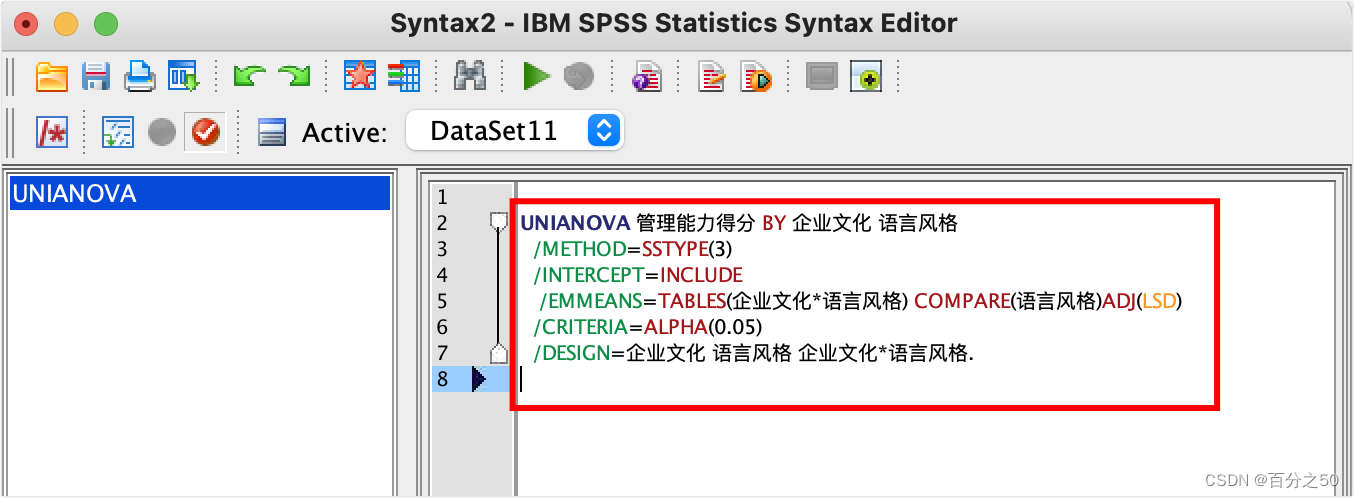
点击顶部的绿色三角即可运行,注意光标要放在代码块中。
输出结果如下:
中文版:
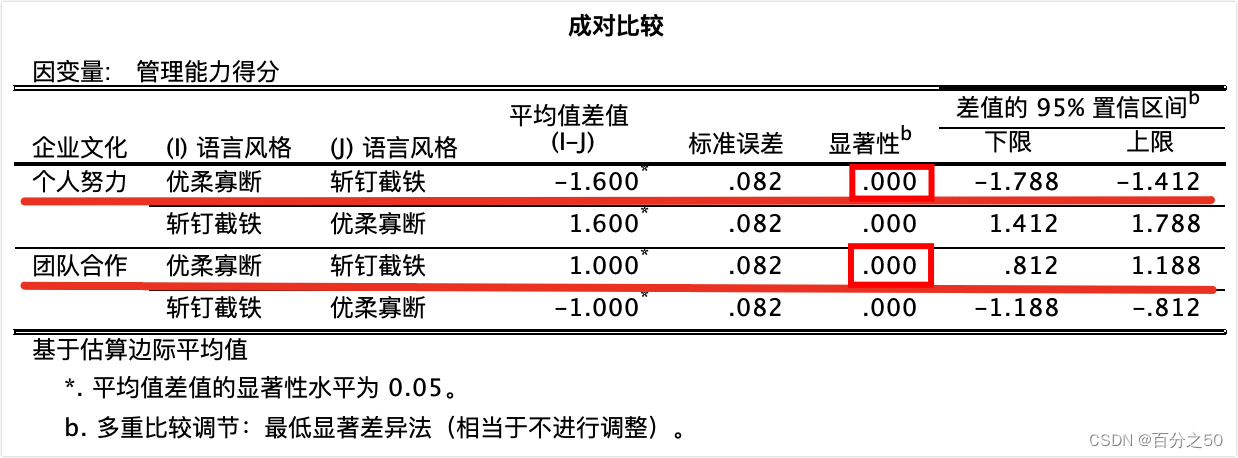
英文版:

END
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- ElasticSearch使用篇
- 供应链部门的OKR
- 1901. 寻找峰值 II --力扣 --JAVA
- 【PostgreSQL】从零开始:(三十二)数据类型-范围类型
- 半Happy的一天
- 【Mars3d】关于locationBar等控件的css样式冲突处理问题
- Spring Boot “How-to“ 指南中文文档-上
- UE5 - Polycam扫描文件导入插件
- 用minikube 搭建一个单机k8s玩玩
- FPGA高端项目:纯verilog的 25G-UDP 高速协议栈,提供工程源码和技术支持