【视觉SLAM十四讲学习笔记】第六讲——非线性最小二乘

专栏系列文章如下：
【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍
【视觉SLAM十四讲学习笔记】第二讲——初识SLAM
【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵
【视觉SLAM十四讲学习笔记】第三讲——旋转向量和欧拉角
【视觉SLAM十四讲学习笔记】第三讲——四元数
【视觉SLAM十四讲学习笔记】第三讲——Eigen库
【视觉SLAM十四讲学习笔记】第四讲——李群与李代数基础
【视觉SLAM十四讲学习笔记】第四讲——指数映射
【视觉SLAM十四讲学习笔记】第四讲——李代数求导与扰动模型
【视觉SLAM十四讲学习笔记】第五讲——相机模型
【视觉SLAM十四讲学习笔记】第六讲——状态估计问题

非线性最小二乘

先来考虑一个简单的最小二乘问题：

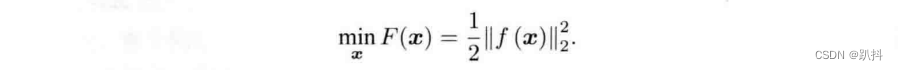
其中，自变量x∈Rⁿ ，f是任意标量非线性函数f(x) : Rⁿ → R。

下面讨论如何求解这样一个优化问题。显然，如果f是个数学形式上很简单的函数，那么该问题可以用解析形式来求。令目标函数的导数为零，然后求解x的最优值，就和求二元函数的极值一样：

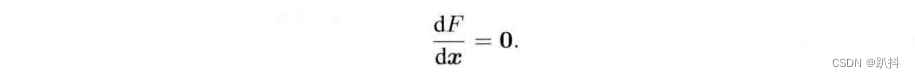
解此方程，就得到了导数为零处的极值。它们可能是极大、极小或鞍点处的值，只要逐个比较它们的函数值大小即可。但是，这个方程是否容易求解，取决于f导函数的形式。如果f为简单的线性函数，那么这个问题就是简单的线性最小二乘问题，但是有些导函数可能形式复杂，使得该方程可能不容易求解。求解这个方程需要我们知道关于目标函数的全局性质，而通常这是不大可能的。对于不方便直接求解的最小二乘问题，我们可以用迭代的方式，从一个初始值出发，不断地更新当前的优化变量，使目标函数下降。具体步骤如下：

这让求解导函数为零的问题变成了一个不断寻找下降增量Δx_k的问题。由于可以对f进行线性化，增量的计算将简单很多。当函数下降直到增量非常小的时候，就认为算法收敛，目标函数达到了一个极小值。在这个过程中，问题在于如何找到每次迭代点的增量，而这是一个局部的问题，我们只需要关心f在迭代值处的局部性质而非全局性质。

接下来，我们考察如何寻找这个增量Δx_k。

一阶和二阶梯度法

现在考虑第k次迭代，假设我们在x_k处，想要寻到增量Δx_k，那么最直观的方式是将目标函数在x_k附近进行泰勒展开：

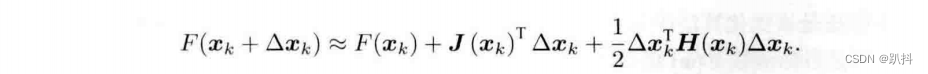
其中J(x_k)是F(x)关于x的一阶导数（也叫梯度、雅可比矩阵），我们把J(x)写成列向量，它可以和Δx进行内积，得到一个标量。H则是二阶导数（海塞矩阵），它们都在x_k处取值。我们可以选择保留泰勒展开的一阶或二阶项，那么对应的求解方法则成为一阶梯度或二阶梯度法。

最速下降法

如果保留一阶梯度，那么取增量为反向的梯度，即可保证函数下降：

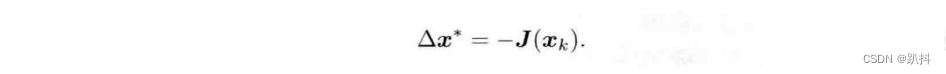
当然这只是个方向，通常我们还要再指定一个步长λ。步长可以根据一定的条件来计算，这种方法被称为最速下降法。它的直观意义很简单，只要我们沿着反向梯度方向前进，在一阶（线性）的近似下，目标函数必定会下降。

注意，以上讨论都是在第k次迭代时进行的，并不涉及其他的迭代信息。所以为了简化符号，我们省略下标k，并认为这些讨论对任意一次迭代都成立。

牛顿法

另外，我们可选择保留二阶梯度信息，此时增量方程为：

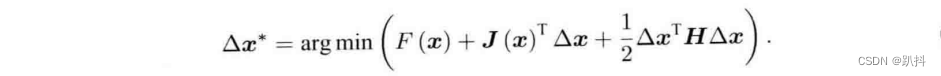
右侧只含Δx的零次、一次和二次项。求右侧等式关于Δx的导数并令它为零，得到：

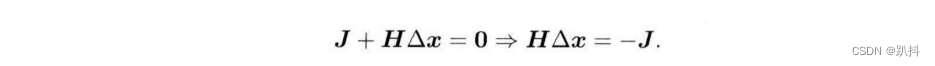
求解这个线性方程，就得到了增量。该方法又称为牛顿法。

我们看到，一阶和二阶梯度法都十分直观，只要把函数在迭代点附近进行泰勒展开，并针对更新量做最小化即可。事实上，我们用一个一次或二次的函数近似了原函数，然后用近似函数的最小值来猜测原函数的极小值。只要原目标函数局部看起来像一次或二次函数，这类算法就是成立的。

不过，这两种方法也存在它们自身的问题。最速下降法过于贪心，容易走出锯齿路线，反而增加了迭代次数。而牛顿法则需要计算目标函数的H矩阵，这在问题规模较大时非常困难，我们通常倾向于避免H的计算。对于一般的问题，一些拟牛顿法可以得到较好的结果，而对于最小二乘问题，还有更实用的方法：高斯牛顿法和列文伯格——马夸尔特方法。

高斯牛顿法

高斯牛顿法是最优化算法中最简单的方法之一。它的思想是将f(x)进行一阶的泰勒展开。请注意这里不是目标函数F(x)而是f(x)，否则就是牛顿法了。

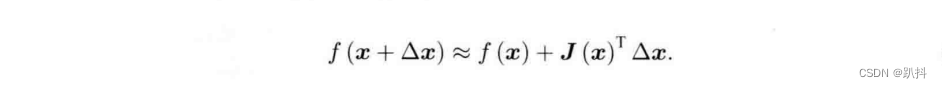
这里J(x)^T 为f(x)关于x的导数，为n × 1 的列向量。根据前面的框架，当前的目标是寻找增量Δx，使得||f(x+Δx)||² 达到最小。为了求Δx，我们需要解一个线性的最小二乘问题：

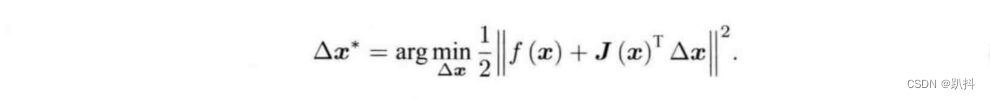
这个方程与之前有啥不一样呢？根据极值条件，将上述目标函数对Δx求导，并令导数为零。为此，先展开目标函数的平方项：

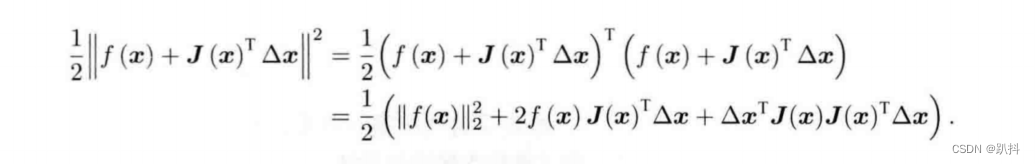
求上式关于Δx的导数，并令其为零：

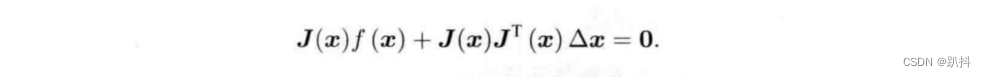
可以得到如下方程组：

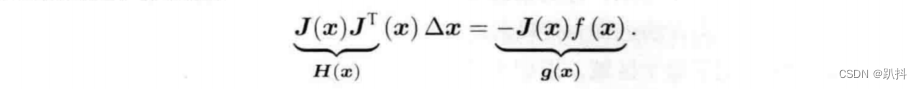
这个方程是关于变量Δx的线性方程组，我们称它为增量方程，也可以称为高斯牛顿方程或者正规方程。我们把左边的系数定义为H，右边定义为g，那么上式变为

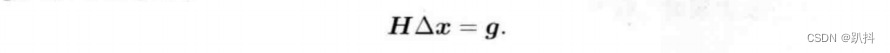
这里把左侧记作H是有意义的。对比牛顿法可见，高斯牛顿法用JJ^T 作为牛顿法中二阶海塞矩阵的近似，从而省略了计算H的过程。求解增量方程是整个优化问题的核心所在。如果我们能够顺利解出该方程，那么高斯牛顿法的算法步骤可以写成：

从算法步骤中可以看到，增量方程的求解占据着主要地位。只要我们能够顺利解出增量，就能保证目标函数能够正确地下降。

为了求解增量方程，我们需要求解H^-1，这需要H矩阵可逆，但实际数据中计算得到的JJ^T 却只有半正定性。也就是说，在使用高斯牛顿法时，可能出现JJ^T为奇异矩阵或者病态的情况，此时增量的稳定性较差，导致算法不收敛。直观地说，原函数在这个点的局部近似不像一个二次函数。更严重的是，就算我们假设H非奇异也非病态，如果我们求出来的步长Δx太大，也会导致我们采用的局部近似式不够准确：

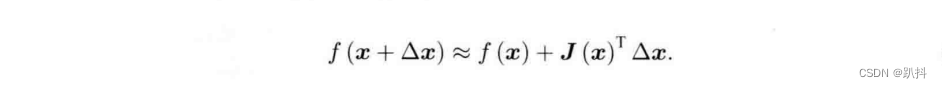
这样一来，我们甚至无法保证他的迭代收敛，哪怕是让目标函数变得更大都是有可能的。

尽管高斯牛顿法有这些缺点，但它依然算是非线性优化方面一种简单有效的方法。在非线性优化区域，相当多的算法都可以归结为高斯牛顿法的变种。这些算法都借助了高斯牛顿法的思想并且通过自己的改进修正其缺点。例如，一些线搜索方法加入了一个步长α，在确定了了Δx后进一步找到α使得||f(x+αΔx)||² 达到最小，而不是简单地令α=1。

列文伯格—马夸尔特方法

列文伯格—马夸尔特方法在一定程度上修正了高斯牛顿法的问题。一般认为它比后者更健壮，但是收敛速度可能比高斯牛顿法更慢，被称为阻尼牛顿法。

高斯牛顿法中采用的近似二阶泰勒展开只能在展开点附近有较好的近似效果，所以我们很自然地想到应该给Δx添加一个范围，称为信赖区域（Trust Region）。这个范围定义了在什么情况下二阶近似是有效的，这类方法也称为信赖区域方法（Trust Region Method）。在信赖区域里，我们认为近似是有效的；出了这个区域，近似可能会出问题。

那么，如何确定这个信赖区域的范围呢？一个比较好的方法是根据我们的近似模型跟实际函数之间的差异来确定：如果差异小，说明近似效果好，我们扩大近似的范围；反之，如果差异大，就缩小近似的范围。我们定义一个指标ρ来刻画近似的好坏程度：

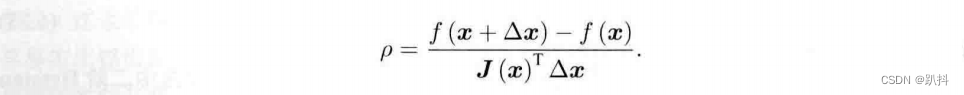
ρ的分子式实际函数下降的值，分母是近似模型下降的值。如果ρ接近于1，则近似是好的。如果ρ太小，说明实际减小的值远少于近似减小的值，则认为近似比较差，需要缩小近似范围。如果ρ比较大，则说明实际下降的比预计的更大，我们可以放大近似范围。

于是，我们构建一个改良版的非线性优化框架，该框架会比高斯牛顿法有更好的效果：

这里近似范围扩大的倍数和阈值都是经验值，可以替换成别的数值。在式(6.35)中，我们把增量限定于一个半径为μ的球中，认为只在这个球内才是有效的。带上D之后，这个球可以看成一个椭球。在列文伯格提出的优化方法中，把D取成单位阵I，相当于直接把Δx_k约束在一个球中。随后，马夸尔特提出将D取成非负数对角阵——实际中通常用J^TJ的对角元素平方根，使得在梯度小的维度上约束范围更大一些。

无论如何，在列文伯格—马夸尔特优化中，我们都需要解式(6.35)那样一个子问题来获得梯度。这个子问题是带不等式约束的优化问题，我们用拉格朗日乘子把约束项放到目标函数中，构成拉格朗日函数：

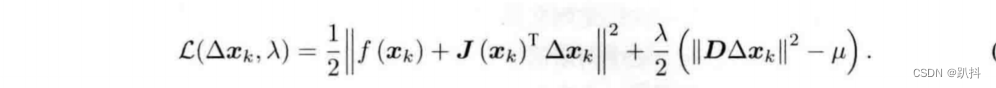
这里λ为拉格朗日乘子。类似于高斯牛顿法中的做法，令该拉格朗日函数关于Δx的导数为零，它的核心仍是计算增量的线性方程：

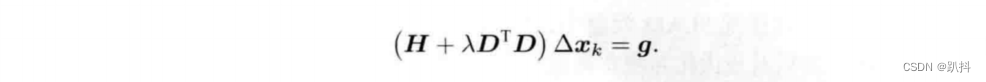
可以看到，相比于高斯牛顿法，增量方程多了一项λD^TD。如果考虑它的简化形式，即D=I，那么相当于求解：

我们看到，一方面，当参数λ比较小时，H占主要地位，这说明二次近似模型在该范围内是比较好的，列文伯格—马夸尔特方法更接近于高斯牛顿法。另一方面，当λ比较大时，λI占据主要地位，列文伯格——马夸尔特方法更接近于一阶梯度下降法（即最速下降），这说明附近的二次近似不够好。列文伯格—马夸尔特方法的求解方式，可在一定程度上避免线性方程组的系数矩阵的非奇异和病态问题，提供更稳定、更准确的增量Δx。

在实际问题中，我们通常选择高斯牛顿法或列文伯格—马夸尔特方法中的一种作为梯度下降策略。当问题性质较好时，用高斯牛顿。如果问题接近病态，则用列文伯格—马夸尔特方法。