【小白学机器学习4】从求f(x)的误差和函数E(θ)的导函数，到最速下降法，然后到随机梯度下降法

E(θ) 这个函数的可能形式

比如1元1次函数
f(x)=θ0+θ1*x
比如1元2次函数
f(x)=θ0+θ1*x+θ2*x^2
比如2元1次函数
f(x)=θ0+θ1*x1+θ2*x2+θ3*x3
更复杂点，比如n元n次函数（更通用的形式）
f(x)=θ10+θ11*x1+θ12*x1^2+θ13*x1^3+...
? ? ? ?θ20+θ21*x2+θ22*x2^2+θ23*x2^3+...
? ? ? ?....

1.4 调整参数θ0，θ1... ，试图找到f(x)的误差和函数E(θ)的最小值

评判函数就是E(θ) 这个关于误差和的函数。
当E(θ)取接近最小值的时候，就说明f(x) 对 y的拟合程度最好。
然后就不需要比较不同的 f(x) 之间的E(θ)差别了
而变成了比较通用的f(x) 里参数θ0，θ1... 等对f(x)的误差和函数E(θ)的影响，是否有最小值，是否可以找到最小值。

2 上述思路对应的操作上的步骤

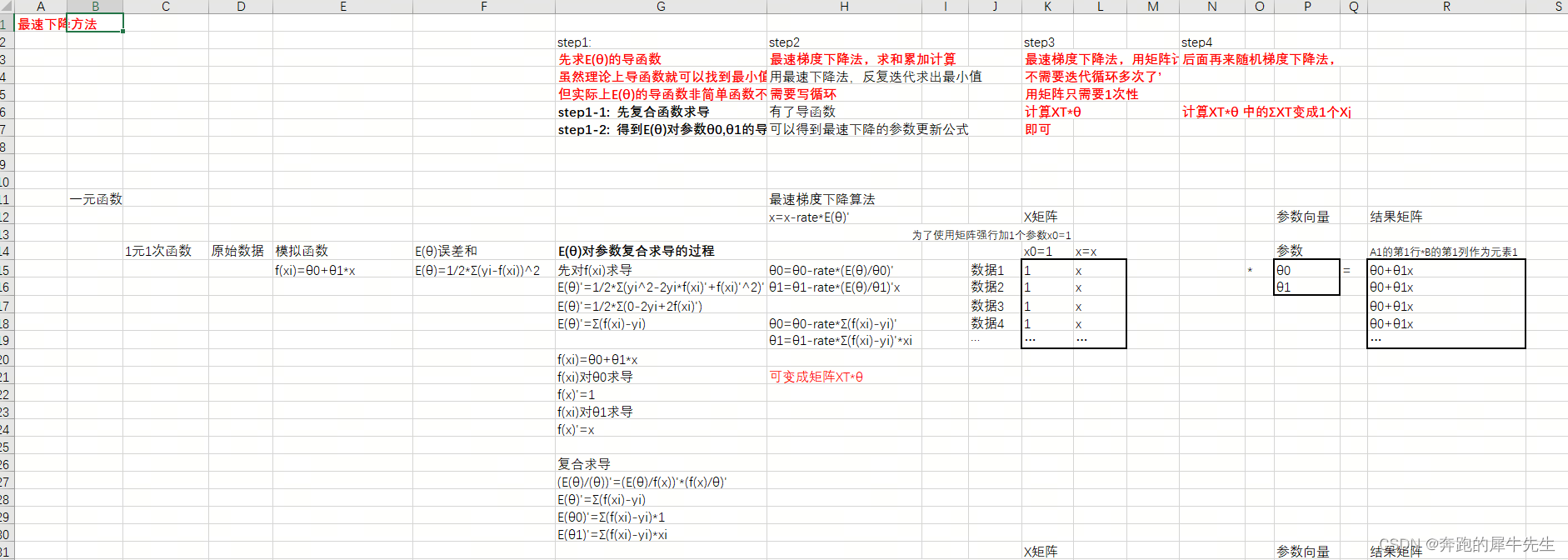
2.1 step1: ?先求E(θ)的导函数

虽然理论上导函数就可以找到最小值
但实际上E(θ)的导函数非简单函数不好求最小值
这里求E(θ)的导函数不是为了直接找导函数=0，从而找到函数E(θ)的最小值，从而找到模拟最好的f(x)曲线。
而是因为最速下降法的参数更新需要用到E(θ)的导函数。

x=x-rate*E(θ)'
step1-1: ?先E(θ)对每个参数θ复合函数求导
step1-2: ?得到E(θ)对参数θ0,θ1...的导函数

2.2 step2：最速梯度下降法，求和累加计算

有了导函数，就可以套用最速下降的参数更新公式
x=x-rate*E(θ)'
其中x 替换为参数θ0，θ1等
θ=θ-rate*E(θ)'
然后用最速下降法，反复迭代 θ=θ-rate*E(θ)' 求出收敛的最小值（如果有）
需要写迭代/循环，*Σ(f(xi)-yi) ，反复对参数进行更新

θ=θ-rate*E(θ)' 函数
θ0=θ0-rate*Σ(f(xi)-yi)'? ? ? ? ?'需要把所有数据?*Σ(f(xi)-yi) 进行求和
θ1=θ1-rate*Σ(f(xi)-yi)'*xi? ? ?'需要把所有数据?*Σ(f(xi)-yi) 进行求和
...

2.3 step3 ：最速梯度下降法，用矩阵计算

如果使用矩阵运算，用矩阵只需要1次性计算XT*θ即可
不需要迭代循环多次了

θ=θ-rate*E(θ)' 函数
θ0=θ0-rate*Σ(f(xi)-yi)'? ? =?θ0- rate*XT*θ? ? ? ? '一步计算即可
θ1=θ1-rate*Σ(f(xi)-yi)'*xi?=θ1- rate*XT*θ1? ? ?'一步计算即可
...

2.4 step4：用随机梯度下降法对最速下降法进行优化

再来随机梯度下降法，
计算XT*θ 中的ΣXT变成1个Xj
好处

减少了计算里，计算更快
避免了最速下降法的局部最优的问题

3 举例：1元1次函数

3.1 基础数据，x,y? 模拟函数f(x)，误差和函数E(θ)

先从最简单的一元函数开始，其中最简单的是1元1次函数

以1元1次函数为例：
原始数据 x,y
模拟函数 f(x)=θ0+θ1*x
误差和 E(θ)=1/2*Σ(yi-f(xi))^2

3.2?E(θ)对参数复合求导的过程

复合求导的方法
f(x/n)'=?f(x/m)' *f(m/n)'

先对f(xi)求导

E(θ)'=1/2*Σ(yi^2-2yi*f(xi)'+f(xi)'^2)'
E(θ)'=1/2*Σ(0-2yi+2f(xi)')
E(θ)'=Σ(f(xi)-yi)

f(xi)对θ0, θ1的求导

f(xi)=θ0+θ1*x
f(xi)对θ0求导,f(x)'=1
f(xi)对θ1求导,f(x)'=x

复合求导

(E(θ)/(θ))'=(E(θ)/f(x))'*(f(x)/θ)'
E(θ)'=Σ(f(xi)-yi)
E(θ0)'=Σ(f(xi)-yi)*1
E(θ1)'=Σ(f(xi)-yi)*xi

3.3?最速梯度下降算法

x=x-rate*E(θ)'
θ0=θ0-rate*(E(θ)/θ0)'
θ1=θ1-rate*(E(θ)/θ1)'x
θ0=θ0-rate*Σ(f(xi)-yi)'
θ1=θ1-rate*Σ(f(xi)-yi)'*xi
可变成矩阵XT*θ

?? ?X矩阵?? ?
?? ?为了使用矩阵强行加1个参数x0=1?? ?
?? ?x0=1?? ?x=x
数据1?? ?1?? ?x
数据2?? ?1?? ?x
数据3?? ?1?? ?x
数据4?? ?1?? ?x
…?? ?…?? ?…

参数向量?? ??? ?结果矩阵
?? ??? ?
参数?? ??? ?A1的第1行*B的第1列作为元素1
θ0?? ?=?? ?θ0+θ1x
θ1?? ??? ?θ0+θ1x
?? ??? ?θ0+θ1x
?? ??? ?θ0+θ1x
?? ??? ?…
?? ??? ?

3.4?随机梯度下降法，

后面再来随机梯度下降法，
计算XT*θ 中的ΣXT变成1个Xj

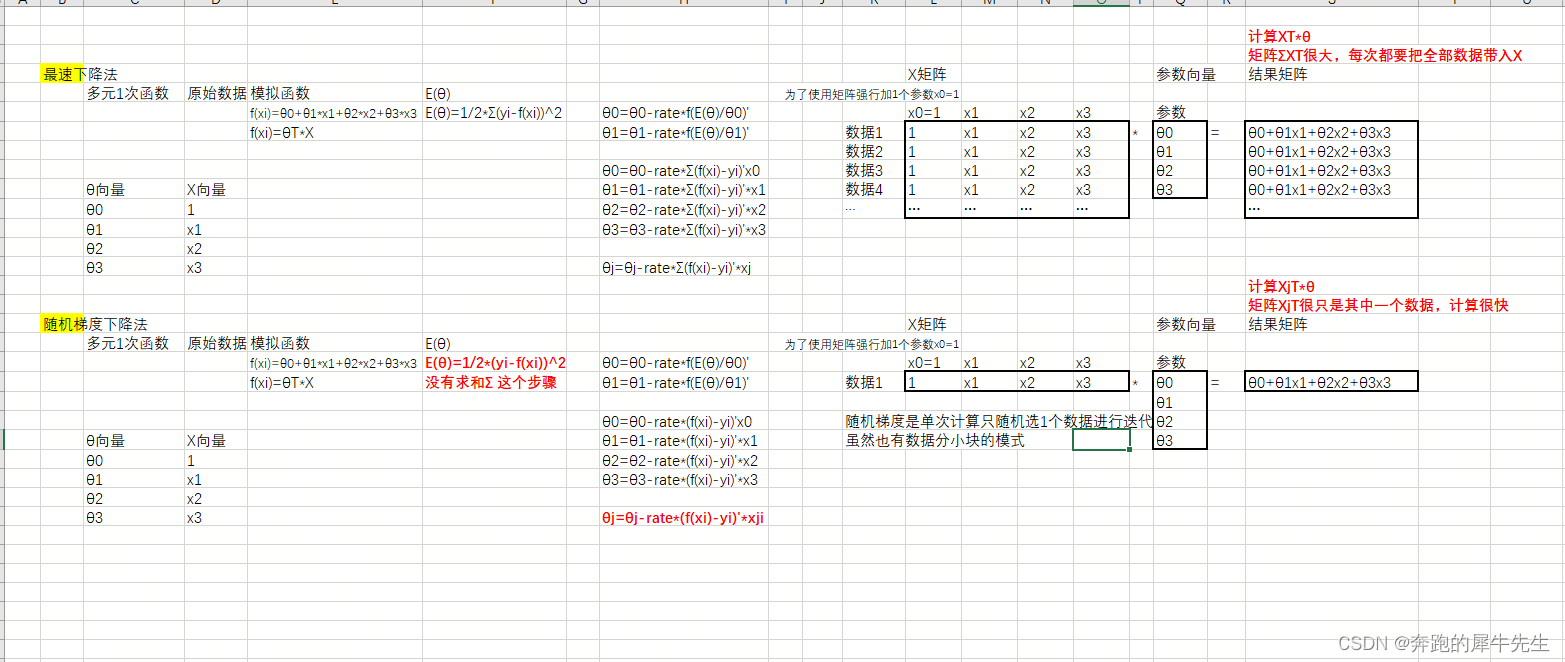
3.4.1 以多元1次函数为例子

模拟函数，多元1次函数，f(xi)=θ0+θ1*x1+θ2*x2+θ3*x3
其误差函数 E(θ)=1/2*Σ(yi-f(xi))^2

3.4.2 用最速下降法计算θ的迭代

θ0=θ0-rate*f(E(θ)/θ0)'
θ1=θ1-rate*f(E(θ)/θ1)'

求得导函数后展开为

θ0=θ0-rate*Σ(f(xi)-yi)'x0
θ1=θ1-rate*Σ(f(xi)-yi)'*x1
θ2=θ2-rate*Σ(f(xi)-yi)'*x2
θ3=θ3-rate*Σ(f(xi)-yi)'*x3

可以抽象为

θj=θj-rate*Σ(f(xi)-yi)'*xj
转化为矩阵计算？

3.4.3 随机梯度下降法

E(θ)
E(θ)=1/2*(yi-f(xi))^2

没有求和Σ 这个步骤

θ0=θ0-rate*f(E(θ)/θ0)'
θ1=θ1-rate*f(E(θ)/θ1)'