数据结构学习笔记(九)排序
1. 前言
这部分没有基于书上学习,基于知乎上一篇文章必学十大经典排序算法,看这篇就够了基础进行学习.关于GIF都是网上搜索的,如果侵权私我我直接删除.
图中所有算法都默认以从小到大的顺序排序。
2. 选择排序
选择排序,第一步选择数组中最小的元素和数组的第一个元素进行交换,第二步不管已经交换的第一个元素,从第二个元素开始的全新的数组找到最小的元素,和数组中的第一个元素进行交换。重复上步骤,直到将整个数组排序完。

实现
public class SelectSort{
public static int[] selectSort(int []a){
int n = a.length; // 获得数组长度
for(int i=0;i<n-1;i++){
int min = i; // 用于存储最小的数
for(int j = i+1;j<n;j++){ // 找到第i轮数组后最小的
if(a[min] > a[j]) min = j ;
}
int temp = a[i];
a[i] = a[j];
a[j] = temp; // 交换
}
}
3. 插入排序
插入排序就和抓扑克牌一样,不管没抓的那些,先抓一张牌,跟已经抓到手里的进行排序,并且插入到大于左边,小于右边的合适的位置。随后在抓一张牌。(抓了一张7,手里有排号的6和9,把这张7插入69之间,变成679,然后再抓下一张牌)

public class InsertSort{
public static int[] insertSort(int[] arr){
if(arr == null || arr.length <2) return arr;
int n = arr.length;
for(int i=1;i<n;i++){
int temp =arr[i];
int k = i-1; // k作为最后插入的位置的下标+1
while(k>=0 && arr[k] > temp){ // 比较已排序的牌,如果小于就往左边继续找
k--;
}
for(int j=i;i>k+1;j--)
arr[j] = arr[j-1]; // 腾位置
arr[k+1] = temp; // 插入
}
return arr;
}
}
4.冒泡排序
把第一个元素和第二个元素进行比较,如果第一个比第二个大,就交换位置,然后比较第二个元素和第三个元素,如果第三个元素大,就交换他们的位置。每一次循环,最后一个位置的元素一定是最大的,所以没开始一次循环,就少比较一次.
class BubbleSort{
public static int[] bubbleSort(int [] arr){
if(arr == null || arr.length <2){
return arr;
}
int n = arr.length;
for(int i = 0;i<n;i++){
for(int j = 0; j<n-1;j++){
if(arr[j+1] < arr[j]){
int temp = arr[j];
arr[j] = arr[i+1];
arr[j+1] = temp;
}
}
}
}
}
4.1 优化
如果从开始的第一对到结尾的最后一对,相邻之间的元素没有发生交换的操作,意味着右边的元素总大于左边的元素,此时数组已经是有序的,不需要对剩下的元素重复比较。
public class BubbleSort1{
public static int[] bubbleSort(int [] arr){
if(arr == null || arr.length <2){
return arr;
}
int n = arr.length;
for(int i = 0;i<n;i++){
boolean flag = true;
for(int j = 0; j<n-1;j++){
if(arr[j+1] < arr[j]){
int temp = arr[j];
arr[j] = arr[i+1];
arr[j+1] = temp;
}
}
if(flag = false)
break;
}
}
return arr;
}
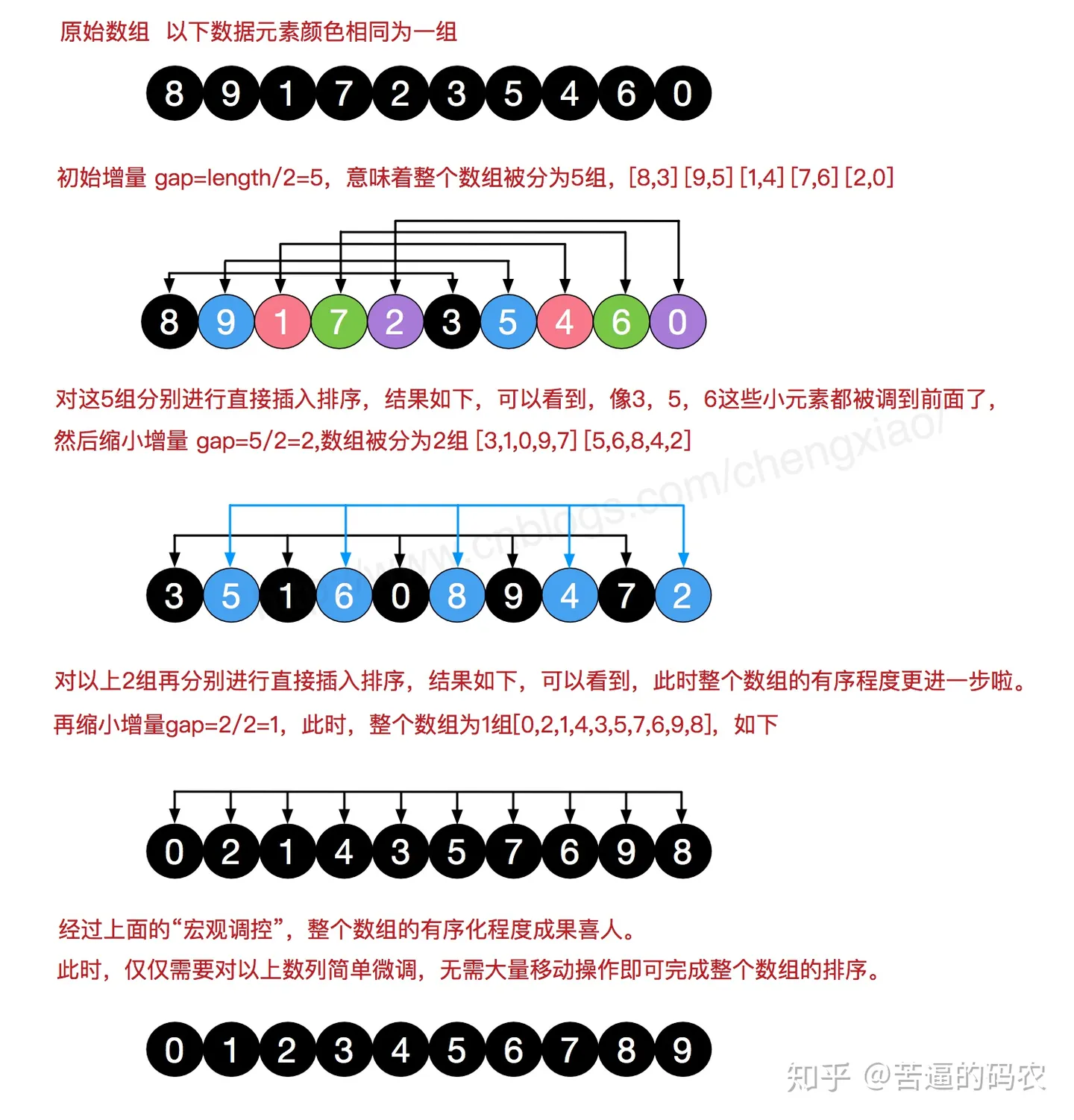
5.希尔排序
希尔排序是采用插入排序的方法,首先将元素按一定间隙分成几组,对每一组进行插入排序,然后把这几组分成间隙更小的几组,最后间隙变为1,就是只有一个组了,就排序完成了。
public class ShellSort{
public static int[] shellSort(int arr[]){
if(arr == null || arr.length <2) return arr;
int n = arr.length;
for(int h = n/2;h>0;h/=2){
// 分组
for(int i =h;i<n;i++){
InsertI(arr,h,i);
}
}
}
}
private static void InsertI(int[] arr,int h,int i){
int temp = arr[i];
int k;
for(k=i-h;k>0&& temp<arr[k];k-=h){ // 每一组的元素进行插入排序
arr[k+h] = arr[k];
}
arr[k+h] = temp;
}
6.归并排序
把大的数组分成两个数组,然后对两个数组进行分别排序,之后把两个数组合并成一个有序的数组,合并的时候是很快的。
通过递归的方式一直分割,直到数组的大小为1,此时只有一个元素,那么该数组就是有序的了,之后把两个数组大小为1的合并成一个大小为2的数组,再把两个数组大小为2的数组合成数组大小为4的数组,直到拼完整个数组。

递归:
public class MergeSort{
public sattic int[] mergeSort(int[] arr, int left, int right){
if(left < right){
int mid = (left+right)/2; // 分成两个数组
arr = mergeSort(arr, left, mid); // 对左半部分排序
arr = mergeSort(arr, mid+1, right); // 对右半部分排序
merge(arr,left,mid,right); // 合并
}
return arr;
}
private static void merge(int[] arr,int left, int mid, int right){
int[] a = new int[right - left +1]; // 用临时数组合并汇总
int i = left;
int j = mid +1;
int k =0;
while(i <= mid && j <= right){
if(arr[i] < arr[j]){
a[k++] = arr[i++];
}else{
a[k++] = arr[j++];
}
}
while(i <= mid) a[k++] = arr[i++];
while(j<=right) a[k++] = arr[j++];
for(i=0;i<k;i++){
arr[left++] = a[i];
}
}
}
非递归
public class MergeSort{
public static int[] mergeSort(int[] arr){
int n = arr.length;
for(int i = 1;i<n;i++){
int left = 0;
int mid = left +i-1;
int right = mid +i;
while(right<n){
merge(arr, left, mid ,right);
left = right +1;
mid = left+i-1;
right = mid +i;
}
if(left < n && mid <n){
merge(arr,left,mid ,n-1);
}
}
return arr;
}
}
7.快速排序
从数组中选择一个元素,把元素称为中轴元素,小于中轴元素的放左边,大于或等于中轴元素的放在右边,此时中轴元素所处的位置是最后的位置。
然后我们把中轴元素的左右两边分割为两个更小的数组(不包括中轴元素),让左右两边重复上面的操作,直到数组的大小为1.此时每个元素都是最终的位置。
步骤图解:
用双指针,一个指向数组头,一个指向数组尾。在用一个指针指向key,就是比较的标准,一般是数组的第一个元素。指向指针内数组元素是空,就说明有空位置给j那边的元素放,所以我们这时候把j往左边指就行,如果j指向的指针内数组元素是空,说明有空位置给i那边的元素放,这时候把i那边的指针往右边指。如果i = j了,我们就把最开始存的key 放进去,就能确定位置。
用一个简单的例子

- 用key 存储 num[0] ,此时i指向的空间为num[0],他应该没有存储数据。j指向num[n]。
key =45,作为比较的标准
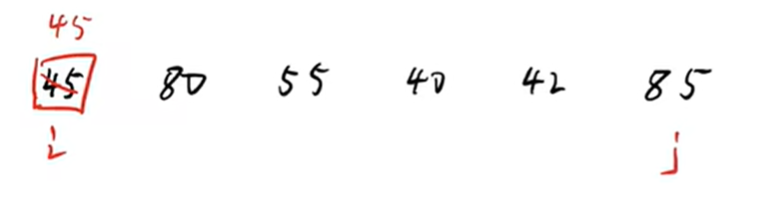
2) 看上面的介绍,因为i留了个新的空间出来,所以从j那边找存储的数据,
j -> 85 ,大于45,往左边继续找
j->42,小于45,把42存在空房间i指向的空间,并且把j指向的42的房间置位空
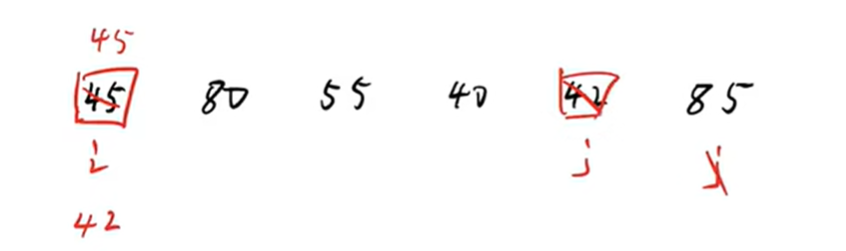
3) j指向的房间有空房间了,所以我们从i这边找
把i往右指
i->80,大于45,所以放在j指向的空房间

4)这时i指向80的房间空出来了,所以往j这边找,
j->40,小于45,所以往i这边的空房间放
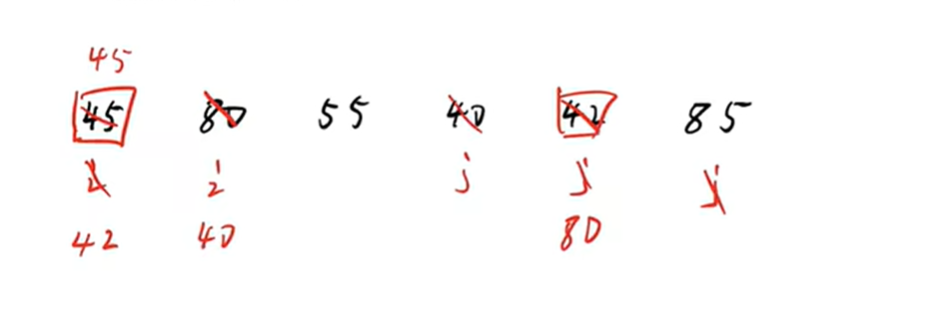
5) 这时候j这边空了个空房间出来,就往i这边找,
i->55 ,大于45,所以放在空房间

6) 这时候i存55的地方右空房间了,在j这边找
j->55 = i->55;
所以这个地方就是存一开始key的地方。
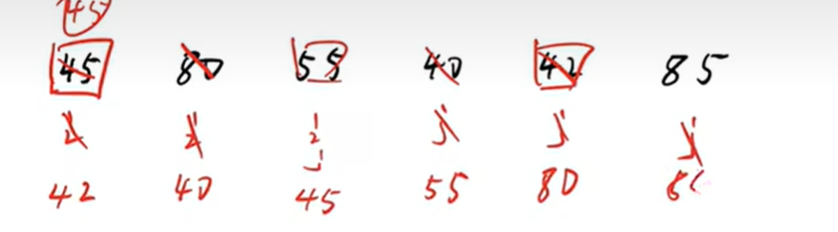
7) 第一趟就找完了,这时候因为找到了key的位置,把key左右两边分成两个新数组各自进行新一轮的排序。

数组为 【42, 40】 和【55,80,85】 进行排序
重复1-6的步骤,直到所有数组的元素为1就结束排序
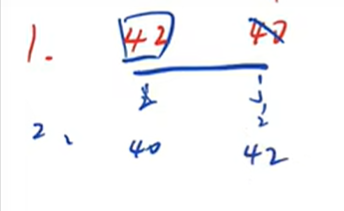
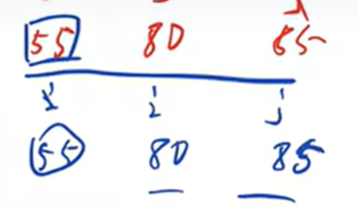
第二趟走完
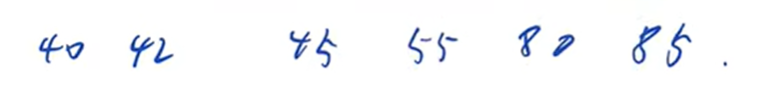
排序完成
public class QuickSort{
public static int[] quickSort(int[] arr,int left,int right){
if(left < right){
int mid = partition(arr,left,right);
arr = quickSort(arr, left, mid - 1);
arr = quickSort(arr, mid+1,right);
}
return arr;
}
private static int partition(int[] arr, int left, int right){
int pivot = arr[left];
int i = left + 1;
int j = right;
while(true){
while(i<=j && arr[i] <= pivot) i++; // 往右找第一个小于pivot的位置
while(i<=j && arr[j] >= pivot) j--; // 往左找第一个大于pivot的位置
if(i>j)
break;
int temp = arr[i]; // 交换位置
arr[i] = arr[j];
arr[j] = temp;
}
arr[left] = arr[j];
arr[j] = pivot;
return j; // 返回中轴元素位置
}
}
8.堆排序
这部分在堆中有体现,主要是插入一个新元素后堆不满足最小堆和最大堆,此时会进行上浮或下沉操作。
可以直接回去看堆相关内容
数据结构学习笔记(五)树
void MinHeap::siftUp(int start)
{
// 从结点start开始到结点0为止,自下向上进行比较,
// 如果子女的值小于父结点的值,则进行交换
int j = start; // 开始的地方
int i = (j - 1) / 2; // 开始的结点的父结点
int temp = heap[j]; // 暂时存放开始的结点
while (j > 0) {
if (heap[i] < temp) break; // 父结点值小,不调整
else {
heap[j] = heap[i]; // 父结点值大,交换
j = i;
i = (i - 1) / 2;
}
}
heap[j] = temp;
}
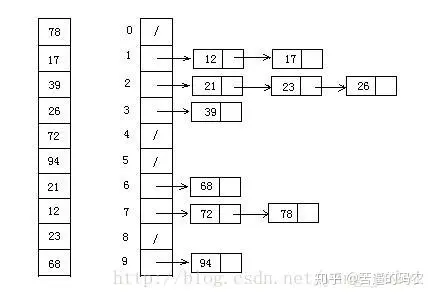
9.桶排序
把最大值和最小值之间进行瓜分,比如分成10个区间,10个区间对应10个桶,把各元素放在对应的桶中去。在对桶中的数据进行排序,之后每个桶中的数据都是有序的了,再合并起来。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 网络世界的黑暗角落:常见漏洞攻防大揭秘
- 通过myBatis将sql语句返回的值自动包装成一个java对象(2)
- 【算法分析】FlashAttention算法实例演示
- 了解一下InternLM2
- Android Studio中配置Flutter插件,创建小项目“hello world”
- 【电源专题】案例:不同的充电芯片在没插入电池但插入USB充电器情况下为什么无法兼容?
- 安达发|APS计划与排程软件之超级BOM功能
- 双十一邮件群发最佳时间:提升营销效果与转化率的关键节点
- 微信小程序列表点击Item回调
- 科研绘图(三)百分比堆叠线条图