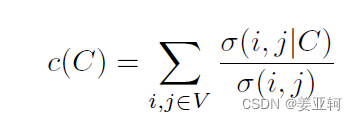中心性算法归纳

中心性算法不仅是在我所学习的计算机网络当中起很重要的作用，在交通网络、社交网络、信息网络、神经网络当中也有很多的应用例子。今天我在这里总结一下场景的几种中心性算法。

参考文献

Python NetworkX库

偏心中心性（Eccentricity Centrality）

偏心中心性是一种用于衡量网络中节点重要性的图论指标。这种中心性度量基于每个节点到网络中所有其他节点的最短路径的最大值。具体而言，一个节点的偏心中心性是由其到达网络中所有其他节点的最短路径中最长的那一个决定的。

下图中计算节点s的偏心中心性时，最远节点为t且距离为3，那么s的偏心中心性就是1/3

接近中心性（Closeness Centrality）

这是一个节点到网络中所有其他节点的平均最短路径长度的倒数。直观地说，接近中心性高的节点可以快速到达网络中的其他节点。这个指标在需要快速传播信息的网络中非常有用。

上图中计算节点s的中心性时，就计算它到所有节点的距离之和，再取倒数就行，标准化的话还需要再乘以节点数N-1

以上两种中心性算法的缺陷

如果在有向图中，两个节点的最短距离为无限大，也就是没有路径到达，那么中心性为0，就无法比较，所以以上两种中心性算法只能应用在强连通有向图当中。无向图当中，如果存在孤立点，也就是没有任何连接的节点，也无法应用以上两种中心性算法。

---

度中心性（Degree Centrality）

这是最直观的中心性定义，即一个节点的度（与其相连的边的数量）。在有向图中，我们可以进一步区分入度中心性（指向节点的边的数量）和出度中心性（从节点出发的边的数量）。度中心性是网络分析中最常用的中心性指标之一。

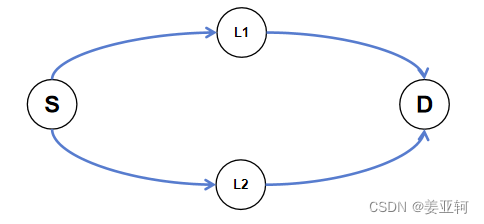
比如下面有向图当中，S的出度中心性为2，入度中心性为0

特征向量中心性（Eigenvector Centrality）

这是一个节点的重要性不仅取决于它有多少邻居，而且还取决于它的邻居是多么的重要。换句话说，如果一个节点与多个重要的节点相连，那么这个节点也被认为是重要的。这个指标在识别影响力大的节点方面非常有用，例如在社交网络分析中。

特征向量中心性需要计算邻接矩阵的特征值和对应的特征向量等，计算较为复杂，参照NetworkX库。

注意：在应用到有向图时，最大连通子图以外的节点中心性为0，而且最大特征值和特征向量可能不唯一，所以推荐将特征向量中心性应用到强连通无向图。

---

介数中心性（Betweenness Centrality）

这是一个节点在网络中所有节点对之间的所有最短路径中出现的次数。直观地说，介数中心性高的节点在网络中的信息流动中起着重要的作用。

介数中心性基于这样的假设：网络中的某些节点对于不同节点间的信息流动或互动起到关键的桥梁作用。它不仅仅考虑了一个节点的直接连接数量（如度中心性所做的那样），而是考虑了节点在连接网络中不同部分的能力。因此，即使一个节点的直接连接数不多，但如果它位于网络的关键位置（如连接两个大社交群体的桥梁），那么它的介数中心性也可能很高。

介数中心性在多种场景下非常有用，特别是在理解网络中信息流动、资源分配以及社交影响力方面。它帮助识别那些可能不是最明显的重要节点，但对于网络的整体结构和功能却至关重要的节点。

我们也可以通过下面的公式来理解，我们假设c(v) 代表节点 v 的介数中心性，σ(i, j)表示节点 i 和 j （i，j∈所有节点V）之间所有最短路径的集合，σ(i, j|v) 表示所有通过节点 v 的最短路径的总和。这样我们就能知道节点v的重要性。

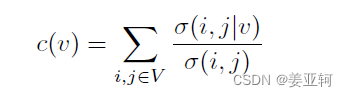
以下是两种由介数中心性衍生出来的中心性算法

最短路径中心性（Shortest Path Centrality）

这是一个节点在网络中所有节点对之间的所有最短路径中出现的次数。这与介数中心性非常相似，但通常用于加权网络，其中边的权重表示节点之间的距离或成本。

在NetworkX库当中，我们可以用betweenness_centrality算法当中的weight参数去定义每条边的权重，不然的话所有路径都是相同的权重。

组介数中心性（Group Betweenness Centrality）

这是一组节点在网络中所有节点对之间的所有最短路径中出现的次数。这个指标用于识别一组节点在网络中的整体重要性。

假设计算一组节点C的组介数中心性 c（C）组介数中心性，其中 σ(i, j) 代表节点 i 和 j（i，j∈所有节点V） 之间所有最短路径对的集合。σ(i, j|C) 代表的是所有通过群组 C 中任何节点的最短路径对的分数之和。计算之前，我们先要定义这组节点C的数目。

---

网页排名算法（PageRank）

PageRank是一种用于网页排名的算法，可以看作是特征向量中心性的一种变体，适用于有向图，特别是网页链接网络。PageRank 的核心思想基于这样一个假设：重要的网页很可能被其他重要网页所链接。

这个算法基于两个关键原则：

• 链接数量：如果一个网页被许多其他网页链接（引用），那么这个网页被认为是重要的，因此应该有一个较高的PageRank值。
• 链接质量：如果一个网页被已经被认为重要（即具有高PageRank值）的网页所链接，那么这个链接对该网页的PageRank值的贡献会更大。