关于大模型学习中遇到的2

来源：网络

一小时实践入门 PyTorch

简介

PyTorch 是一个开源的深度学习库，由 Facebook 的人工智能研究团队开发和维护。PyTorch 提供了两个主要的功能：

1. 多维张量的操作：PyTorch 提供了一个类似于 NumPy 的库，用于对多维数组（也称为张量）进行操作。与 NumPy 不同，PyTorch 的张量可以在 GPU 上运行，这使得其可以进行更快的数学运算。
2. 深度学习：PyTorch 提供了一套全面的深度学习函数和类，支持各种类型的神经网络。PyTorch 的一个关键特性是动态计算图，这使得用户可以动态地更改神经网络的结构，这在某些复杂的模型中是非常有用的，如递归神经网络。

PyTorch 有一个活跃的社区，提供了大量的预训练模型、学习资源和工具库。此外，PyTorch 的接口设计得简洁直观，因此它对于初学者来说是非常友好的。

PyTorch 还支持分布式训练，使其可以在多个 GPU 或多个服务器上进行训练。其易用性、灵活性以及强大的功能使得 PyTorch 已经成为了学术界和工业界的首选深度学习库之一。

前置知识

在开始学习 PyTorch 之前，确实有一些基本的技术和软件知识是你需要了解的：

1. Python：PyTorch 是一个 Python 库，所以你需要对 Python 语言有一定的了解。这包括基本的语法、数据类型（如列表、字典和元组）以及函数和类的使用。更高级的 Python 知识，如生成器和装饰器，虽然不是必需的，但是在某些情况下可能会有所帮助。
2. NumPy：NumPy 是 Python 的一个重要的科学计算库，它提供了多维数组对象以及大量的函数来操作这些数组。PyTorch 的 Tensor 对象在很大程度上是受 NumPy 的影响，所以对 NumPy 的了解会对学习 PyTorch 有所帮助。
3. 基本的线性代数、微积分和概率论：PyTorch 是一个用于深度学习的库，而深度学习是建立在这些数学概念上的。你不需要成为这些主题的专家，但是至少要理解向量、矩阵、微分、概率等基本概念。
4. 深度学习基础：虽然你可以在学习 PyTorch 的过程中学习深度学习的概念，但是对神经网络的基本理解会有所帮助。这包括了解神经网络的结构（如层、神经元、激活函数）以及训练过程（如前向传播、反向传播、损失函数和优化器）。
5. Jupyter Notebook：Jupyter Notebook 是一种网页应用，允许你创建和共享包含实时代码、方程、可视化和描述性文本的文档。它是机器学习和数据科学领域的常用工具，也经常用于展示和共享 PyTorch 代码。
6. 使用 GPU：如果你计划使用 GPU 来加速你的 PyTorch 代码，你可能需要了解一些基本的 CUDA 知识。CUDA 是由 NVIDIA 开发的一种用于通用并行计算的技术，它允许开发者利用 NVIDIA 的 GPU 来执行非图形计算任务。

这些只是开始学习 PyTorch 的一些基本知识，随着你的学习深入，你可能还需要了解更多的概念和技术，例如卷积神经网络（CNN）、循环神经网络（RNN）、迁移学习等。

学习计划

从你的已有知识来看，你已经具备了 Python 基础和一些 Python 数据科学库的使用经验（如 numpy 和 pandas）。这为你快速学习 PyTorch 打下了很好的基础。

接下来，我为你规划一个一小时学习 PyTorch 的计划。这个计划的目标是让你了解 PyTorch 的基本概念，如 Tensor、自动梯度（autograd）以及如何构建和训练一个简单的神经网络。具体如下：

了解 PyTorch 的基本概念 (15 分钟)：

• • 张量（Tensor）：PyTorch 的基本构建块。你可以把它看作是一个多维数组。
  • 自动梯度（Autograd）：PyTorch 的一个关键特性，它能够自动地计算梯度，这对于神经网络的训练非常重要。

手动实践（30 分钟）：

• • 创建和操作张量：尝试创建你自己的张量，并进行一些基本操作，如加法、乘法等。
  • 理解自动梯度：创建一些张量，然后尝试使用 PyTorch 的 autograd 功能来计算它们的梯度。

构建和训练一个简单的神经网络（15 分钟）：

• • 使用 PyTorch 构建一个简单的全连接神经网络（也称为多层感知器）。
  • 使用一个简单的数据集（比如 MNIST 手写数字识别数据集）来训练你的神经网络。

你可以参考 PyTorch 的官方文档或者查找一些在线教程来进行学习。PyTorch 的官方网站提供了一些非常好的教程，适合初学者。

请注意，深度学习是一个复杂的领域，一小时只能让你了解到皮毛。如果你想要深入学习 PyTorch 和深度学习，你可能需要投入更多的时间，并学习更多的理论知识。

PyTorch的安装

官网下载安装

要在 Windows 系统中安装 PyTorch，你首先需要安装 Python 和 pip（Python 的包管理器）。从 Python 官方网站下载并安装 Python 后，pip 通常会被一起安装。你可以通过在命令行中运行?python --version?和?pip --version?来检查它们是否已经安装。

要选择正确的 PyTorch 版本来下载，你可以按照以下步骤操作：

打开 PyTorch 的官方网站：https://pytorch.org

在主页上找到并点击 "Get Started" 按钮，或者直接进入：https://pytorch.org/get-started/locally/

在这个页面，你可以看到一个名为 "Quick Start Locally" 的表格。在这个表格中，你可以选择你的设置，然后网站会为你生成对应的安装命令。

• • "PyTorch Build"：选择你想要的 PyTorch 版本，一般选择 "Stable" 表示稳定版本。
  • "Your OS"：选择你的操作系统，例如 "Windows"。
  • "Package"：选择你想使用的包管理器。如果你在使用 Python，你应该选择 "Pip"。
  • "Language"：选择你打算用来编写 PyTorch 代码的编程语言，这里选择 "Python"。
  • "CUDA"：选择你的 CUDA 版本。如果你的计算机没有 NVIDIA 的 GPU，或者你没有安装 CUDA，那么选择 "None"。否则，选择你的 CUDA 版本，例如 "10.2"。

在你填完所有的设置后，网站会在表格下方生成一个安装命令。你可以复制这个命令，然后在你的命令行中运行它来安装 PyTorch。

这就是如何在 PyTorch 官网选择下载对应版本的 PyTorch 的方法。

cpu版本安装后怎么改成gpu版本

不需要卸载当前的 PyTorch 版本，只需要按照 GPU 版本的安装命令重新安装一次就可以了。重新安装的过程会自动覆盖原有的 PyTorch 版本。请确保你的 CUDA 版本和 PyTorch 支持的 CUDA 版本一致。

在 PyTorch 官网的获取安装命令的页面，选择合适的 PyTorch 版本、操作系统、包管理器（pip 或 conda）、Python 版本，以及你的 CUDA 版本，然后运行生成的命令。

例如，如果你正在使用 pip 和 CUDA 10.2，那么你可以运行以下命令：

pip install torch==1.8.1+cu102 torchvision==0.9.1+cu102 torchaudio===0.8.1 -f https://download.pytorch.org/whl/torch_stable.html

这个命令会下载并安装支持 CUDA 10.2 的 PyTorch 1.8.1 版本。

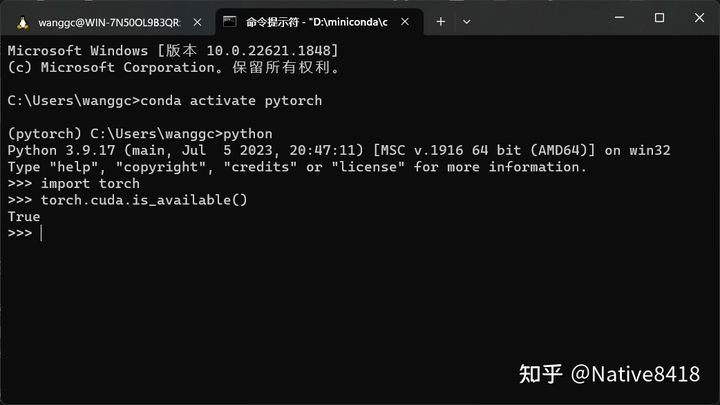
安装完成后，你可以使用以下 Python 代码来验证 PyTorch 是否能够使用 GPU：

import torch

# 如果下面的命令返回 True，则表示 PyTorch 能够使用 GPU
torch.cuda.is_available()

如果你的系统中安装了多个 CUDA 版本，或者你不确定你的 CUDA 版本，你可以使用?nvcc --version?命令来查看。

gpu版本的pytorch的安装需要安装 cuda 和 cudnn，需要和自己的显卡版本匹配。我很早之前安装过了，这里省略。对于这篇文章来说不涉及GPU的内容，CPU版就够了。

PyTorch 的基本概念?

张量

张量（Tensor）是 PyTorch 中的核心概念，它类似于 Python 的 Numpy 中的 ndarray 对象，但是提供了更强大的功能，比如 GPU 计算的支持以及自动求导。在 PyTorch 中，所有的操作，包括数学运算，神经网络的输入、输出，以及模型的参数，都是通过张量来进行的。

张量可以在 CPU 或 GPU 上创建和操作，可以进行各种算术操作。张量的维度可以是任意的。例如，你可以有一个 0 维的张量（也就是一个标量），1 维的张量（也就是一个向量），2 维的张量（也就是一个矩阵），或者更高维度的张量。

PyTorch 张量的一些主要特性包括：

• 数据类型: PyTorch 张量可以是不同的数据类型，如整型、浮点型和复数型等。
• 设备兼容性: 张量可以在 CPU 或 GPU 上创建和操作，这使得 PyTorch 可以利用 GPU 进行快速计算。
• 与 Numpy 兼容性: PyTorch 张量可以和 Numpy 数组互相转换，这使得你可以利用 Numpy 的强大功能进行数据处理。
• 自动求导: 张量可以跟踪计算历史并自动计算梯度，这是训练神经网络的关键。

在 PyTorch 中，你可以使用各种方式创建张量，例如，你可以直接从数据创建，也可以使用一些函数来创建特定形状的张量，如全 0 的张量，全 1 的张量，随机张量等。

例如，你可以这样创建一个张量：

import torch

# 创建一个 2x3 的零张量
x = torch.zeros(2, 3)
print(x)

# 创建一个 2x3 的随机张量
y = torch.rand(2, 3)
print(y)

# 创建一个从数据中的张量
z = torch.tensor([1.0, 2.0, 3.0])
print(z)

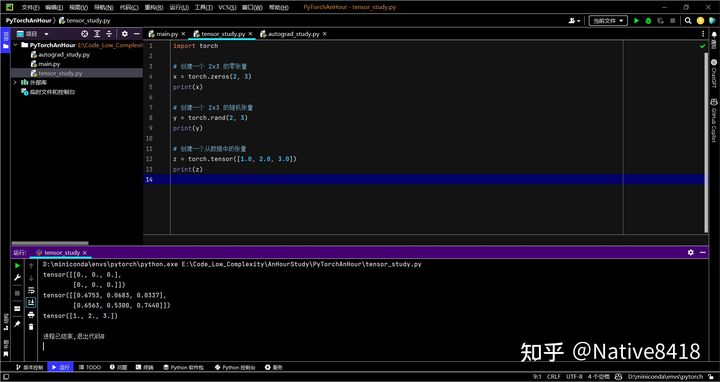
以上就是 PyTorch 中的张量的基本介绍。在深度学习中，理解和掌握张量的操作是非常重要的。

自动梯度

PyTorch 的自动梯度（Autograd）系统是 PyTorch 所有神经网络的核心。Autograd 自动处理所有计算的梯度。这是一个运行时定义的框架，意味着反向传播是根据你的代码如何运行来定义的，每次迭代都可能不同。

PyTorch 中的?torch.Tensor?类是这个 autograd 系统的核心。如果你设置了它的属性?.requires_grad?为?True，它就会开始追踪在其上的所有操作。完成计算后，你可以调用?.backward()?来自动计算所有的梯度。这个张量的梯度将会累积到?.grad?属性中。

如果你不想让一个张量被进一步的追踪，你可以调用?.detach()?方法来将其从追踪记录中分离出来，这样它以后的操作就不会被追踪了。为了防止跟踪历史（和使用内存），你还可以使用?torch.no_grad()?包装代码块，这在评估模型时特别有用，因为模型可能有?requires_grad=True?的可训练的参数，但我们不需要在这个阶段计算梯度。

还有一个类对于 autograd 的实现非常重要：Function。Tensor?和?Function?是互相连接的，并且建立了一个非循环的图，它编码了完整的计算历史。每个张量都有一个?.grad_fn?属性，该属性引用了创建?Tensor?的?Function（除了用户创建的张量——它们的?grad_fn is None）。

如果你想计算导数，你可以调用?Tensor?的?.backward()?方法。如果?Tensor?是一个标量（即它包含一个元素的数据），你不需要为?backward()?指定任何参数，但是如果它有更多的元素，你需要指定一个?gradient?参数，该参数是形状匹配的张量。

让我们看一个简单的例子：

import torch

# 创建一个张量并设置 requires_grad=True 用来追踪它的计算历史
x = torch.ones(2, 2, requires_grad=True)
print(x)

# 对张量进行操作:
y = x + 2
print(y)

# 因为 y 是操作的结果，所以它有 grad_fn 属性。
print(y.grad_fn)

# 对 y 进行更多操作
z = y * y * 3
out = z.mean()

print(z, out)

# 使用 .requires_grad_(...) 改变现有的 Tensor 的 requires_grad 标志。如果没有给出，输入标志默认为 False。
a = torch.randn(2, 2)
a = ((a * 3) / (a - 1))
print(a.requires_grad)
a.requires_grad_(True)
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)

# 梯度，现在开始反向传播，因为 out 是一个标量，因此 out.backward() 等同于 out.backward(torch.tensor(1.)).
out.backward()

# 输出梯度 d(out)/dx
print(x.grad)

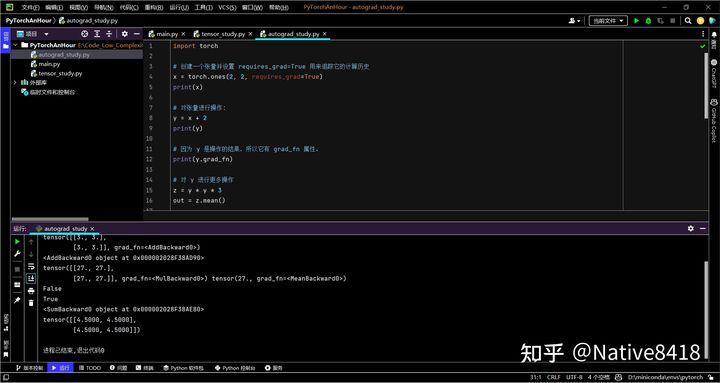
这就是 PyTorch 的 autograd 的基本介绍。在实际使用中，我们通常会将这些操作封装到神经网络模型中，然后使用优化器进行参数的更新。

简单实践

import torch

# 创建大小为(5, 3)的张量，填充随机数
x = torch.rand(5, 3)

# 创建大小为(5, 3)的张量，填充1
y = torch.ones(5, 3)

# 加法运算
z1 = x + y

# 乘法运算
z2 = x * y

# 创建张量并设置requires_grad=True以跟踪计算
v = torch.tensor([[2.0, 3.0], [4.0, 5.0]], requires_grad=True)

# 更复杂的张量计算
z3 = v * v * 3
out = z3.mean()

# 反向传播
out.backward()

# 打印梯度 d(out)/dx
print(v.grad)

# 现在我们将进行更多计算
v2 = v * 2
v2_norm = v2.norm()
v2_norm.backward()

# 打印梯度
print(v.grad)

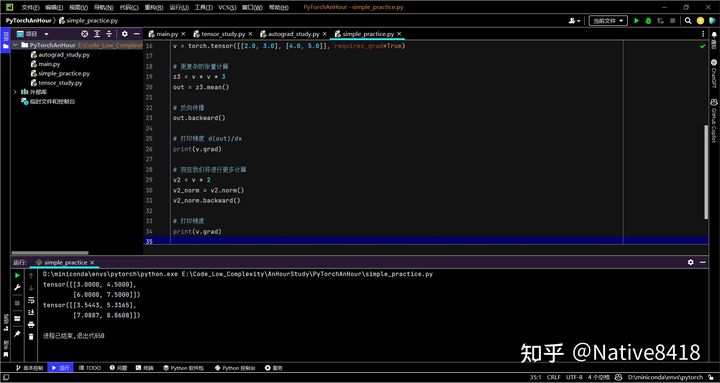
在上面的代码中，我们创建了一些更复杂的张量并对它们进行了操作。

首先，我们创建了两个大小为 (5,3) 的张量?x?和?y。x?是随机初始化的，而?y?是填充了1的张量。然后我们进行了加法和乘法操作，得到了?z1?和?z2。

接着，我们创建了一个大小为 (2,2) 的张量?v，并设置?requires_grad=True?以跟踪其计算。然后我们对?v?进行了更复杂的计算，得到了张量?z3?和?out。z3?是?v?的元素平方乘以3得到的，而?out?则是?z3?的均值。

然后我们对?out?调用了?.backward()，这会计算?out?的梯度。这些梯度存储在原始张量?v的?.grad?属性中。

最后，我们对?v?进行了更多的计算，得到了?v2?和?v2_norm。我们对?v2_norm?进行了反向传播，然后打印出了?v?的梯度。请注意，这次的梯度是累加的，也就是说，新计算的梯度被添加到了先前计算的梯度上。

这段代码展示了如何在 PyTorch 中创建和操作张量，以及如何使用 PyTorch 的自动梯度功能。请注意，虽然这段代码看起来复杂，但其实它的核心只是创建和操作张量，以及使用自动梯度。无论你的神经网络有多复杂，其核心都是这些基本的操作。

简单的神经网络

示例代码

在这个例子中，我们将实现一个简单的全连接神经网络（或多层感知器）来识别 MNIST 数据集中的手写数字。我们将使用 PyTorch 的内置数据集类来加载数据，然后定义一个神经网络模型，最后训练这个模型。

数据集pytorch会自己下载。

以下是实现这个任务的代码：

import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms

# 定义神经网络模型
class Net(nn.Module):
    """定义神经网络模型类"""
    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(28*28, 500)  # 第一个全连接层，输入维度为 28*28，输出维度为 500
        self.fc2 = nn.Linear(500, 10)  # 第二个全连接层，输入维度为 500，输出维度为 10

    def forward(self, x):
        """前向传播方法"""
        x = x.view(-1, 28*28)  # 将输入张量进行展平操作，维度变为 (batch_size, 28*28)
        x = torch.relu(self.fc1(x))  # 使用 ReLU 激活函数进行非线性变换
        x = self.fc2(x)  # 经过第二个全连接层，输出结果
        return x

# 加载 MNIST 数据集
train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),  # 将图像数据转换为张量
                       transforms.Normalize((0.1307,), (0.3081,))  # 归一化处理
                   ])),
    batch_size=64, shuffle=True)  # 每批加载 64 个样本，打乱顺序

test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, transform=transforms.Compose([
                       transforms.ToTensor(),  # 将图像数据转换为张量
                       transforms.Normalize((0.1307,), (0.3081,))  # 归一化处理
                   ])),
    batch_size=1000, shuffle=True)  # 每批加载 1000 个样本，打乱顺序

# 创建模型实例
model = Net()

# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()  # 交叉熵损失函数
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)  # 随机梯度下降优化器

# 训练循环
def train(epoch):
    """训练循环"""
    model.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        optimizer.zero_grad()  # 清零梯度
        output = model(data)  # 前向传播
        loss = criterion(output, target)  # 计算损失
        loss.backward()  # 反向传播，计算梯度
        optimizer.step()  # 更新参数
        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), loss.item()))

# 测试循环
def test():
    """测试循环"""
    model.eval()
    test_loss = 0
    correct = 0
    with torch.no_grad():
        for data, target in test_loader:
            output = model(data)  # 前向传播
            test_loss += criterion(output, target).item()  # 计算测试集损失
            pred = output.data.max(1, keepdim=True)[1]  # 获取预测结果
            correct += pred.eq(target.data.view_as(pred)).sum()  # 计算预测正确的样本数量
    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

# 运行训练和测试
for epoch in range(1, 11):
    train(epoch)  # 训练模型
    test()  # 在测试集上评估模型

在这个代码中，我们首先定义了一个?Net?类，这个类继承自?nn.Module，它是 PyTorch 中所有神经网络模型的基类。我们在?Net?类中定义了两个全连接层（fc1?和?fc2），然后在?forward?方法中定义了如何使用这些层来计算模型的输出。

然后我们加载了 MNIST 数据集，将数据集转换为适合输入到我们的模型中的形式。

接着我们创建了一个?Net?类的实例，定义了一个交叉熵损失函数和一个随机梯度下降优化器。

最后，我们运行了一个训练循环和一个测试循环。在训练循环中，我们将数据输入到模型中，计算出损失，然后使用优化器更新模型的参数。在测试循环中，我们将测试数据输入到模型中，计算出损失，然后计算模型在测试数据上的准确率。

查看数据图片

import torch
from torchvision import datasets, transforms
import matplotlib.pyplot as plt

# 加载 MNIST 数据集
train_data = datasets.MNIST('../data', train=True, download=True,
                            transform=transforms.Compose([
                                transforms.ToTensor(),  # 将图像数据转换为张量
                                transforms.Normalize((0.1307,), (0.3081,))  # 归一化处理
                            ]))

# 获取第一张图像和它的标签
image, label = train_data[0]

# 去除通道维度（因为这是一张灰度图像）
image = image.squeeze()

# 显示图像和它的标签
plt.imshow(image, cmap='gray')
plt.title(f"Label: {label}")
plt.show()

?来源：（一小时实践入门 PyTorch - 知乎）