Binary Tree Right Side View
Problem
Given the?root?of a binary tree, imagine yourself standing on the?right side?of it, return?the values of the nodes you can see ordered from top to bottom.
Example 1:
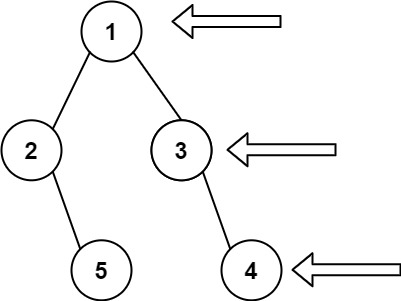
Input: root = [1,2,3,null,5,null,4] Output: [1,3,4]
Example 2:
Input: root = [1,null,3] Output: [1,3]
Example 3:
Input: root = [] Output: []
Intuition
The task is to imagine standing on the right side of a binary tree and returning the values of the nodes visible from that perspective. The intuition is to perform a level order traversal of the binary tree and, for each level, only consider the value of the rightmost node, as that would be the one visible from the right side.
Approach
Initialization:
Check if the root is None. If so, return an empty list since there are no nodes to traverse.
Breadth-First Search (BFS):
Use a queue (in this case, a deque) to perform a breadth-first traversal of the binary tree.
Initialize the queue with the root node.
Right Side View:
While the queue is not empty:
For each level, create a temporary list (temp) to store the values of nodes.
Process all nodes at the current level:
Pop the front node from the queue.
Enqueue its left and right children (if any).
Append the value of the current node to the temp list.
If the temp list is not empty, append the value of the rightmost node to the final result (stack).
Return Result:
Return the final result, which is a list of values representing the nodes visible from the right side.
Complexity
- Time complexity:
The time complexity is O(n), where n is the number of nodes in the binary tree. Each node is visited exactly once during the traversal.
- Space complexity:
The space complexity is O(m), where m is the maximum number of nodes at any level in the binary tree. In the worst case, the maximum number of nodes at any level is the number of leaf nodes, which is at most n/2 in a balanced binary tree. Therefore, the space complexity is O(n/2), which simplifies to O(n) in big-O notation. This is because the space required to store nodes at any level scales with the number of nodes in the tree.
Code
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
stack = [root.val]
q = deque([root])
while q:
temp = []
for _ in range(len(q)):
node = q.popleft()
if node.left:
q.append(node.left)
temp.append(node.left.val)
if node.right:
q.append(node.right)
temp.append(node.right.val)
if temp:
stack.append(temp[-1])
return stack本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Spring简介
- 每日好文1 What‘s the Future of Train Operators?
- shell备份文件(这里备份文件到天翼云对象存储(并行文件系统))
- SAP SQVI制作报表及SE93创建事务代码
- AI分割一切模型SAM(Segment Anything Model)的C++部署
- Python算法例29 统计比给定整数小的数
- Zookeeper集群 + Kafka集群
- 23 年终总结:生活是一场永无止境的探索
- 这款APP注册即可查看、编辑及分享三维模型、点云等数据
- 第七次全国人口普查数据