基于格理论来破解RSA公钥密码（2）

发布时间：2024年01月22日

目录

一. 基于格密码求解模多项式的根

1.1 如何求解模多项式的根

1.2 优化

1.3 进一步优化

小结

一. 基于格密码求解模多项式的根

在本小节中，我们将分成三步来解释如何利用格密码来求解模多项式的根。在此过程中，大家可以体会到格密码的应用非常广泛。除了可以自己形成加密或签名系统，也可以用来攻击其他的密码系统。

本文章属于系列文章的第二篇，第一篇的链接已附在结尾。

第一步证明B的界限如下：

\Theta(N^{\frac{2}{d(d+1)}})

其中\Theta中省略了有关于d的系数部分，因为d代表多项式的次数，所以相当于省略了常数部分。

接着将B的界限优化到：

\Theta(N^{\frac{1}{2d-1}})

最终优化到：

B=N^{1/d}

在接下来的讨论中，大家可以把d想象成一个很小的常数，比如像d=3这类。

1.1 如何求解模多项式的根

给定如下次数为d的多项式：

我们的目标是希望寻找如下方程的解x：

f(x)=0\quad mod\ N

且要求x的绝对值不能太大，也就是需要满足：

|x|\leq B

很明显如果B越小的话，这样的解越不好找，这也是解释了为什么最开始我们需要经历三次优化过程。

需要注意的是，这个问题需要模运算，也加大了其求解难度。我们先来看一个特殊的例子。

如果多项式的系数都比较小，比如满足如下：

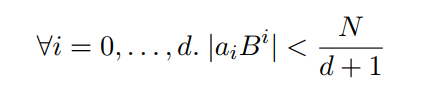
对任意|x|<B，该多项式的取值一定有上限，且上限一定小于N，可得：

|f(x)|\leq \sum_{i=0}^d|a_iB^i|<N

也就是有没有模N运算，结果是一样的。换句话说f(x)=0? mod N的解与单纯f(x)=0的解是一样的。如果能求出了一个，另一个也就可以求了。

如果没有模运算的话，我们知道f(x)=0的解一定有d个，那么直接找出所有符合的解，并保留整数解，就可以了。

如果以上要求不成立，怎么办？

接下来将是本文章的精髓，也是为什么此类问题可以跟格理论进行结合：

当f的多项式系数不满足如上条件时，那么求解x将是困难的。但是，我们可以将f乘以某个整数，然后再mod N，此过程相当于对系数进行重组，一共有N个整数可以乘，那么应该会存在至少一种结果符合我们的要求，也就是该多项式的系数都相对较小。

接下来，我们希望寻找到一个新的多项式g，来保证该多项式和f拥有一样的根。这样的话，当我们求出多项式g所有的根的时候，也就可以寻找到满足多项式f的小根。来看一个有关多项式的集合：

很显然，对这些多项式进行整数倍的组合，在mod N下与原始的多项式f的根是一样的。这个地方的整数倍组合，不就是对格基进行整数倍组合，这不就是格密码！！

接下来我们的重心则是关注如何对这些多项式进行整数倍组合来保证其满足如上性质。首先可形成如下格：

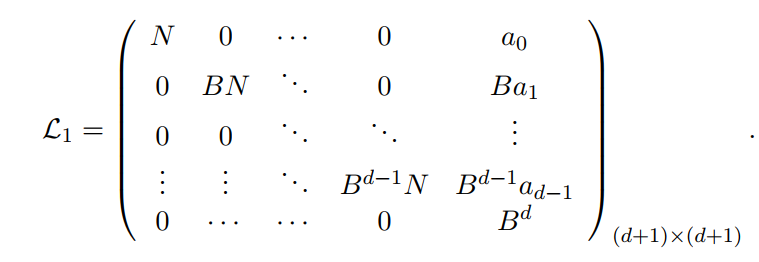
很明显该矩阵的每一列都对应Z_1中的一个多项式，一共有d+1行，如下：

i=0,\cdots,d

第i行代表x^i的系数乘以B^i，再模N。

我们的目标是在此格中寻找短向量。首先，格的行列式与格基矩阵的行列式计算是一样的，如下：

上三角矩阵的行列式即为对角线处元素相乘。

LLL格基约化可以将格基的长度变短。在此处可以简单回顾LLL格基约化的定理：

注意以上定理中的n为格的维度，在此处即n=d，于是乎我们可以得到：

以上式子中的v即为我们要找到的短格向量。

第一个不等式即为LLL格基约化定理，注意前面d的运算在此处为常数，所以被省略了，用O()代替。

第二个不等式是Minkowski定理，可以快速回顾下：

省略前面的系数，带入即可得。

第三个等式：带入格的行列式

如果我们对B的长度，限定为如下：

B\leq c_1(d)N^{\frac{2}{d(d+1)}}

其中c1(d)为很小的数，且只跟d有关，由此可得v的长度满足：

|v|\leq \frac{N}{d+1}

换句话说，我们也可以得到v的每一个系数都要小于N/(d+1)

借助以上理论，我们从多项式集合Z1中寻找到了一种整数组合方式，得到一个新的多项式：

该多项式的系数相对较小，也就是满足：

\forall i=0,\cdots,d\quad |b_iB^i|<\frac{N}{d+1}

此时对多项式g(x)来讲便可以将模N直接去掉，那么可以使用一些标准的方法来求解多项式g的所有小正数解根。

又因为多项式g与多项式f的解是一样的，此问题描述结束。

1.2 优化

我们来看一个更大的多项式集合，如下：

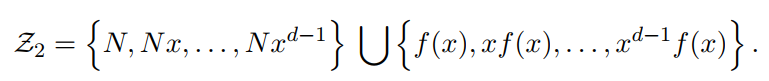
对如上多项式进行整数倍组合，形成新的多项式g，实际上该多项式g包含所有多项式f的根。当然需要注意的是，g可能含有比f更多的根，但只要把g的根全部找出来，f也就解决了。

由此可形成如下格基：

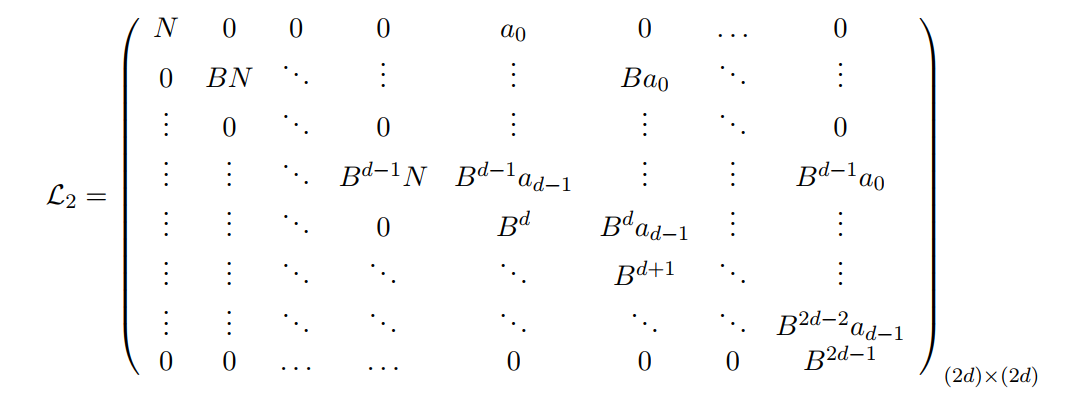
模仿刚才的过程，也同样使用LLL格基约化过程，由此可得一个格向量v其长度满足：

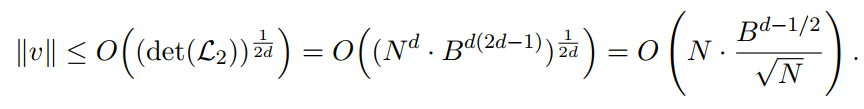
接下来，我们可以对上界B选择：

B\leq c_2(d)N^{\frac{1}{2d-1}}

其中c2(d)为一个很小的数。借助此边界可以让格向量v的长度小于N/2d。简单解释就是对多项式集Z2中的多项式进行整数倍组合时，可以形成v。

多项式g的次数是2d-1，且一定满足：

\forall i=0,\cdots,2d-1\quad |b_iB^i|<\frac{N}{2d}

现在便可以直接在整个整数域上求取多项式g的短解。

1.3 进一步优化

接下来我们调整让f(x)和g(x)在模不同的数，也就是原来的多项式为：

f(x)=0\quad mod\ N

转变为：

g(x)=0\quad mod\ N^{h-1}

其中h为大于等于2的整数，如下：

h\geq 2

由此现在多项式的集合如下：

我们发现当h=2时，其实就跟前一种情况是一模一样的。

如果对以上多项式进行整数倍组合，则可以形成新的多项式g(x)。

运用同样的方法，可以设定h适当大一点，对任意的：

\epsilon>0

可得：

B=N^{\frac{1}{d}-\epsilon}

比如可以取B的上限为：

B=10N^{1/d}
以上问题便可以同样解决。

小结

在网络安全领域，本过程可用于攻击RSA公钥密码系统。

系列文章：

基于格理论来破解RSA公钥密码（1）-CSDN博客

文章来源:https://blog.csdn.net/forest_LL/article/details/135752416
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章