CGAL的3D Alpha Shapes

????????假设我们给定一个二维或三维的点集S,我们希望得到类似“这些点形成的形状”的东西。这是一个相当模糊的概念,可能有许多可能的解释,阿尔法形状就是其中之一。阿尔法形状可用于从密集的无组织数据点集进行形状重建。事实上,阿尔法形状是由一个边界划分的,该边界是原始形状的线性近似。
????????正如Edelsbrunner和Mücke的论文中所提到的,我们可以直观地将α形状想象成以下形状。想象一个巨大的冰淇淋块占据了空间R3,并将点作为“硬”巧克力块。使用其中一个球形冰淇淋勺,我们挖出了冰淇淋块的所有部分,我们可以在不碰到巧克力块的情况下挖出冰淇淋块的所有部分,从而甚至可以在内部挖出孔(例如,通过从外面移动勺子无法到达的部分)。我们最终会得到一个由帽、弧和点界定的(不一定是凸的)物体。如果我们现在将所有“圆形”面拉直为三角形和线段,我们就可以直观地描述所谓的S的α形状。上图提供了二维过程的一个例子(我们的冰淇淋勺只是一个圆)。
????????α 形状取决于一个参数 α,之后它们被命名。 在上面的冰淇淋类比中,α 是雕刻勺的平方半径。 一个非常小的值将允许我们吃掉所有的冰淇淋,除了巧克力点本身。 因此,我们已经看到 α 形状在 α→0 时退化为点集 S。 另一方面,α 的巨大值将阻止我们甚至在两点之间移动勺子,因为它太大,我们永远不会用勺子舀起位于 S 的凸包内部的冰淇淋。 因此,α 形状在 α→∞ 时变成 S 的凸包。
????????CGAL提供了2D和3D的Alpha图形。GUDHI库提供了一个dD Alpha复合体。
1、定义
????????我们区分两种α形状。基本的alpha形状基于Delaunay三角剖分。加权阿尔法形状是基于它的推广,即正三角剖分(参见Section regular Triangulations),用加权点的幂代替欧氏距离。
让我们考虑Delaunay三角剖分的基本情况。
????????我们首先定义了点集S的阿尔法复形。阿尔法复形是Delaunay三角测量的一个子复形。对于给定的α值,α复形包括Delaunay三角测量中的所有单形,这些单形具有平方半径等于或小于α的空外接球。这里的“空”意味着开球不包括S的任何点。阿尔法形状就是阿尔法复形的单形所覆盖的域。
????????一般来说,阿尔法复形是一种不连续的非纯复形,这特别意味着阿尔法复形可能具有奇异面。对于0≤k≤d?1,如果α复形的k-单纯形不是该复形的(k+1)-单纯形的一个方面,则称其为奇异的。
????????CGAL提供两种阿尔法形状。在一般模式中,阿尔法形状严格对应于上述定义。正则化模式提供阿尔法形状的正则化版本。它对应于阿尔法复形的正则化版本所覆盖的域,其中奇异面被去除。

????????一般和正则阿尔法形状的比较。左:一些点取在圆环体的表面上,三个点取在离圆环体表面相对较远的地方;中间:一般的阿尔法形状(对于足够大的阿尔法值)包含三个孤立点的奇异三角形面;右:正则化版本(对于相同的alpha值)不包含任何奇异方面。?
????????一组点S的α形状形成了一个离散族,即使它们是为所有实数α定义的。整个α形状族可以通过S的底层三角剖分来表示。在这种表示中,底层三角剖分的每个k-simplex与一个区间相关联,该区间指定了k-simplex属于α复体的α值。基于这一事实,α形状族可以高效且相对容易地计算。此外,我们可以选择最佳α值来获得一个包含所有数据点并且具有小于给定数量的连通分量的α形状。此外,α值允许对一组点的三角剖面的面进行过滤。在这种过滤中,三角剖面的面以α值的升序输出,这些α值出现在α复体中。在α值相等的情况下,首先输出低维面。
????????在加权α形状的情况下,定义是模拟的。输入集现在是一组加权点(可以看作球体),底层三角剖分是这个集合的规则三角剖分。两个球体或两个加权点,中心C1、C2和半径r1、r2,如果C1C22=r21+r22,则称为正交,如果C1C22<r21+r22,则称为次正交。对于给定的α值,加权α复形由规则三角剖分的单形形成,使得有一个球体与单形的顶点相关的加权点正交,并与所有其他输入加权点次正交。然后,α形状被定义为α复形覆盖的域,通常有规则版本。
2、功能
2.1、Alpha形状族
????????类Alpha_shape_3<Dt,ExactAlphaComparisonTag>表示给定点集的整个alpha形状家族。该类包括该集合的基础三角剖分Dt,并将该三角剖分的每个k面与一个区间相关联,该区间指定该面属于alpha复体的α值。第二个模板参数ExactAlphaComparisonTag是一个标记,当设置为CGAL标准库中的Tag_true时,会触发alpha值之间的精确比较。
????????该类提供设置和获取当前α值的函数,以及枚举α值(alpha形状变化的位置)的迭代器。
????????此外,该类具有一个过滤成员函数,该函数给定一个以Object为值类型的输出迭代器,当alpha增加时,根据alpha复合体中出现的顺序输出三角形的面。
????????最后,它提供了一个函数来确定最小值α,使得alpha形状满足以下两个属性:
????????所有数据点要么在边界上,要么在alpha形状正则化版本的内部(没有奇异面)。
????????组件的数量等于或小于给定的数量。
????????当前的实现是静态的,也就是说在构造后,点不能被插入或删除。
2.2、?Alpha Shape for a Fixed Alpha
????????给定alpha值,类Fixed_alpha_shape_3<Dt>表示给定点集的一个alpha形状。该类包括集合的基础三角测量Dt,并将分类类型关联到该三角剖分的每个k面。此类是动态的,即在可以插入或删除其构造点之后。
2.3、分类和迭代
????????这两个类都提供了成员函数,用于将三角形的不同面相对于α形状分类为EXTERIOR、SINGULAR、REGULAR或INTERIOR(给定)α值。α复形边界上的k面被称为:REGULAR,如果它是α复形的子面,α复形是α复形(k+1)面的子面,否则是SINGULAR。不在α复形边界上的α复形的k面被称为INTERIOR。二维图示见图。
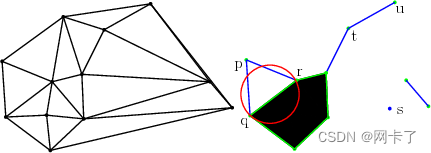
?????????这些类还提供输出迭代器,用于为给定的alpha值获取不同类型(EXTERIOR、SINGLUAL、REGULAR或INTERIOR)的顶点、边、面和单元。
2.4、输入和输出
????????可以使用运算符<<将3D alpha形状导出到std::ostream,有关更多信息,请参阅类alpha_shape_3的文档。?
3、概念与模型
????????我们目前没有为基础三角剖分类型指定概念。适用于alpha形状族的模型是类Delaunay_triangulation_3和Periodic_3_Delanay_trianglation_3的实例化(请参见周期性alpha形状的示例)。适用于固定alpha形状的模型是类Delaunay_triangulation_3的实例。适用于加权阿尔法形状的模型是类Regular_triangulation_3和Periodic_3_Regular _trianguulation_3的实例化。三角剖分需要一个几何特征类和一个三角剖分数据结构作为模板参数。
3.1、?Alpha Shapes
????????对于类Alpha_shape_3<Dt,ExactAlphaComparisonTag>,特征类的要求在非加权情况下的概念AlphaShape Traits_3和加权情况下的概念WeightedAlphaShape Traits_3中进行了描述。所有CGAL内核都是这两个概念的模型。
????????三角剖分的三角剖分数据结构必须是概念 TriangulationDataStructure_3 的模型,其顶点和单元类是概念 AlphaShapeVertex_3 和 AlphaShapeCell_3 的模型。类 Alpha_shape_vertex_base_3<Gt>?和 Alpha_shape_cell_base_3<Gt>?是这些概念的模型,可用于所有类型的 alpha 形状,只要适当地选择模板参数 Vb 和 Fb,正如我们将在下一节中看到的那样。
3.2、固定的Alpha形状
????????对于类 Fixed_alpha_shape_3<Dt>,特征类的要求在非加权情况下的概念 FixedAlphaShape Traits_3 和加权情况下的概念 FixedWeightedAlphaShape Traits_3 中进行了描述。所有 Ridge 核都是这两个概念的模型。三角剖分的三角剖分数据结构必须是概念 TriangulationDataStructure_3 的模型,其顶点和单元类是概念 FixedAlphaShapeVertex_3 和 FixedAlphaShapeCell_3 的模型。该软件包分别提供了模型 Fixed_alpha_shape_vertex_base_3<Gt>?和 Fixed_alpha_shape_cell_base_3<Gt>。
3.3、三角剖分的数据结构
????????当使用加权或周期三角剖分作为基础三角剖分时,需要额外的要求:
????????使用加权三角剖分(Regular_triangulation_3 或 Periodic_3_regular_triangulation_3)时,顶点和单元类必须分别是 AlphaShapeVertex_3 和 RegularTriangulationVertexBase_3 的模型,以及 AlphaShapeCell_3 和 RegularTriangulationCellBase_3 的模型。
????????使用周期三角剖分(Periodic_3_Delaunay_triangulation_3 或 Periodic_3_regular_triangulation_3)时,顶点和单元类必须分别是 AlphaShapeVertex_3 和 Periodic_3TriangulationDSVertexBase_3 的模型,以及 AlphaShapeCell_3 和 Periodic_3TriangulationDSCellBase_3 的模型。
4、Alpha_shape_3与Fixed_Alpha_shape_3
????????类Alpha_shape_3<Dt,ExactAlphaComparisonTag>表示给定点集的整个alpha形状家族,而类Fixed_alpha_shape_3<Dt>仅表示一个alpha形状(对于固定的alpha)。
????????在使用相同的内核时,Fixed_alpha_shape_3<Dt>是更轻量级的版本。因此,当需要一个特定值的alpha的alpha形状时,它自然更加高效。
????????此外,请注意,类Alpha_shape_3<Dt,ExactAlphaComparisonTag>需要构造(简单x的平方半径),而类Fixed_alpha_shape_3<Dt>仅使用谓词。这意味着使用Alpha_shape_3<Dt,ExactAlphaComparisonTag>进行认证的构造(一个或多个alpha形状)需要具有精确谓词和精确构造的内核(或将ExactAlphaComparisonTag设置为Tag_true),而使用具有精确谓词的内核对于Fixed_alpha_shape_3<Dt>就足够了。
????????这使得Fixed_alpha_shape_3<Dt>在这种设置下更加高效。此外,请注意,固定版本是两个中唯一支持逐点插入和删除的版本。
????????我们给出在计算具有4251个原子的蛋白质(作为一组加权点)的alpha形状时花费的时间(使用gcc 4.3在Linux上,带有-O3和-DNDEBUG标志,在2.27GHz Intel(R) Xeon(R) E5520 CPU上):
????????使用Exact_predicates_inexact_constructions_kernel,构建常规三角剖分需要0.09s,然后使用类Fixed_alpha_shape_3<Dt>需要0.05s,而使用类Alpha_shape_3<Dt,ExactAlphaComparisonTag>(如果ExactAlphaComparisonTag为Tag_false)需要0.35s(使用Tag_true为0.70s)。
????????使用Exact_predicates_exact_constructions_kernel,构建常规三角剖分需要0.19s,然后使用类Alpha_shape_3<Dt,ExactAlphaComparisonTag>需要0.90s。
5、其他
????????当许多点以阿尔法形状输入时,例如超过10000个,使用Delaunay三角剖分和Fast_location策略作为基础三角剖分可能会有回报,以加快点位置查询。
????????CGAL::Alpha_shape_3 是CGAL库中的一个类,用于构建和操作α形状。α形状是一种将三维空间中的点云数据转换为多面体的数据结构,可用于进行形状分析、表面重建等任务。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!