运算电路（1）——加法器

一、引言

????????微处理器是由一片或少数几片大规模集成电路组成的中央处理器。这些电路执行控制部件和算术逻辑部件的功能。微处理器能完成取指令、执行指令，以及与外界存储器和逻辑部件交换信息等操作，是微型计算机的运算控制部分。它可与存储器和外围电路芯片组成微型计算机。微处理器（CPU、MCU、DSP、GPU、NPU等）是最重要的一类集成电路，没有之一。其构成如下图所示：

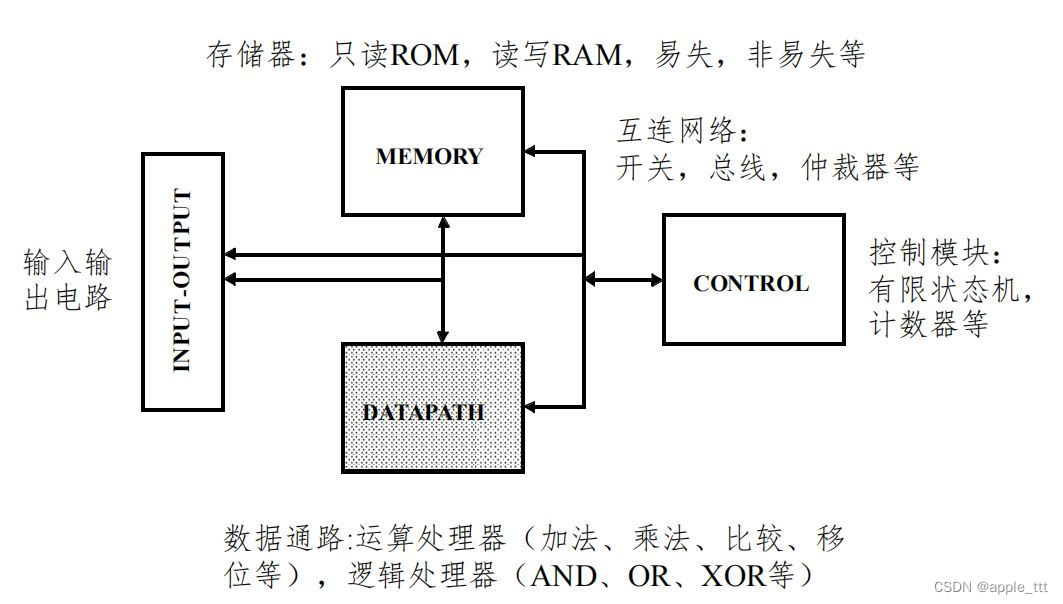
? ? ? ? 其中数据通路的构成如下：

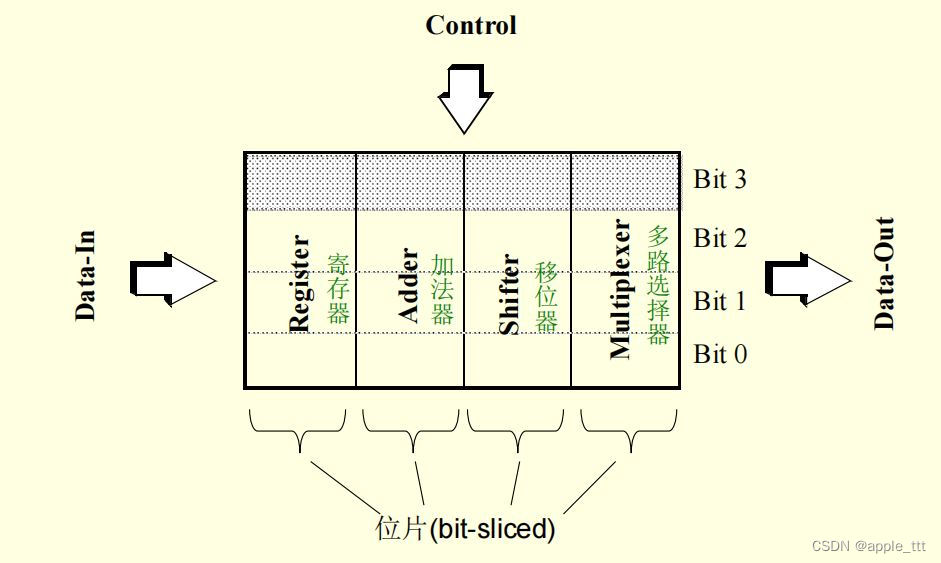
? ? ? ? 本文就主要介绍数据通路的相关内容，包括其中的各种复杂运算单元。

二、加法器：一位

2.1 半加器

????????半加器作为一个非常经典的电路设计是初学者避不开的一个话题。其本质就是实现了不带进位输入的二进制加法运算，其真值表如下

a	b	carry	sum
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

????????根据真值表我们可以很容易得出：

????????????????????????????????????????????????????????????????carry = a & b ;

????????????????????????????????????????????????????????????????sum = a ^ b ;

????????对应的电路结构如下:????????

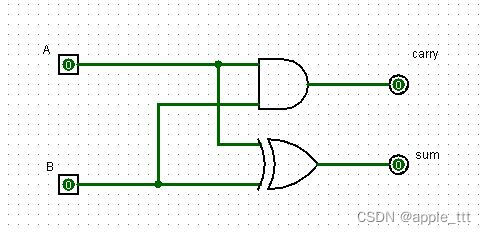
????????对应真值表不同的输入情况如下：

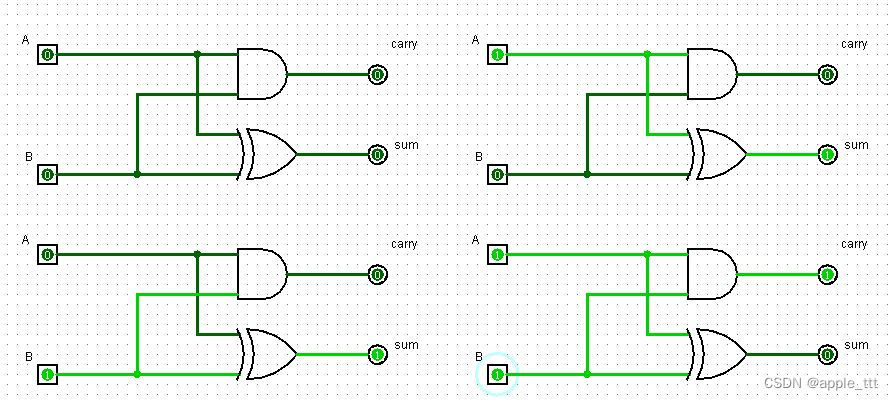
2.2 全加器

????????有了半加器我们就解决了一位二进制数的加法问题，但是这显然还是不够的，要想实现多位二进制数的加法问题，我们就必须在现有电路的基础上进行改进，首先就是要引入进位输入。

? ? ? ? 和之前一样，我们还是先给出真值表

A	B	Cin	Sum	Cout
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

? ? ? ? ?根据真值表给出逻辑式：
?????????????????????????????????????????????????Sum = A ^ B ^ Cin;
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?Cout = ( A & B ) | (( A ^ B ) & Cin);

? ? ? ? 其静态CMOS管实现如下：

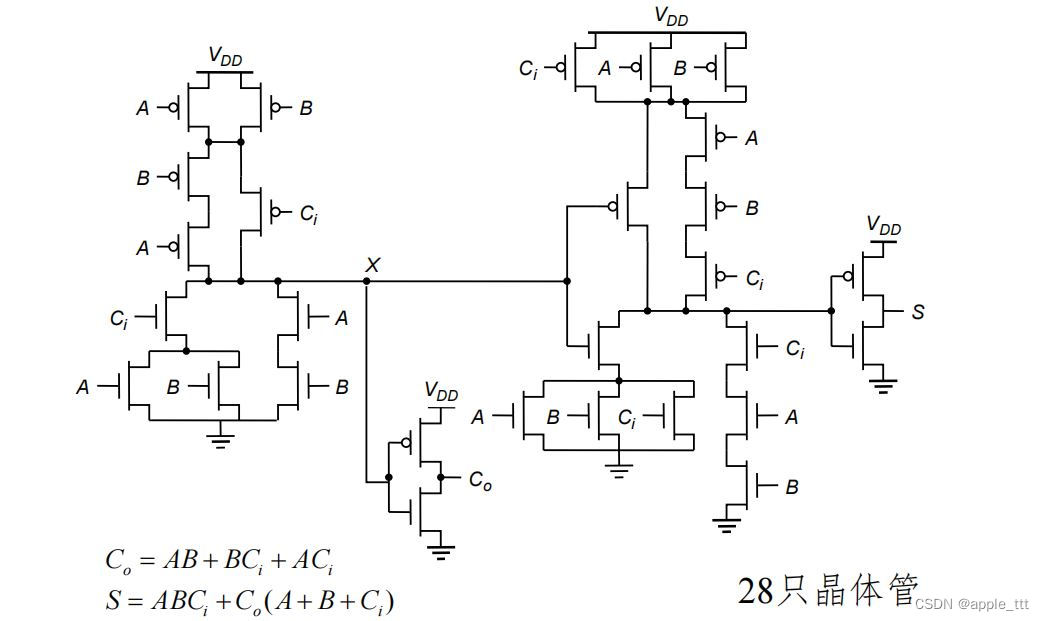
? ? ? ? 对于这样的加法器，我们还是希望能够进行进一步的优化，优化的方向有2个：（1）提高速度（2）缩小面积

? ? ? ? 优化的途径如下：

• 逻辑层优化：重新安排布尔方程
• 结构层优化：调整整体拓扑结构
• 电路级优化：优化管级电路
• 器件级优化：优化晶体管尺寸

三、加法器：多位

3.1 串行进位加法器

3.1.1 构成

????????串行进位加法器亦称传播进位加法器（Carry-Propagate Adder，CPA）、行波进位加法器（ripple carry adder）。我们以搭建一个4位的加法器为例，这种加法器的设计思路非常的简单，就是把上一个加法器的进位连接到下一个加法器的进位输入端，具体的设计电路如下：

3.1.2 HDL描述

3.1.3 传播延时

? ? ? ? 对于串行进位加法器来说，其关键路径如下图所示：?

????????延时计算：tadder_4=t(A0 ,B0→ Co,0 )+t(Co,0 →Co,1 ) +t(Co,1 →Co,2 )+t(Co,2 →S3 )

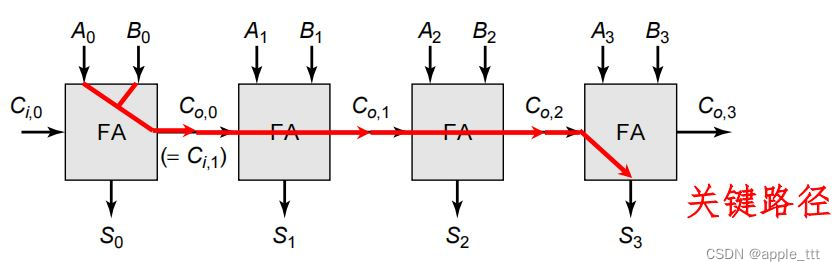
? ? ? ? 它的电路延时与输入值有关。最坏情况之一：A=0001，B=0111。对于N位的串行进位加法器来说，传输延时与位数成线性正比关系，位数越多运算越慢；加法器序列的延时受“进位”计算项而非“和”计算项支配，因此如何缩短“进位”链延时是关键。

3.2 超前进位加法器

3.2.1 理解

????????针对串行进位加法器运算速度慢的问题，有人就提出了超前进位加法器的概念。要理解超前进位加法器的原理，我们需要换一个角度来看全加器：

? ? ? ? 一个全加器的输入有：数据A、数据B、前级的进位Cin，输出有：和S、进位Cout。我们要做的就是根据对应的输入给出对应的输出。我们知道限制串行进位加法器运算速度的主要问题是进位的运算。这里我们考虑Cout的运算，如果A=B=0，那么无论Cin是0或1，都不会产生进位，所以Cout恒等于0，我们称这种情况为取消（D）；如果A=B=1，那么无论Cin是0或1，都会产生进位，所以Cout恒等于1，我们称这种情况为产生（G）；如果A和B中有且只有一个为0，那么无论Cout就取决于Cin，Cout = Cin，我们称这种情况为传播（P）。

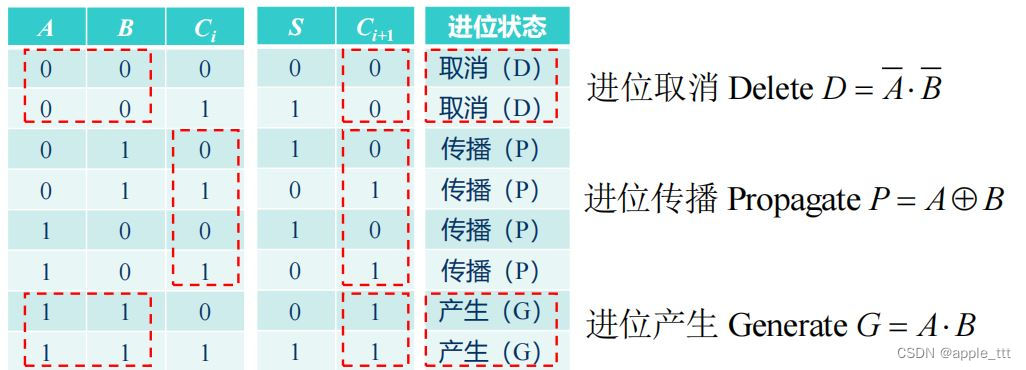
? ? ? ? 这样一来，原来的计算公式就可以进行如下变换：

? ? ? ? 基于此完成公式的递推：

3.2.2 HDL描述

3.3.3 逻辑门实现

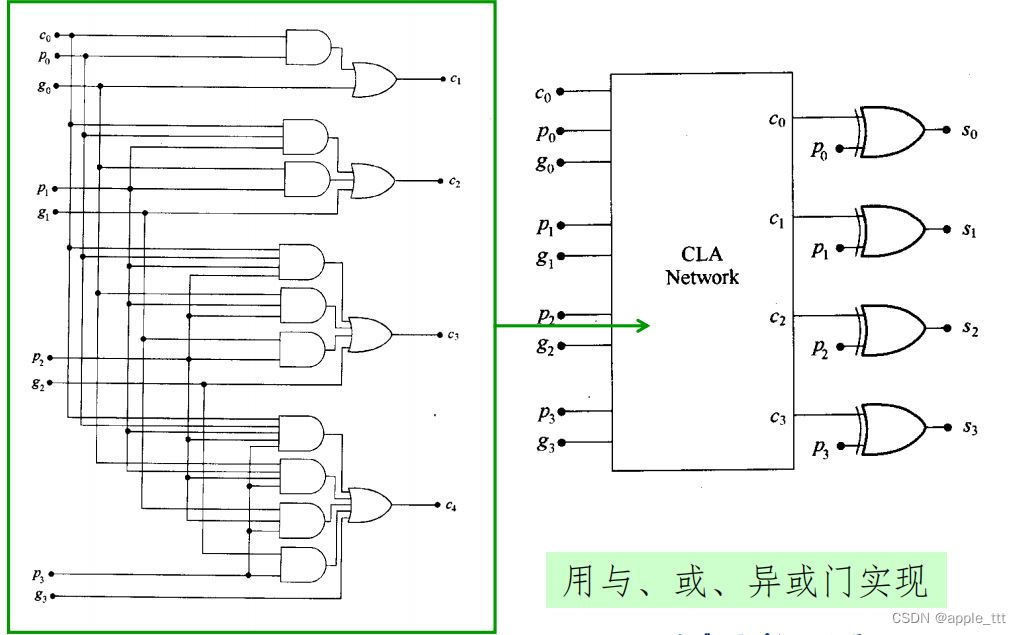
3.3.4 nFET实现

3.3.5 不足

? ? ? ? 采用超前进位加法器似乎做到了快速计算的效果，但是却存在扇入过大，使得N值较大时很慢； 扇出过大，亦会显著加大延迟；实现面积随N的增加而快速增加的问题，因此一般适用于N≤4的情况。

3.3 曼彻斯特加法器

3.3.1 原理

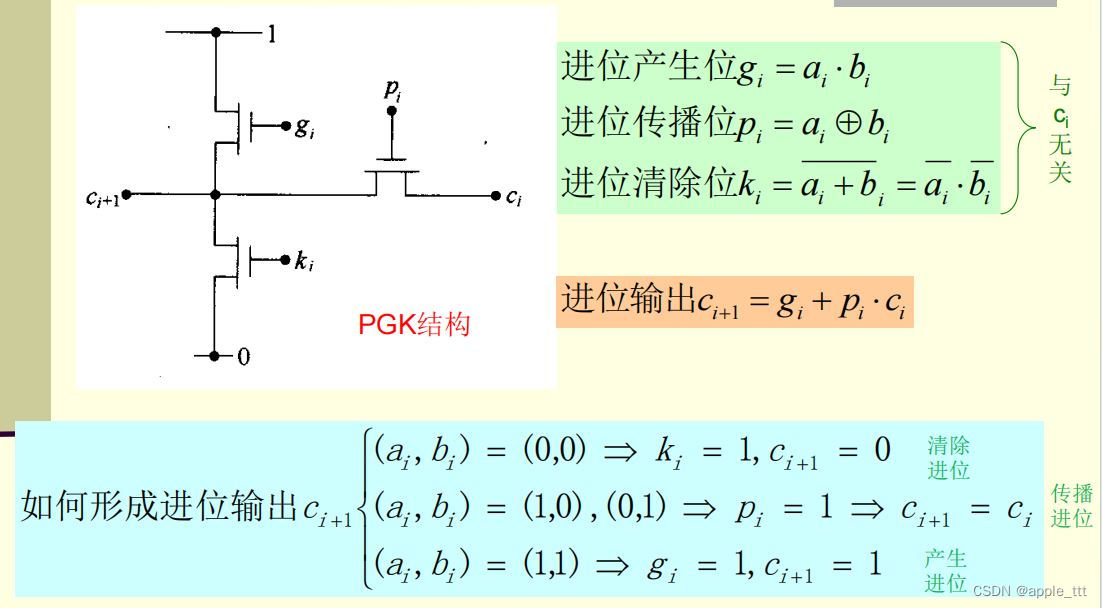
3.3.2 电路结构

????????对于上图中的电路，每一时刻有且只有1个FET是导通的。考虑到p,g,k只能有一个为1，可以变换电路结构：

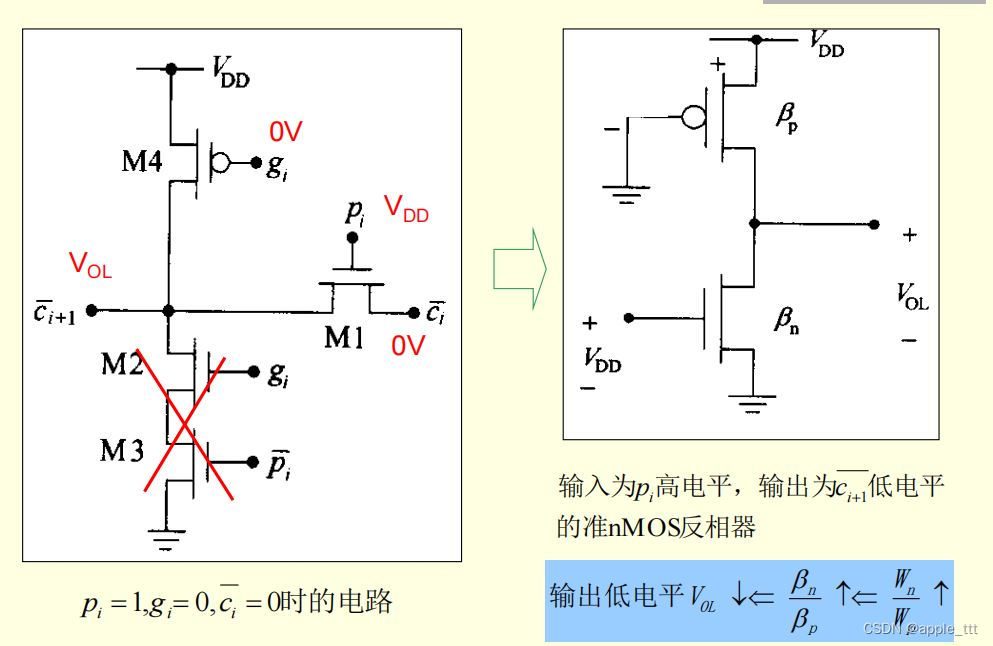
3.3.3 动态CMOS

? ? ? ? 可以采用动态CMOS实现上述电路：

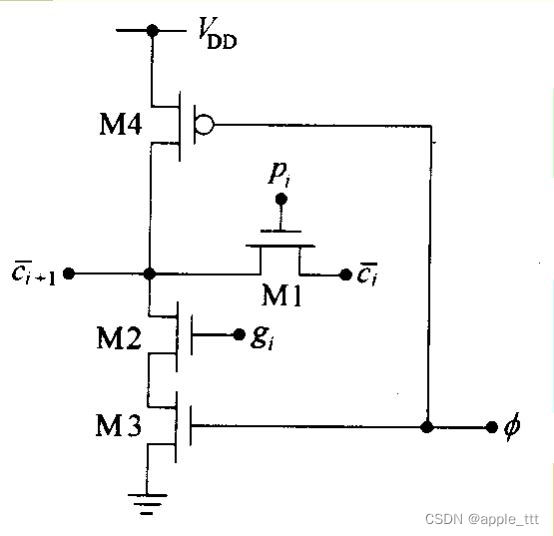
• 预充电（＝0） ?M4导通， M3截止；对负载电容充电，输出被拉至逻辑1
• 求值（＝1）M4截止， M3导通；

3.3.5 延迟分析

• 进位链的延时与链长N的平方成正比，即曼彻斯特链减少了每一级的延时（RC），与N的敏感性却增加了。因此，曼彻斯特进位链一般不超过四阶，常作为宽位加法器的基本运算单元
• 插入缓冲器可以降低进位链的总延迟，并使延时正比于N。 插入缓冲器的最佳级数取决于反相器的等效电阻及传输管的RC，通常为3～4级

3.4 宽位加法器

? ? ? ? 在如今的电子设备中，大多数都是宽位计算机，例如台式计算机多为32bit/64bit、服务器多为64bit、大型机及超级机可达128bit。这就会导致位数↑→通过最长时延路径的门数↑→最高进位计算时延↑→进位链的总延时↑。因此我们需要使宽位加法器的进位链长度平摊→多层（多级）CLA电路。

? ? ? ? 我们以基于4位超前进位加法器的宽位加法器为例：

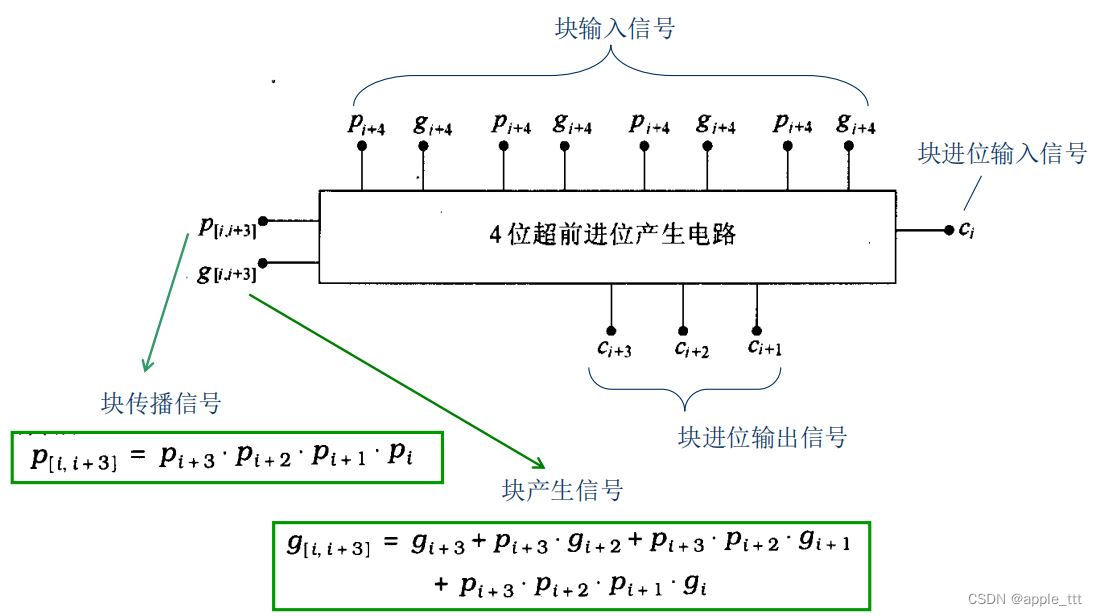
? ? ? ? 它的传播延时计算如下：

3.5 进位旁路加法器

3.5.1 原理

????????Carry-Bypass Circuits：在一定条件下，使进位绕过加法器的一部 分进行传播，用于宽位加法器的加速。

3.5.2 延时分析

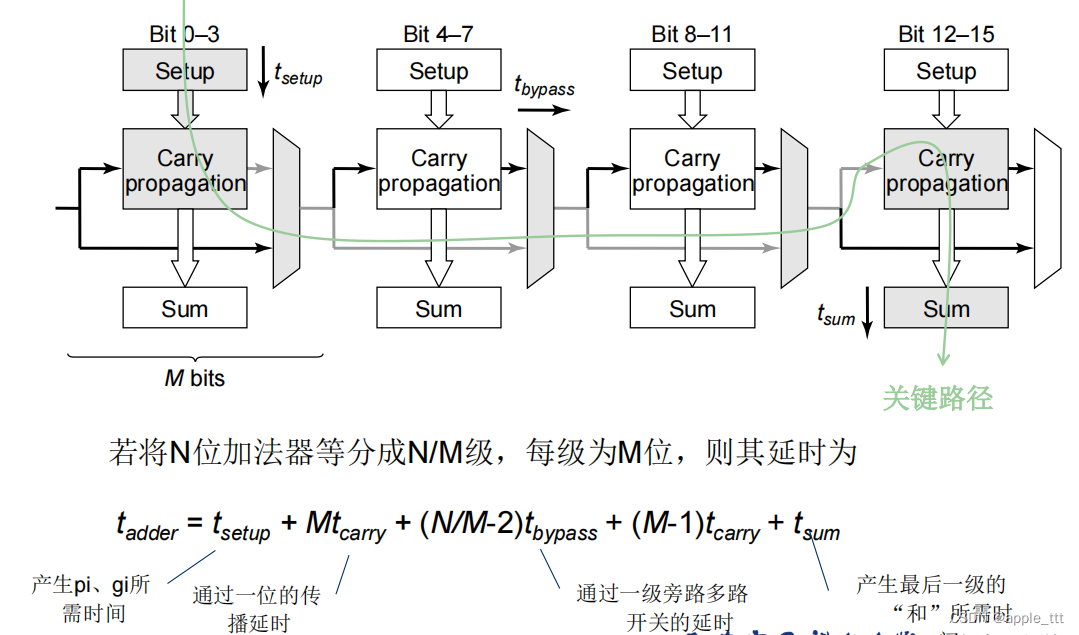
3.6 进位选择加法器

????????Carry-Select Adder：采用多个位数较少的加法器，通过 进位选择的方式来构成快速的宽位加法器。