【视觉SLAM十四讲学习笔记】第四讲——指数映射

专栏系列文章如下：
【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍
【视觉SLAM十四讲学习笔记】第二讲——初识SLAM
【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵
【视觉SLAM十四讲学习笔记】第三讲——旋转向量和欧拉角
【视觉SLAM十四讲学习笔记】第三讲——四元数
【视觉SLAM十四讲学习笔记】第三讲——Eigen库
【视觉SLAM十四讲学习笔记】第四讲——李群与李代数基础

现在来到第二个问题：如何计算exp(φ^)？

指数映射

SO(3)上的指数映射

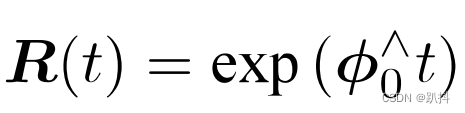
前一篇文章提到：上式前提是R在原点附近的一阶泰勒展开，我们看到这个向量φ=（φ1，φ2，φ3）反应了R的导数性质，故称它在SO(3)上的原点 φ_0 附近的正切空间上。这个φ正是李群大SO(3)对应的李代数小so(3)。换言之，李代数小so(3)是三维向量φ的集合，每个向量φ_i的反对称矩阵都可以表达李群（SO(3)）上旋转矩阵R的导数，而R和φ是一个指数映射关系。也就是说，李群空间的任意一个旋转矩阵R都可以用李代数空间的一个向量的反对称矩阵指数来近似。用旋转矩阵表示的话就是李群空间。而用向量的反对称矩阵表示的话就是李代数空间，这两个空间建立了联系。

话说回来：任意矩阵的指数映射可以写成一个泰勒展开，但是只有在收敛的情况下才会有结果，其结果仍是一个矩阵：

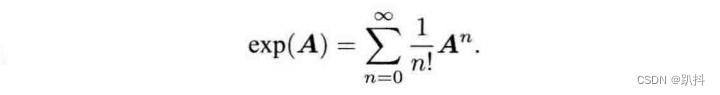
同样地，对so(3)中的任意元素φ，我们也可按照此方式定义它的指数映射：

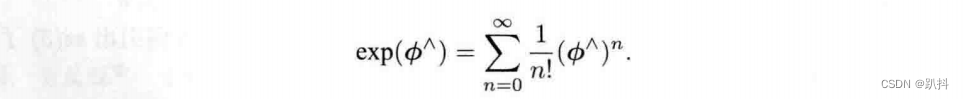
设三维向量 φ = θa，a是一个长度为1的方向向量，θ是向量的方向。通过运用泰勒展开以及反对称矩阵的性质，我们可以得到如下结果（推导过程省略）：

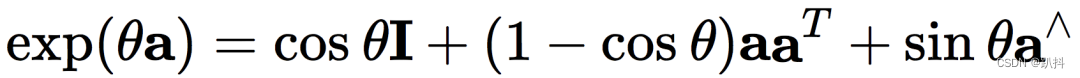
这条式子和罗德里格斯公式一模一样。这表明：so(3)的李代数空间就是由旋转向量组成的的空间，其物体意义就是旋转向量，而指数映射即罗德里格斯公式。罗德里格斯公式是表示从旋转向量到旋转矩阵的转换过程。通过它们，我们把so(3)中任意一个向量对应到了一个位于SO(3)中的旋转矩阵。反之，如果定义对数映射，也能把SO(3)中的元素对应到so(3)中：

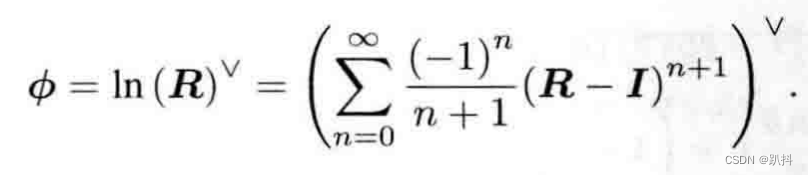
话说回来，是否对于任意的R都能找到一个唯一的φ？很遗憾，指数映射只是一个满射而非单射。这意味着每个SO(3)中的元素，都可以找到一个so(3)的元素与之对应；但是可能存在多一个so(3)中的元素，对应到同一个SO(3)。至少对于旋转角θ，我们知道多转360°和没有转是一样的——它具有周期性。但是如果把旋转角度固定在±π之间，那么李群和李代数元素是一一对应的。

SE(3)上的指数映射

se(3)上的指数映射形式如下：

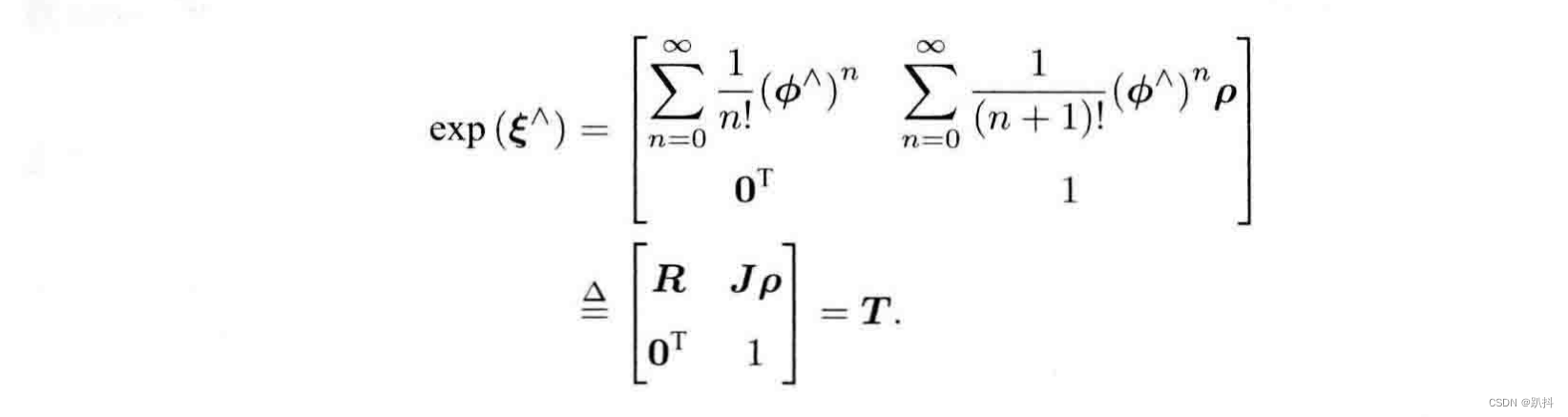
把exp进行泰勒展开推导此式，令φ = θa，其中a为单位向量，则

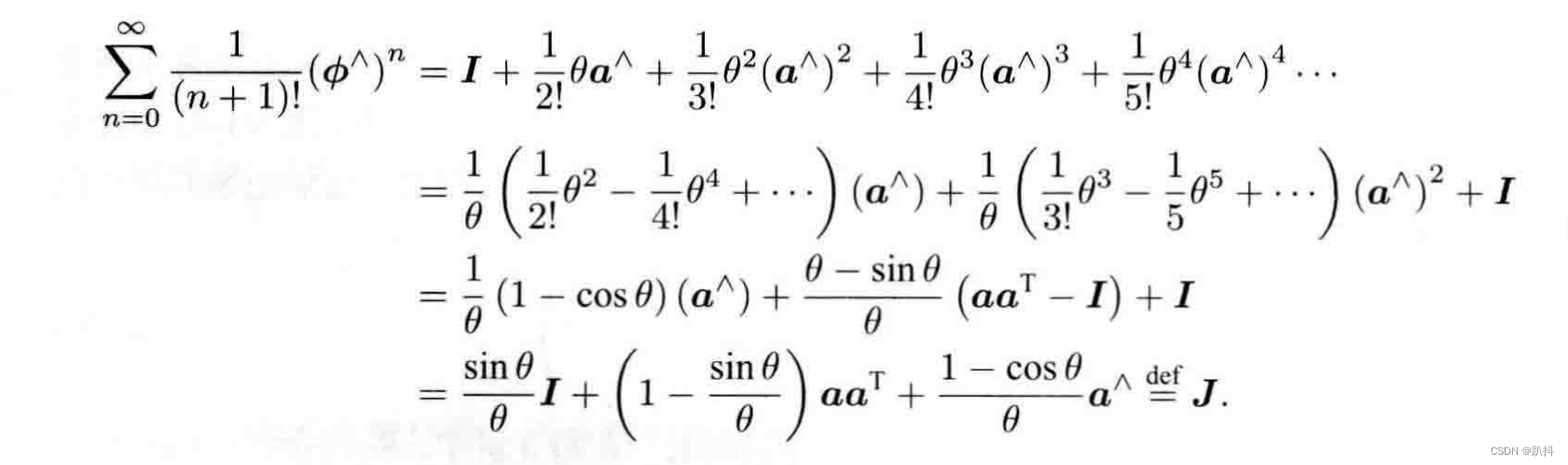
从结果上来看，ξ的指数映射左上角的R是我们熟知的SO(3)中的元素，与se(3)中的旋转部分φ。而右上角的J由上面的推导给出：

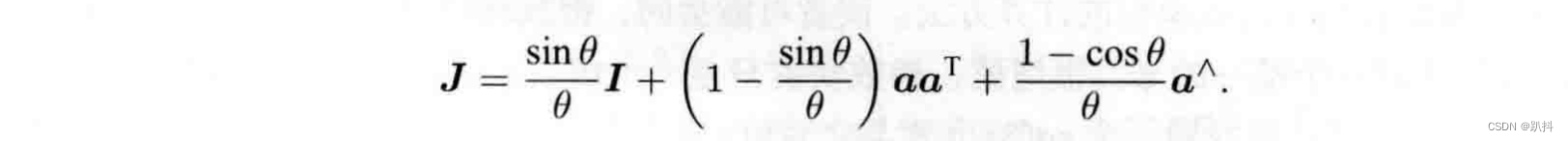
该式与罗德里格斯公式有点相似，但不完全一样。我们看到，平移部分经过指数映射之后，发生了一次以J为系数矩阵的线性变换。

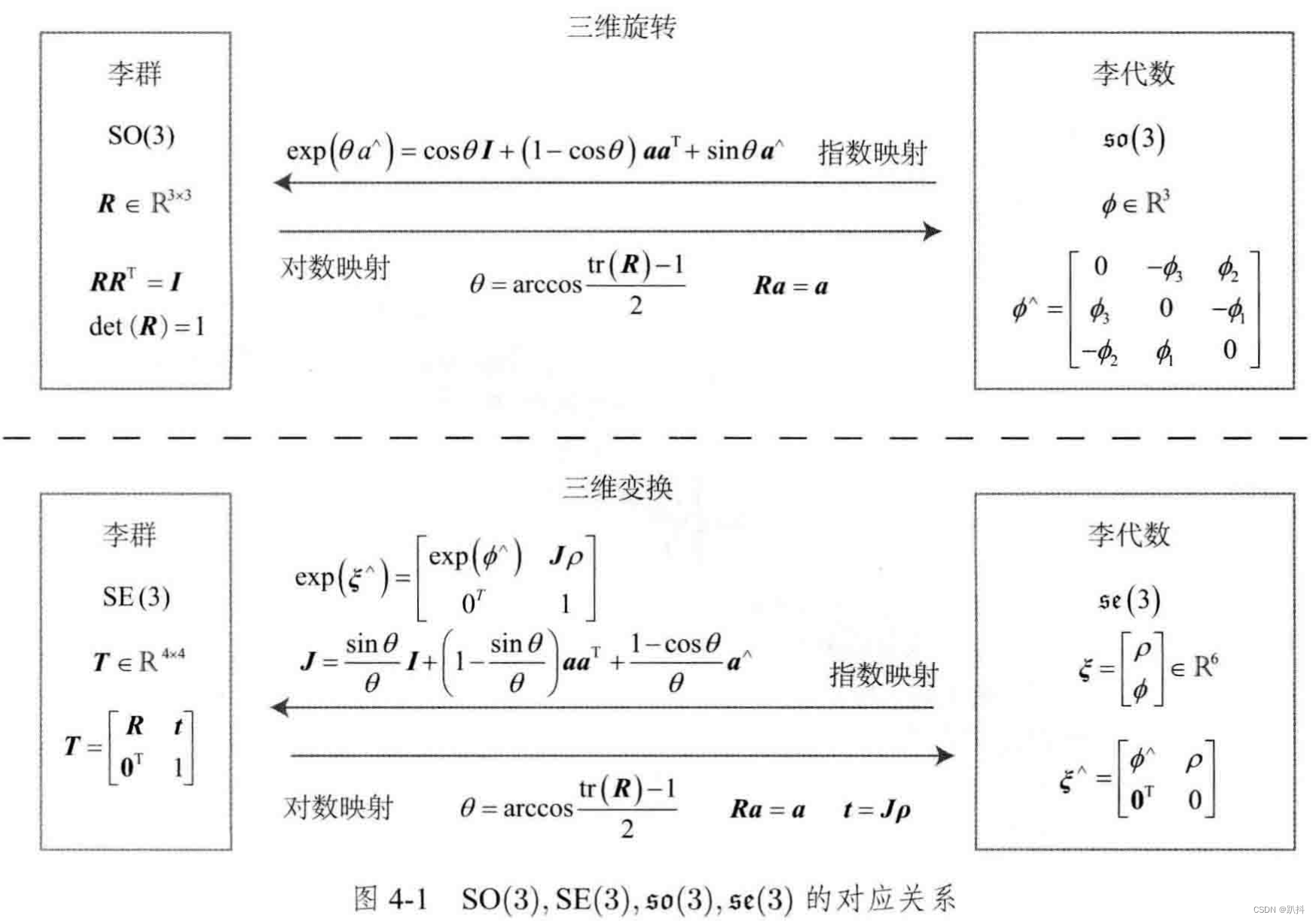
总结